	Главная \| Случайная страница \| Контакты \| Мы поможем в написании вашей работы!

Другие функции MATLAB. Основы численного расчета на matlab

⇐ Предыдущая 1 2 345 Следующая ⇒

calendar

Функция calendar выводит в командное окно календарь на текущий месяц в виде таблицы из семи столбцов.

>> calendar

Apr 2005

S M Tu W Th F S

0 0 0 0 0 1 2

3 4 5 6 7 8 9

10 11 12 13 14 15 16

17 18 19 20 21 22 23

24 25 26 27 28 29 30

0 0 0 0 0 0 0

Чтобы отобразить календарь какого-либо другого месяца и года, нужно задать функцию

calendar с двумя аргументами (первый из них будет означать год, а второй- номер месяца). Например, отобразим календарь на март 2005 года.

calendar(2005,3)

Mar 2005

S M Tu W Th F S

0 0 1 2 3 4 5

6 7 8 9 10 11 12

13 14 15 16 17 18 19

20 21 22 23 24 25 26

27 28 29 30 31 0 0

0 0 0 0 0 0 0

diap

Создает массив

Пример, создающий одномерный массив чисел в диапазоне от 0 до 10

diap=0:0.1:10

help

Полный список операторов можно получить, используя команду help ops. Постепенно мы рассмотрим все операторы системы MATLAB и обсудим особенности их применения. А пока приведем только часть полного списка операторов, содержащую арифметические операторы:

>> help ops

Plus	Plus	+
Uplus	Unary plus	+
Minus	Minus	-
Umlnus	Unary minus	-
Mtimes	Matrix multiply	*
times	Array multiply	*
mpower	Matrix power	^
poWer	Array power	.^
mldivide	Backslash or left matrix divide	\
mrdivide	Slash or right matrix divide	/
Idivide	Left array divide	.\
rdivide	Right array divide	./
kron	Kronecker tensor product	kron

Со списком элементарных функций можно ознакомиться, выполнив команду help elfun,

а со списком специальных функций – с помощью команды help specfun.

Функция eval ('выражение') интерпретирует и вычисляет текстовую строку, которая может содержать либо арифметическое выражение, либо инструкцию, либо обращение к функции

Примеры

Вычислим текущее время t:

format rational

eval('t = clock')

t = 1997 12 7 17 24 241/100

Следующий программный код позволяет сформировать матрицу Гильберта порядка n:

t = '1/(i + j-1)';

n = 4;

for i = 1:n

for j = 1:n

G(i, j) = eval(t);

end

format rational

G =

1 1/2 1/3 1/4

1/2 1/3 1/4 1/5

1/3 1/4 1/5 1/6

1/4 1/5 1/6 1/7

intersect

intersect - пересечение множеств для двух векторов а и b, т. е., общие элементы векторов а и b. Результирующий вектор отсортирован по возрастанию.

a=[1 2 3 4]

b=[3 4 5]

Ans=[3 4]

setdiff

setdiff-разность множеств т. е., те элементы вектора а, которые не содержатся в векторе b. Результирующий вектор сортируется по возрастанию

a=[1 2 3 4]

b=[3 4 5]

setdiff(a,b)

setdiff(b,a)

ans=[1 2]

ans=[5]

union - объединение множеств

union(a, b)

a=[1 2 3 4]

b=[3 4 5]

ans=[1 2 3 4 5]

unique - удаление из множеств одинаковых элементов

unique[1 2 3 4 5 2 4]

ans=[1 2 3 4 5]

Основы численного расчета на matlab

>> x=0:0.5:50

x =

Columns 1 through 7

0 0.5000 1.0000 1.5000 2.0000 2.5000 3.0000

Columns 8 through 14

3.5000 4.0000 4.5000 5.0000 5.5000 6.0000 6.5000

Columns 15 through 21

7.0000 7.5000 8.0000 8.5000 9.0000 9.5000 10.0000

Columns 22 through 28

10.5000 11.0000 11.5000 12.0000 12.5000 13.0000 13.5000

Columns 29 through 35

14.0000 14.5000 15.0000 15.5000 16.0000 16.5000 17.0000

Columns 36 through 42

17.5000 18.0000 18.5000 19.0000 19.5000 20.0000 20.5000

Columns 43 through 49

21.0000 21.5000 22.0000 22.5000 23.0000 23.5000 24.0000

Columns 50 through 56

24.5000 25.0000 25.5000 26.0000 26.5000 27.0000 27.5000

Columns 57 through 63

28.0000 28.5000 29.0000 29.5000 30.0000 30.5000 31.0000

Columns 64 through 70

31.5000 32.0000 32.5000 33.0000 33.5000 34.0000 34.5000

Columns 71 through 77

35.0000 35.5000 36.0000 36.5000 37.0000 37.5000 38.0000

Columns 78 through 84

38.5000 39.0000 39.5000 40.0000 40.5000 41.0000 41.5000

Columns 85 through 91

42.0000 42.5000 43.0000 43.5000 44.0000 44.5000 45.0000

Columns 92 through 98

45.5000 46.0000 46.5000 47.0000 47.5000 48.0000 48.5000

Columns 99 through 101

49.0000 49.5000 50.0000

>> y=sin(x)

y =

Columns 1 through 7

0 0.4794 0.8415 0.9975 0.9093 0.5985 0.1411

Columns 8 through 14

-0.3508 -0.7568 -0.9775 -0.9589 -0.7055 -0.2794 0.2151

Columns 15 through 21

0.6570 0.9380 0.9894 0.7985 0.4121 -0.0752 -0.5440

Columns 22 through 28

-0.8797 -1.0000 -0.8755 -0.5366 -0.0663 0.4202 0.8038

Columns 29 through 35

0.9906 0.9349 0.6503 0.2065 -0.2879 -0.7118 -0.9614

Columns 36 through 42

-0.9756 -0.7510 -0.3425 0.1499 0.6055 0.9129 0.9968

Columns 43 through 49

0.8367 0.4716 -0.0089 -0.4872 -0.8462 -0.9981 -0.9056

Columns 50 through 56

-0.5914 -0.1324 0.3591 0.7626 0.9794 0.9564 0.6992

Columns 57 through 63

0.2709 -0.2238 -0.6636 -0.9410 -0.9880 -0.7931 -0.4040

Columns 64 through 70

0.0840 0.5514 0.8839 0.9999 0.8711 0.5291 0.0575

Columns 71 through 77

-0.4282 -0.8090 -0.9918 -0.9317 -0.6435 -0.1978 0.2964

Columns 78 through 84

0.7180 0.9638 0.9736 0.7451 0.3342 -0.1586 -0.6126

Columns 85 through 91

-0.9165 -0.9961 -0.8318 -0.4638 0.0177 0.4949 0.8509

Columns 92 through 98

0.9986 0.9018 0.5842 0.1236 -0.3673 -0.7683 -0.9811

Columns 99 through 101

-0.9538 -0.6929 -0.2624

>> plot(x,y)

b) >> x=0:0.5:50

x =

Columns 1 through 7

0 0.5000 1.0000 1.5000 2.0000 2.5000 3.0000

Columns 8 through 14

3.5000 4.0000 4.5000 5.0000 5.5000 6.0000 6.5000

Columns 15 through 21

7.0000 7.5000 8.0000 8.5000 9.0000 9.5000 10.0000

Columns 22 through 28

10.5000 11.0000 11.5000 12.0000 12.5000 13.0000 13.5000

Columns 29 through 35

14.0000 14.5000 15.0000 15.5000 16.0000 16.5000 17.0000

Columns 36 through 42

17.5000 18.0000 18.5000 19.0000 19.5000 20.0000 20.5000

Columns 43 through 49

21.0000 21.5000 22.0000 22.5000 23.0000 23.5000 24.0000

Columns 50 through 56

24.5000 25.0000 25.5000 26.0000 26.5000 27.0000 27.5000

Columns 57 through 63

28.0000 28.5000 29.0000 29.5000 30.0000 30.5000 31.0000

Columns 64 through 70

31.5000 32.0000 32.5000 33.0000 33.5000 34.0000 34.5000

Columns 71 through 77

35.0000 35.5000 36.0000 36.5000 37.0000 37.5000 38.0000

Columns 78 through 84

38.5000 39.0000 39.5000 40.0000 40.5000 41.0000 41.5000

Columns 85 through 91

42.0000 42.5000 43.0000 43.5000 44.0000 44.5000 45.0000

Columns 92 through 98

45.5000 46.0000 46.5000 47.0000 47.5000 48.0000 48.5000

Columns 99 through 101

49.0000 49.5000 50.0000

>> y=sin(x)

y =

Columns 1 through 7

0 0.4794 0.8415 0.9975 0.9093 0.5985 0.1411

Columns 8 through 14

-0.3508 -0.7568 -0.9775 -0.9589 -0.7055 -0.2794 0.2151

Columns 15 through 21

0.6570 0.9380 0.9894 0.7985 0.4121 -0.0752 -0.5440

Columns 22 through 28

-0.8797 -1.0000 -0.8755 -0.5366 -0.0663 0.4202 0.8038

Columns 29 through 35

0.9906 0.9349 0.6503 0.2065 -0.2879 -0.7118 -0.9614

Columns 36 through 42

-0.9756 -0.7510 -0.3425 0.1499 0.6055 0.9129 0.9968

Columns 43 through 49

0.8367 0.4716 -0.0089 -0.4872 -0.8462 -0.9981 -0.9056

Columns 50 through 56

-0.5914 -0.1324 0.3591 0.7626 0.9794 0.9564 0.6992

Columns 57 through 63

0.2709 -0.2238 -0.6636 -0.9410 -0.9880 -0.7931 -0.4040

Columns 64 through 70

0.0840 0.5514 0.8839 0.9999 0.8711 0.5291 0.0575

Columns 71 through 77

-0.4282 -0.8090 -0.9918 -0.9317 -0.6435 -0.1978 0.2964

Columns 78 through 84

0.7180 0.9638 0.9736 0.7451 0.3342 -0.1586 -0.6126

Columns 85 through 91

-0.9165 -0.9961 -0.8318 -0.4638 0.0177 0.4949 0.8509

Columns 92 through 98

0.9986 0.9018 0.5842 0.1236 -0.3673 -0.7683 -0.9811

Columns 99 through 101

-0.9538 -0.6929 -0.2624

>> x1=(0:0.1:2)*pi/50

x1 =

Columns 1 through 7

0 0.0063 0.0126 0.0188 0.0251 0.0314 0.0377

Columns 8 through 14

0.0440 0.0503 0.0565 0.0628 0.0691 0.0754 0.0817

Columns 15 through 21

0.0880 0.0942 0.1005 0.1068 0.1131 0.1194 0.1257

>> y1=380*sin(50*x1)

y1 =

Columns 1 through 7

0 117.4265 223.3584 307.4265 361.4015 380.0000 361.4015

Columns 8 through 14

307.4265 223.3584 117.4265 -0.0000 -117.4265 -223.3584 -307.4265

Columns 15 through 21

-361.4015 -380.0000 -361.4015 -307.4265 -223.3584 -117.4265 0.0000

>> y2=380*sin(50*x1-2*pi/3)

y2 =

Columns 1 through 7

-329.0897 -371.6961 -377.9183 -347.1473 -282.3950 -190.0000 -79.0064

Columns 8 through 14

39.7208 154.5599 254.2696 329.0897 371.6961 377.9183 347.1473

Columns 15 through 21

282.3950 190.0000 79.0064 -39.7208 -154.5599 -254.2696 -329.0897

>> y3=380*sin(50*x1-4*pi/3)

y3 =

Columns 1 through 7

329.0897 254.2696 154.5599 39.7208 -79.0064 -190.0000 -282.3950

Columns 8 through 14

-347.1473 -377.9183 -371.6961 -329.0897 -254.2696 -154.5599 -39.7208

Columns 15 through 21

79.0064 190.0000 282.3950 347.1473 377.9183 371.6961 329.0897

>> plot(x1,y1,x1,y2,x1,y3)

*)>> plot(x1,y1,'m-',x1,y2,'k--',x1,y3,'c-.')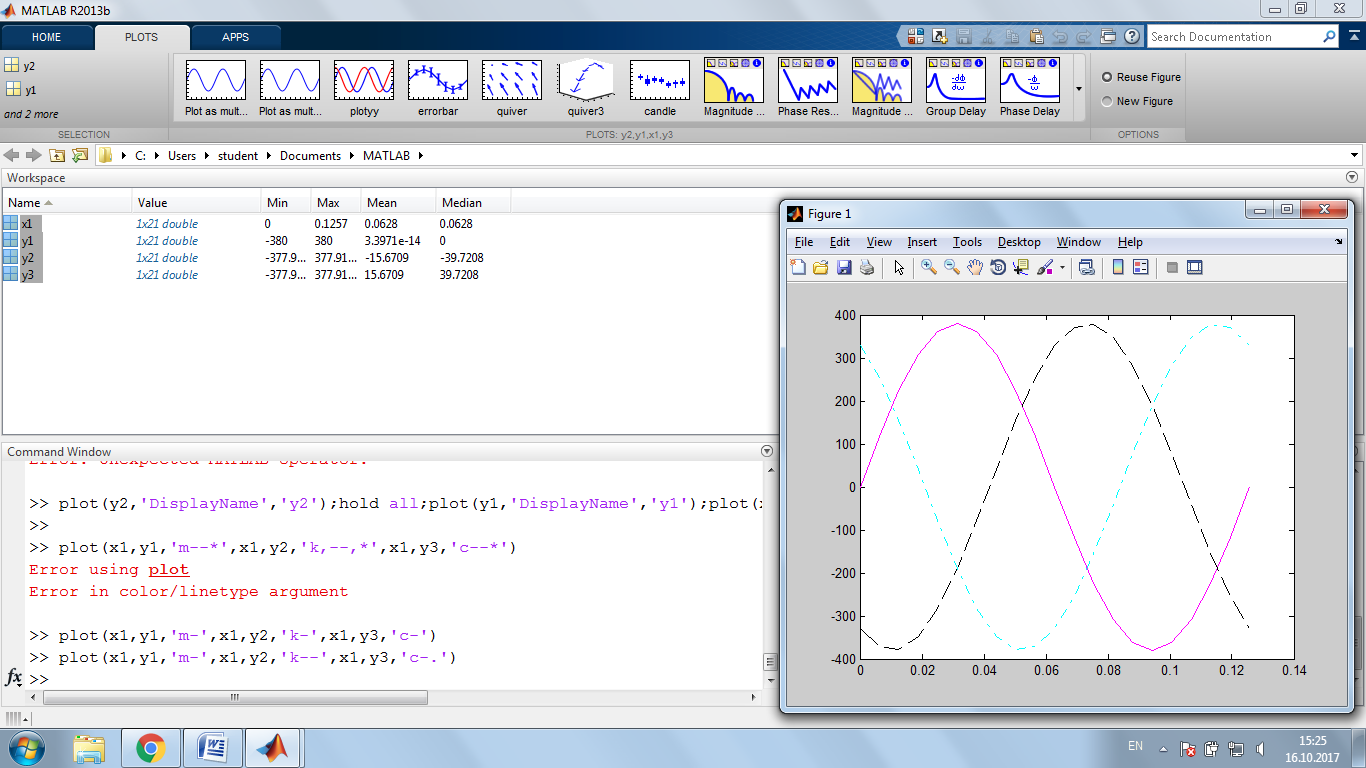

>> for i=1:10

pause(1)

i=i+0

end

i =

b) >> n=5;

>> A=ones(n,n);

>> B=2*ones(n,n);

>> tic

>> for i=1:length(A)

for j=1:length(A)

for k=1:length(A)

D(k)=A(i,k)*B(k,j);

end

C(i,j)=sum(D(:));

end

>> C

C =

10 10 10 10 10

>> toc

Elapsed time is 154.230555 seconds.

>> tic

>> for i=1:length(A)

for j=1:length(A)

C1(i,j)=A(i,:)*B(:,j);

end

>> C1

C1 =

10 10 10 10 10

>> toc

Elapsed time is 99.967373 seconds.

>> tic

>> C2=A*B

C2 =

10 10 10 10 10

>> toc

Elapsed time is 12.824037 seconds.

4. >> x=0:0.01:2*pi;

>> y=sin(x);

>> for i=1:length(x)

plot(x(i),y(i),'linewidth',4,'color',[0 1 0])

hold on

xlim([0 2*pi])

ylim([-1.1 1.1])

pause(0.01)

end

>> grid('minor')

>> xlabel('x')

>> ylabel('y')

>> title('ex10a')

⇐ Предыдущая 1 2 345 Следующая ⇒

Дата публикования: 2023-10-24; Прочитано: 734 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!

studopedia.org - Студопедия.Орг - 2014-2024 год. Студопедия не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования (0.057 с)...