Пример решения работы. Данное пособие написано для того, чтобы помочь студентам, обучающимся на факультете заочного и дистанционного обучения по направлению «эксплуатация

Введение

Данное пособие написано для того, чтобы помочь студентам, обучающимся на факультете заочного и дистанционного обучения по направлению «эксплуатация транспортно-технологических машин и комплексов» и профилю «автомобили и автомобильное хозяйство», в освоении тех разделов математики, которые изучаются в первом семестре, а также помочь в выполнении контрольных работ по математике по соответствующим темам: № 1,2, 3.

В пособии имеется необходимый теоретический материал, пример выполнения соответствующей контрольной работы и задания для самостоятельного выполнения в десяти вариантах. Номер варианта определяется по последней цифре зачётной книжки (шифра).

Работу следует выполнять в тонкой ученической тетради в клетку. Выполненную работу следует снабдить титульным листом, образец которого можно найти на доске объявлений у деканата.

Поскольку пособие содержит достаточно большой теоретический материал, полезно сохранить его до конца обучения в вузе, так как он может быть востребован при дальнейшем изучении математики и других дисциплин.

Раздел 1. Контрольная работа по математике №1

Элементы векторной алгебры и аналитической геометрии

Теоретический материал для данной контрольной работы был представлен на установочных занятиях. При возникновении каких-либо вопросов следует обращаться к нему.

Пример решения работы

Задание №1. Даны два вектора и . Найти их длины , , сумму , линейную комбинацию , скалярное произведение , векторное произведение , угол (в градусах) между векторами .

Решение

1) Длины векторов равны:

; .

2) Найдем сумму и линейную комбинацию :

;

.

3) Скалярное произведение равно:

.

4) Векторное произведение равно:

.

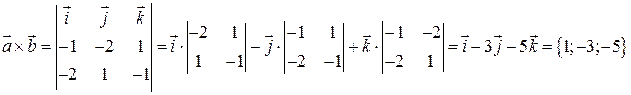5) Из определения скалярного произведения:

.

В условиях данной задачи:

.

Тогда .

Ответ: 1) ;

2) ; .

3) ;

4) ;

5) .

Задание №2. Найти объем, площадь основания и высоту пирамиды с вершинами в точках , , , , 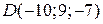опущенную из вершины 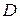на грань .

Решение

Из формулы выразим высоту .

Для решения задачи введем векторы: 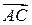, , , при этом , , .

1) Объем пирамиды находится как модуль смешанного произведения векторов , , :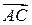

.

2) Площадь основания находится по формуле:

,

,

3) Длина высоты, опущенной из вершины 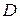на грань , находится из формулы . Получим:

.

Ответ: ; ; .

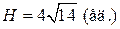Задание №3. Даны вершины треугольника : , , 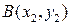. Найти:

а) уравнение стороны ;

б) уравнение высоты ;

в) уравнение медианы ;

г) точку пересечения медианы и высоты ;

д) уравнение прямой, проходящей через вершину , параллельно ;

е) расстояние от точки до прямой ;

ж) сделать чертеж.

Для разбора решения задачи отметим на координатной плоскости точки: , , .

Решение

а) Для нахождения уравнения стороны воспользуемся уравнением прямой, проходящей через две заданные точки:

:


().

б) Для составления уравнения высоты воспользуемся условием перпендикулярности прямых и (), а также уравнением прямой, проходящей через данную точку с данным угловым коэффициентом:

.

Итак, : ,

следовательно, . Тогда по условию

.

Уравнение примет вид:

: ().

в) Для составления уравнения медианы найдем сначала координаты точки - середины отрезка :

; ; .

Тогда : ().

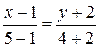
г) Для нахождения координат точки - пересечения медианы и высоты составим и решим систему уравнений:

; .

Итак, .

д) Уравнение прямой 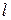, проходящей через точку параллельно , будем искать в виде: .

Так как 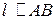, то (угловые коэффициенты у параллельных прямых равны).

(смотри пункт б)). Но тогда .

Итак, или .

е) Расстояние от точки до прямой может быть найдено по формуле:

, при этом, : , а, значит

; ; ; ; .

Следовательно, .

Ответ: а) (); б) (); в) (); г) ; д) ; е) .

Задание №4. Найти угол (в градусах) между плоскостями и .

Решение

Величина угла между плоскостями, заданными уравнениями

и

вычисляется на основании формулы:

.

А, значит, в условиях данной задачи, когда ; ; ; ; ; , имеем:

.

Итак, .

Ответ: .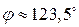

Задание №5. Найти точку пересечения прямой и плоскости .

Решение

Для того, чтобы найти точку пересечения прямой и плоскости нужно решить совместно их уравнения, для чего следует воспользоваться параметрическими уравнениями прямой в пространстве.

Параметрические уравнения данной прямой имеют вид: .

Подставив в уравнение плоскости найдем - то значение параметра, при котором происходит пересечение:

;

А, значит, ; ; .

Итак, точка пересечения данной прямой и данной плоскости - .

Ответ: .