Розривні функції. Види розривів

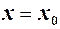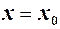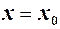Якщо в якійсь точці для функції не виконується хоча б одна із умов неперервності, тобто якщо в точці функція невизначена, або неіснує границя , або при довільному прямуванні , хоча вирази і існують, то при функція розривна. Точка 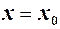називається точкою розриву функції.

Розрізняють такі три види розривів:

1) усувний розрив;

2) розрив І-го роду або скінченний розрив;

3) розрив ІІ-го роду або нескінченний розрив.

Якщо функція в деякому околі точки 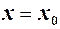визначена і її односторонні границі збігаються, тобто

= ,

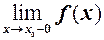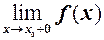а в самій точці 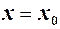функція невизначена, то в цій точці має усувний розрив. Цей розрив можна усунути, приписавши функції значення, що збігається з односторонніми границями і взявши

= .

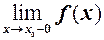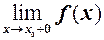Наприклад, функція неперервна на всьому інтервалі від –¥ до +¥, крім точки 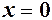. В точці 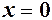функція розривна.

Розглянемо нову функцію , таку, що якщо

, а при 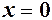покладемо

Побудована таким чином функція

є неперервною для (див. рис. 29), тобто розрив усунули.

Рис. 29.

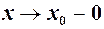Якщо односторонні границі функції скінченні при і , то функція в точці 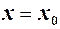має розрив І-го роду або скінченний розрив.

Наприклад, функція при дорівнює при а при функція невизначена, тоді

отже має розрив І-го роду (див. рис. 30).

Рис. 30.

Стрибком функції називається величина

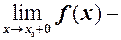
У точках неперервності стрибок , для розривів І-го роду він скінченний. Для розглянутого на рис. 30 графіка стрибок .

Якщо хоча б одна з односторонніх границь функції в точці 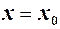є нескінченною або не існує, тоді функція в точці 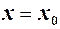має розрив ІІ-го роду або нескінченний розрив.

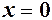Наприклад, в точці невизначена, , а 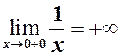, тобто односторонні границі нескінченні, тому тут розрив ІІ-го роду (див. рис.31).

Так само точка 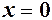є точкою розриву ІІ-го роду для розглянутої раніше функції , бо не існує.