Глава 3. Количественная оценка информации 6 страница

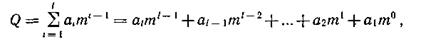
где i — номер разряда данного числа; l — количество разрядов; a_i — множитель, принимающий любые целочисленные значения в пределах от 0 до m-1 и показывающий, сколько единиц ί-го разряда содержится в числе.

Чем больше основание системы счисления, тем меньшее число разрядов требуется для представления данного числа, а следовательно, и меньшее время для его передачи.

Однако с ростом основания существенно повышаются требования к линии связи и аппаратуре создания и распознавания элементарных сигналов, соответствующих различным символам. Логические элементы вычислительных устройств в этом случае должны иметь большее число устойчивых состояний.

Учитывая оба обстоятельства, целесообразно выбрать систему, обеспечивающую минимум произведения количества различных символов m на количество разрядов l для выражения любого числа. Найдем этот минимум по графику на рис. 5.1, где показана связь между величинами m и l при воспроизведении определенного достаточно большого числа Q (Q ≈ 60 000).

Из графика следует, что наиболее эффективной системой является троичная. Незначительно уступают ей двоичная и четверичная. Системы с основанием 10 и более существенно менее эффективны. Сравнивая эти системы с точки зрения удобства физической реализации соответствующих им логических элементов и простоты выполнения в них арифметических и логических действий, предпочтение необходимо отдать двоичной системе. Действительно, логические элементы, соответствующие этой системе, должны иметь всего два устойчивых состояния. Задача различения сигналов сводится в этом случае к задаче обнаружения (есть импульс или нет импульса), что значительно проще.

Арифметические и логические действия также наиболее просто осуществляются в двоичной системе. В таблицы сложения, вычитания и умножения входит всего по четыре равенства:

Правила Правила Правила

сложения: вычитания: умножения

0 + 0 = 0	0 – 0 = 0	0 · 0 = 0
0 + 1 = 1	1 – 0 = 1	0 · 1 = 0
1 + 0 = 1	1 – 1 = 0	1 · 0 = 0
1 + 1 = 1	0 – 1 = 1	1 · 1 = 1

Наиболее распространенная при кодировании и декодировании логическая операция — сложение по модулю. В двоичной системе она также наиболее проста и определяется равенствами:

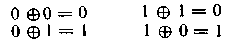
Алгоритм перевода из двоичной в привычную для человека десятичную систему несложен. Пересчет начинается со старшего разряда. Если в следующем разделе стоит 0, то цифра предыдущего (высшего) разряда удваивается. Если же в следующем разряде единица, то после удвоения предыдущего разряда результат увеличивается на единицу.

Пример 5.1. Найдем десятичный эквивалент двоичного числа 1001. После первой единицы слева стоит 0. Удваиваем эту единицу. Получаем число 2. Цифрой следующего младшего разряда также является 0. Удваивая число 2, получаем 4. В самом младшем разряде стоит единица. Удваивая число 4 и прибавляя 1, окончательно получаем 9.

Итак, для передачи и проведения логических и арифметических операций наиболее целесообразен двоичный код. Однако он неудобен при вводе и выводе информации, так как трудно оперировать с непривычными двоичными числами. Кроме того, запись таких чисел на бумаге оказывается слишком громоздкой. Поэтому, помимо двоичной, получили распространение системы, которые, с одной стороны, легко сводятся как к двоичной, так и к десятичной системе, а с другой стороны, дают более компактную запись. К таким системам относятся восьмеричная, шестнадцатеричная и двоично-десятичная.

В восьмеричной системе для записи всех возможных чисел используется восемь цифр от 0 до 7 включительно. Перевод чисел из восьмеричной системы в двоичную крайне прост и сводится к замене каждой восьмеричной цифры равным ей трехразрядным числом. Например, для восьмеричного числа 754 получаем:

7 4 5

111 100 101

Поскольку в восьмеричной системе числа выражаются короче, чем в двоичной, она широко используется как вспомогательная система при программировании.

Чтобы сохранить преимущества двоичной системы и удобство десятичной системы, используют двоично-десятичные коды. В таком коде каждую цифру десятичного числа записывают в виде четырехразрядного двоичного числа (тетрады). С помощью четырех разрядов можно образовать 16 различных комбинаций, из которых любые 10 могут составить двоично-десятичный код. Наиболее целесообразным является код 8-4-2-1 (табл. 5.1). Этот код относится к числу взвешенных кодов. Цифры в названии кода означают вес единиц в соответствующих двоичных разрядах. Двоично-десятичный код обычно используется как промежуточный при введении в вычислительную машину данных, представленных в десятичном коде.

Таблица 5.1

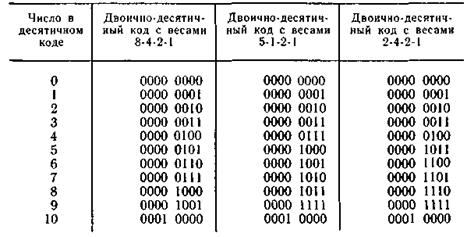
В табл. 5.1 представлены два других двоично-десятичных кода с весами 5-1-2-1 и 2-4-2-1, которые широко используются при поразрядном уравновешивании в цифровых измерительных приборах.

Среди кодов, отходящих от систем счисления, большое практическое значение имеют такие, у которых при переходе от одного числа к другому изменение происходит только в одном разряде.

Наибольшее распространение получил код Грея, часто называемый циклическим или рефлексно - двоичным. Код Грея используется в технике аналого-цифрового преобразования, где он позволяет свести к единице младшего разряда ошибку неоднозначности при считывании. Комбинации кода Грея, соответствующие десятичным числам от 0 до 15, приведены в табл. 5.2.

Таблица 5.2

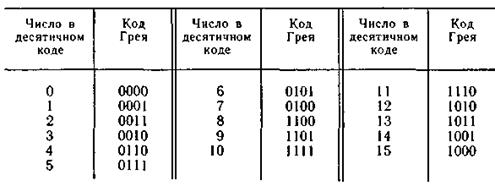
Правила перевода числа из кода Грея в обычный двоичный сводятся к следующему: первая единица со стороны старших разрядов остается без изменения, последующие цифры (0 и 1) остаются без изменения, если число единиц, им предшествующих, четно, инвертируются, если число единиц нечетно.

Пример 5.2. Выразим число 1010, записанное в коде Грея, в обычном двоичном коде.

Первую единицу слева переписываем. Следующая цифра будет единицей, так как в этом разряде кода Грея стоит нуль и впереди только одна единица. Далее необходимо записать нуль, так как в следующем разряде исходного числа стоит единица и впереди снова имеется только одна единица. Поскольку перед последней цифрой числа в коде Грея стоят две единицы, то она должна остаться неизменной, т. е. нулем. Таким образом, числу 1010 в коде Грея соответствует обычное двоичное число 1100.

§ 5.2. ТЕХНИЧЕСКИЕ СРЕДСТВА ПРЕДСТАВЛЕНИЯ ИНФОРМАЦИИ В ЦИФРОВОЙ ФОРМЕ

Разновидности преобразователей. Устройства, позволяющие заменять непрерывную последовательность значений аналоговой величины конечным числом дискретных значений и представлять их в заданном коде, получили название аналого-кодовых преобразователей. Кодовые эквиваленты аналоговой величины могут быть представлены комбинациями состояний оптических, электромеханических, электронных и других элементов, а также параллельными или последовательными во времени комбинациями электрических импульсов.

В случае необходимости обработки информации посредством цифровых вычислительных машин, как правило, используются представления в двоичном коде.

В аналого-кодовых преобразователях, которые должны выдавать кодовые эквиваленты на систему цифровой индикации или на регистрирующее устройство, непосредственно используемое человеком, целесообразно применять представления в десятичном коде.

Аналого-кодовые преобразователи можно классифицировать по многим существенным признакам. Важнейшими из них являются принцип работы измерительной части преобразователя и способ получения цифрового эквивалента.

В принципе возможно непосредственное преобразование различных физических величин в цифровую форму. Такие преобразователи называют кодовыми датчиками. Примером могут служить цифровые преобразователи угла поворота вала (фазовые преобразователи угла).

Однако в настоящее время более рационально преобразовывать различные по физической природе сигналы в электрические, а затем представлять их в цифровой форме посредством преобразователей напряжение — код. Под термином «аналого-цифровой преобразователь» (АЦП) в первую очередь подразумевают именно такой преобразователь (напряжение — код).

Кодовые датчики геометрических координат. В таких датчиках в процессе преобразования определяется, какому месту на заранее заданном геометрическом пространственном рисунке (кодирующей маске) соответствует данный входной сигнал.

Кодирующую маску выполняют в виде прямоугольной пластины или диска. В последнем случае знаки разрядов нанесены на концентрические дорожки, каждая из которых соответствует определенному разряду двоичного числа. Внешняя дорожка диска соответствует низшему разряду (рис. 5.2). Итак, каждому дискретному значению угла ставится в соответствие вполне определенная неповторяющаяся комбинация сегментов двух типов, соответствующих 1 и 0.

Разрешающая способность диска определяется числом всех сегментов дорожки младшего разряда. Она может быть повышена применением системы нескольких дисков, соединенных с помощью понижающего редуктора. В зависимости от способа съема кода (контактный, фотоэлектрический, магнитный и т. д.) сегменты, составляющие рисунок кода, выполняют проводящими и непроводящими, прозрачными и непрозрачными, магнитопроницаемыми и магнитонепроницаемыми и т. д.

Для считывания с каждого из разрядов установлены чувствительные элементы: щетки, фотоэлементы, индуктивные катушки и т. д.

При опросе чувствительных элементов получаем комбинацию электрических сигналов, представляющую в выбранном коде число, соответствующее данному углу поворота. К сожалению, при использовании масок с обычным двоичным кодом в местах, где одновременно изменяется состояние нескольких чувствительных элементов, при считывании могут возникать значительные погрешности. Например, если чувствительные элементы располагаются на границе между числом 7 (0111) и 8 (1000), то преобразователь может выдать на выходе любое число от 0 до 15. Это, конечно, недопустимо.

Указанный недостаток может быть устранен как за счет увеличения числа чувствительных элементов (метод сдвоенных щеток, метод Баркера [26]), так и путем использования масок с кодами, у которых при последовательном переходе от числа к числу изменяется только один разряд. Наиболее часто применяется код Грея. Кодирующая маска с кодом Грея изображена на рис. 5.3.

Нетрудно убедиться, что каждое последующее число отличается от предыдущего только в одном разряде, поэтому погрешность при считывании не может превосходить единицы младшего разряда независимо от того, в каком разряде имела место неопределенность.

Использование этого способа приводит к необходимости иметь дополнительный преобразователь для представления полученных в коде Грея чисел в обыкновенном двоичном коде.

Кодовый диск, чувствительные элементы и преобразователь кода конструктивно объединены в одном корпусе. Датчики отличаются высоким быстродействием и большой точностью. У лучших двухотсчетных фазовых преобразователей угла погрешность составляет доли секунды.

Аналого-цифровые преобразователи. Современные АЦП строят на основе серийно выпускаемых отечественной промышленностью интегральных схем, номенклатура которых достаточно высока. В нее входят операционные усилители, органы сравнения (компараторы напряжения), источники опорного напряжения, коммутаторы, цифроаналоговые преобразователи, устройства запоминания и другие функциональные элементы и узлы. Поскольку степень интеграции схем постоянно растет, количество интегральных схем, необходимых для реализации конкретного АЦП, уменьшается.

Имеются образцы АЦП, выполненных на одном кристалле. Успехи в технологии изготовления интегральных схем способствовали увеличению быстродействия, повышению надежности и снижению стоимости АЦП.

По способу получения цифрового эквивалента все разнообразие существующих преобразователей может быть разбито на три основные группы: преобразователи последовательного счета, преобразователи поразрядного уравновешивания, преобразователи считывания.

Аналого-цифровые преобразователи последовательного счета. В преобразователях этого класса непрерывная величина электрического тока или напряжения предва-тельно преобразуется в импульсы, общее число которых соответствует ее значению. Эти импульсы передаются последовательно к двоичному или десятичному счетчику, где происходит их суммирование.

При заданном отнесенном к шкале шаге квантования преобразователя δ (%), число импульсов m_х, представляющих одно значение кодируемой величины u_х, может меняться в пределах

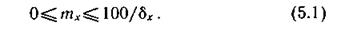
Если частота счетчика предельная f_{сч mах}, то время, требующееся на один цикл преобразования, равно

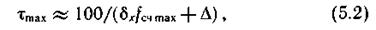
где Δ — время считывания цифрового эквивалента и сброса счетчика.

Отметим, что для преобразователя последовательного счета со следящим принципом измерения такое время потребуется только в случае резкого изменения кодируемой величины на полный диапазон преобразования.

Современные серии элементов допускают построение счетчиков с максимальной тактовой частотой по счетному входу до 50 МГц. Параллельное считывание и сброс счетчика можно выполнить за время, значительно меньшее 1 мкс. Следовательно, при относительном шаге квантования 0,1 % преобразователи последовательного счета в состоянии обеспечить число преобразований порядка 5·10⁴ в секунду. Точность преобразователя зависит от принципа работы его измерительной части.

Аналого-цифровые преобразователи последовательного счета выполняют на основе прямого, развертывающего или следящего измерительного преобразования.

Преобразователи с прямым измерительным преобразованием. Функциональная схема такого преобразователя приведена на рис. 5.4. Частота следования выходных импульсов управляемого генератора Ρ (u_х→f_x) линейно изменяется в зависимости от значения преобразуемого напряжения u_х.

В каждом цикле преобразования сигнал с генератора эталонных временных интервалов (ГЭВИ) на определенное время Т открывает схему совпадения И_т, пропуская импульсы в счетчик С_ч. Количество импульсов, зафиксированное счетчиком за время Т, пропорционально кодируемой величине u_х. По окончании сигнала, воздействующего на схему И_т, ГЭВИ выдает импульсы на считывание цифрового эквивалента Ζ и установку всех разрядов счетчика в исходное состояние (сброс). Далее процесс повторяется.

Основная трудность при реализации такого преобразователя заключается в создании генератора Ρ с достаточно линейной зависимостью частоты следования выходных импульсов от преобразуемого напряжения. Трудно добиться и его стабильности, особенно при изменении напряжения питания и температуры. Тем не менее в последнее время разработан ряд высокостабильных преобразователей напряжение — частота, позволивших снизить погрешность до 0,01 %.

Преобразователи с развертывающим измерительным преобразованием. Функциональная схема преобразователя изображена на рис. 5.5.

В начале каждого цикла преобразования запускается генератор ГКН линейно изменяющегося компенсирующего напряжения u_к. Одновременно сигнал с органа сравнения ОС открывает схему совпадения И, и импульсы высокостабильного генератора ГИ начинают поступать в счетчик С_ч. В момент компенсации, когда преобразуемое напряжение u_х сравнивается с компенсирующим напряжением u_к, состояние органа сравнения изменяется и доступ импульсов в счетчик прекращается. С выхода счетчика снимается цифровой эквивалент Ζ, соответствующий u_х.

Число импульсов, поступивших в счетчик, пропорционально преобразуемому напряжению u_х. Временная диаграмма работы преобразователя приведена на рис. 5.6.

По окончании цикла развертки компенсирующего напряжения с блока синхронизации БС поступают импульсы на считывание цифрового эквивалента и сброс счетчика. Далее процесс повторяется.

Блок синхронизации позволяет «привязать» момент начала развертки компенсирующего напряжения к одному из импульсов ГИ, что повышает точность преобразования (рис. 5.7, а). Действительно (рис. 5.7,6), при отсутствии синхронизации погрешность дискретизации может оказаться вдвое больше:

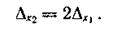
Блок синхронизации может представлять собой счетчик, который фиксирует число импульсов, соответствующее циклу преобразования, и запускает по окончании следования этого числа импульсов генератор компенсирующего напряжения.

Точность преобразования определяется характеристикой органа сравнения и линейностью компенсирующего напряжения. Обычно она достигает 0,1 %.

Более точными (до 0,005%) являются аналогичные преобразователи со ступенчато-линейным компенсирующим напряжением (рис. 5.8). Как правило, оно получается в результате суммирования коммутируемых по двоичному закону эталонных напряжений (или токов), амплитуды которых относятся друг к другу как целочисленные степени двух (1:2:4:8 и т. д.). Управление суммированием осуществляется импульсами, поступающими с двоичного счетчика, причем каждый раз, когда содержимое счетчика увеличивается на единицу, выходное напряжение возрастает на одну ступеньку [26].

Структурная схема преобразователя со ступенчато-линейным изменением компенсирующего напряжения показана на рис. 5.9. Импульсы от генератора ГИ поступают на триггеры T_Г1 — T_Г4, состояние которых определяет напряжение u_к на выходе источника ступенчатого компенсирующего напряжения ИСКН. Кодируемое напряжение u_х сравнивается со ступенчато-линейным u_к. В каждый момент времени на счетчике в двоичном коде фиксируется число ступеней компенсирующего на пряжения, т. е. цифровой эквивалент. В момент компенсации, когда ιι_x=ιι_κ, двоичное число на счетчике· является цифровым эквивалентом и для u_х.

Равенство напряжений u_х и u_к отмечается органом сравнения ОС, который и посылает импульс на считывание цифрового эквивалента Ζ со счетчика. Временные диаграммы работы преобразователя представлены на рис. 5.8, где показаны напряжения в точках а — г схемы рис. 5.9: интервал времени, пропорциональный u_х, обозначен t_x.

Преобразователи со следящим измерительным преобразованием. Преобразователь является цифровой следящей системой (рис. 5.10), в которой входное напряжение u_х сравнивается органом сравнения ОС с напряжением u_к, поступающим с источника линейно-ступенчатого компенсирующего напряжения ИСКН.

В зависимости от разности напряжений u_х — u_к происходит такое изменение кода в схеме управления источником, которое приводит к равенству этих напряжений в пределах заданной точности.

Орган сравнения воздействует на две схемы совпадения И, через которые импульсы генератора G поступают на входы реверсивного счетчика СТ: если 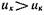, то

импульсы идут по каналу «+1», а если 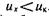, то по каналу «-1». При равенстве напряжений обе схемы И закрыты и импульсы на счетчик не поступают.

Минимальное напряжение срабатывания органа сравнения u_ср должно лежать в пределах 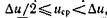где ∆u — напряжение одной ступеньки. При большей чувствительности значение младшего разряда цифрового эквивалента беспрерывно изменяется даже при постоянном значении u_х.

Отработка цифровых эквивалентов некоторой изменяющейся аналоговой величины u_х преобразователем со следящим уравновешиванием с момента его включения показана на рис. 5.11. Внизу записаны двоичные эквиваленты значений u_х на каждом такте. В схеме они представлены состоянием триггеров двоичного реверсивного счетчика СТ.

Для u_х, изменяющихся во времени плавно и с ограниченной скоростью, такой преобразователь, очевидно, обеспечит наибольшую скорость преобразования, так как время получения цифрового эквивалента уменьшается до одного такта.

Погрешность, как и в предыдущих схемах, зависит от стабильности органа сравнения и числа разрядов реверсивного двоичного счетчика. У лучших образцов она составляет 0,01—0,005 %.

Аналого-цифровые преобразователи поразрядного уравновешивания. Преобразователи, рассмотренные ранее, основаны на методе, при котором последовательно изменяется на единицу младшего разряда уровень компенсирующего напряжения и посредством органа сравнения каждый раз определяется, находится преобразуемая величина на данном уровне или нет.

Этот метод неэффективен с точки зрения числа операций сравнения (а следовательно, и быстродействия), необходимых для определения цифрового эквивалента резко изменяющейся величины u_х. Количество операций сравнения можно значительно сократить. Рассмотрим эту возможность.

Максимальное количество информации, которое можно получить в результате одной операции сравнения, равно 1 дв. ед. Для достижения этого значения каждую операцию сравнения необходимо проводить на таком уровне, чтобы вероятности обнаружения преобразуемой величины ниже и выше этого уровня были равны. Если вероятности всех значений преобразуемой величины одинаковы, то первую операцию сравнения при двоичном кодировании нужно провести на уровне u_{x max}/2. Цифровые эквиваленты напряжения u_х ниже этого уровня будут иметь в старшем разряде 0, а выше уровня — 1.

Следовательно, в результате операции сравнения будет определено значение старшего разряда цифрового эквивалента (0 или 1). Аналогично выбирают уровни сравнения для определения значений остальных разрядов. Каждый из них будет в 2 раза меньше предыдущего. Определение цифрового эквивалента производится поразрядно. При заданном относительном шаге квантования δ_x (%) число разрядов находим из соотношения

Значение i -го разряда определяют после проведения операции сравнения при поступлении с распределителя (i +1)-го импульса. На цикл преобразования, следовательно, требуется не менее (l +1) импульсов. Если используемые распределители работают по принципу пересчетных схем, то их предельную частоту снова обозначим через f с_{ч mах}. Тогда для аналого-цифровых преобразователей поразрядного уравновешивания максимально возможное число преобразований в секунду можно оценить по формуле

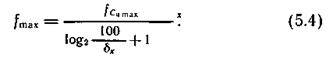
Приняв, как и ранее, δ_x = 0,1% и f с_{ч mах} = 5∙10⁷, максимальную частоту преобразователя получим равной 4,5·10⁶ Гц, что почти на два порядка превышает максимальную частоту преобразователей с линейно-ступенчатым компенсирующим напряжением.

Метод преобразования с поразрядным уравновешиванием может использоваться для получения цифровых эквивалентов u_х в любой системе счисления. В частности, в цифровых измерительных приборах широко применяется поразрядная отработка цифрового эквивалента u_х в десятичном и двоично-десятичном коде. Точность лучших преобразователей этого типа того же порядка, что и у преобразователей с линейно-ступенчатым уравновешиванием, т. е. до 0,005%. Конструктивно они несколько более сложны, но в ряде случаев незаменимы с точки зрения совмещения требований высокого быстродействия и высокой точности.

Типовая функциональная схема преобразователя поразрядного уравновешивания приведена на рис. 5.12. Уровни сравнения устанавливаются последовательным переключением триггеров двоичных разрядов, начиная со старшего Т г _п. Эталонное напряжение каждого уровня создается путем суммирования токов, пропорциональных весам разрядов, на резисторе r(r«R). Напряжение питания поступает от источника Ε.

Первый импульс с кольцевого распределителя КР переводит триггер Т г _п в состояние «1», а остальные через схемы ИЛИ устанавливает в «0». В замкнутом состоянии оказывается только ключ К_п. При этом компенсирующее напряжение и_к1 пропорционально весу старшего разряда (u_к1 = u_п). Если u_х<u_к1, то в цифровом эквиваленте u_х на месте старшего разряда должен стоять 0. В этом случае сигнал с органа сравнения ОС открывает элемент И и при поступлении второго импульса с распределителя триггер Т г _п сбрасывается в 0. Тем же импульсом в состояние «1» переводится триггер Т г _п-1. Уровень компенсирующего напряжения снижается вдвое (u_к2 = u_п-1= u_п/2)· Если теперь и_х>u_к2, то на месте этого разряда в цифровом эквиваленте u_х должна стоять 1. Знак выходного напряжения органа сравнения изменяется на противоположный, и элементы И запираются. Поэтому третий импульс, переключающий триггер Т г _п-2 на триггер Т г _п-1, не воздействует и последний остается в состоянии «T». Компенсирующее напряжение возрастает на u_п-2= u_п2^-2:

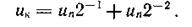
Если u_х<u_к3, то Т г _п-2 очередным импульсом сбрасывается в состояние «0», если u_х>u_к3, то T г _п-2 остается в состоянии «1». Аналогично отрабатываются значения всех остальных разрядов, причем значение младшего разряда определяется при поступлении с распределителя (n+1)-ro импульса.

Цифровой эквивалент u_х снимается в конце цикла преобразования. На рис. 5.13 показана последовательность определения двоичного цифрового эквивалента при поразрядном уравновешивании напряжения u_х = 26 В.

Компенсирующие напряжения разрядов, вошедших в состав u_х, изображены сплошными линиями и отмечены внизу знаком 1. Компенсирующие напряжения разрядов, не вошедших в состав u_х, изображены пунктиром и отмечены внизу знаком 0. В результате уравновешивания получен двоичный эквивалент числа 26—011010.

Аналого-цифровые преобразователи считывания. АЦП считывания называют также преобразователями параллельного сравнения. В этих преобразователях для каждого уровня квантования предусматривается свое опорное напряжение u_{ο i} и свой орган сравнения ОС _i (рис. 5.14). Опорные напряжения снимаются с последовательного резисторного делителя. Входное напряжение u_х одновременно подается на все схемы сравнения. Часть схем, для которых выполняется условие u_x>u_{o i}, срабатывает, и мы получаем цифровой эквивалент u_х в унитарном коде (с основанием m=1). Преобразование этого кода в двоичный осуществляется специальной логической схемой, которую называют дешифратором или кодирующей логикой.

Такая простая структура дает возможность обеспечить чрезвычайно высокое быстродействие. Преобразование выполняется за один цикл, длительность которого при современной технологии изготовления интегральных схем может быть сделана менее 50 нc. Таким образом, АЦП считывания являются самыми быстродействующими из известных.