 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Глава 3. Количественная оценка информации 2 страница
|
|

или
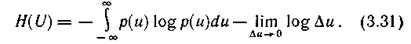
Эта величина при Δu→0 стремится к бесконечности, что полностью соответствует интуитивному представлению о том, что неопределенность выбора из бесконечно большого числа возможных состояний (значений) бесконечно велика.
Первый член в правой части соотношения (3.31) имеет конечное значение, которое зависит только от закона распределения непрерывной случайной величины U и не зависит от шага квантования Δu. Он имеет точно такую же структуру, как энтропия дискретного источника.
Второй член того же соотношения, наоборот, зависит лишь от шага квантования случайной величины U. Именно в нем кроется причина того, что величина H(U) обращается в бесконечность.
К использованию и трактовке соотношения (3.31) для получения конечной характеристики информационных свойств непрерывного источника известны два подхода.
Один подход состоит в том, что в качестве меры неопределенности непрерывного источника принимают первый член соотношения (3.31):

Поскольку для определения этой величины используется только функция плотности вероятности, т. е. дифференциальный закон распределения, она получила название относительной дифференциальной энтропии или просто дифференциальной энтропии непрерывного источника информации (непрерывного распределения случайной величины U).
Ее можно трактовать как среднюю неопределенность выбора случайной величины U с произвольным законом распределения по сравнению со средней неопределенностью выбора случайной величины U', изменяющейся в диапазоне, равном единице, и имеющей равномерное распределение.
Действительно, запишем соотношение (3.31) для случайной величины U', равномерно распределенной в интервале δ:

При δ=1

откуда при Δu=Δu'

Аналогично, используя операции квантования и предельного перехода, найдем выражение для условной энтропии непрерывного источника информации:
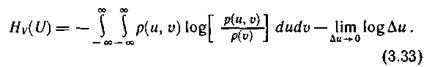
Отметим, что второй член в первой части выражения (3.33) идентичен соответствующему члену в соотношении (3.31). Обозначим первый член правой части выражения (3.33) через h 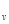 (U):
(U):

Эта величина конечна и называется относительной дифференциальной условной энтропией или просто дифференциальной условной энтропией непрерывного источника. Она характеризует неопределенность выбора непрерывной случайной величины U при условии, что известны результаты реализации значений другой статистически связанной с ней непрерывной случайной величины V, и по сравнению со средней неопределенностью выбора случайной величины U', изменяющейся в диапазоне, равном единице, и имеющей равномерное распределение вероятностей.
При втором подходе к использованию соотношения (3.31) для количественного определения информационных свойств непрерывного источника информации предлагается принять во внимание практическую невозможность обеспечения бесконечно высокой точности различения определенных значений непрерывной величины U. Поэтому все бесконечное число значений U в пределах заданной точности измерений следует рассматривать как одно значение.
Из средней неопределенности выбора источником u некоторого значения в этом случае необходимо вычесть среднюю неопределенность того же источника, полученную при условии, что мы знаем результаты определения U с некоторой определенной точностью ε. Тогда информационные свойства непрерывного источника будут оцениваться разностью безусловной и условной энтропий, определяемых соотношениями (3.31) и (3.33) соответственно. Такая разность, как будет показано в § 3.5, является мерой снятой неопределенности, называемой количеством информации.
Таким образом, при втором подходе безусловная и условная энтропии непрерывного источника рассматриваются лишь как некоторые вспомогательные величины, с помощью которых можно определить количество информации. Соотношение между понятиями энтропии и количества информации для непрерывного источника информации подобно соотношению между потенциалом, определенным с привлечением понятия бесконечности, и напряжением, определенным как разность потенциалов.
Поскольку вторые члены в правых частях соотношений (3.31) и (3.33) одинаковы, разность безусловной и условной энтропий непрерывного источника информации равна разности дифференциальных безусловной и условной энтропий того же источника, причем относительность их уже несущественна, так как разность не зависит от стандарта, с которым они сравнивались.
§ 3.5. СВОЙСТВА ДИФФЕРЕНЦИАЛЬНОЙ ЭНТРОПИИ
1. Дифференциальная энтропия в отличие от энтропии дискретного источника является относительной мерой неопределенности. Ее значение зависит от масштаба случайной величины U, а следовательно, и от выбора единицы ее измерения.
Изменим масштаб случайной величины U, например, в k раз, оставив неизменным масштаб равномерно распределенной в единичном интервале случайной величины U', принятой за эталон. Если  то
то  .
.
Тогда

Если одновременно изменить масштаб величины U', то относительная неопределенность также изменится, так как значение эталона будет уже иным.
Из относительности дифференциальной энтропии следует, что энтропия может принимать положительные, отрицательные и нулевые значения.
2. Дифференциальная энтропия не зависит от конкретных значений случайной величины U и, в частности, от изменения всех ее значений на постоянное. Действительно, масштаб U при этом не меняется и справедливо равенство
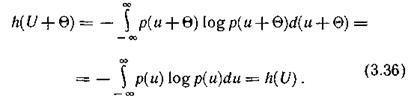
3. Какие же непрерывные распределения обладают максимальной дифференциальной энтропией?
а. Если единственным ограничением для случайной величины U является область ее возможных значений [α, β], то максимальной дифференциальной энтропией обладает равномерное распределение вероятностей в этой области.
При доказательстве решается задача определения плотности распределения р(u), обеспечивающей максимальное значение функционала

при ограничении

Используя, например, метод неопределенных множителей Лагранжа, получим

Нетрудно убедиться в том, что найденная функция р(u) обеспечивает максимум функционала h(U), причем

б. Если ограничения на область значений непрерывной случайной величины U отсутствуют, но известно, что дисперсия ее ограничена, то максимальной дифференциальной энтропией обладает нормальное распределение величины U.
При доказательстве решается задача определения функции р(u), обеспечивающей максимальное значение функционала

при ограничениях

где σ — среднеквадратическое отклонение от математического ожидания Ū =0 (σ — заданное ограничение).
Искомую плотность распределения р(u) находят, например, методом неопределенных множителей Лагранжа.
Она оказывается гауссовской:
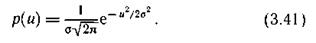
Вычислив функционал (3.40) для этого распределения, получим значение максимальной дифференциальной энтропии  . В двоичных единицах неопределенности
. В двоичных единицах неопределенности

Поскольку в информационных системах сигнал, описываемый случайной величиной U, часто представляет собой электрическое напряжение (или ток), дисперсия U пропорциональна средней мощности сигнала. Тогда в соответствии с (3.41) можно утверждать, что при заданной мощности наибольшей средней неопределенностью выбора будет обладать источник, генерирующий сигналы, амплитуды которых распределены по нормальному закону.
4. Соотношения для дифференциальной энтропии объединения статистически зависимых непрерывных источников аналогичны соответствующим формулам для дискретных источников:

где

Справедливость соотношения (3.43) легко проверить подстановкой выражения (3.32), заданного для h(V), и выражения (3.34) —для  .
.
Так как

то

причем равенство имеет место только в случае отсутствия статистической связи между U и V.
Пример 3.6. Определить, насколько мы выиграем в мощности, используя для организации мешающего воздействия, характеризующегося энтропией, источник шума с гауссовской плотностью распределения по сравнению с источником, имеющим в интервале [α, β] равномерную плотность распределения.
В соответствии с (3.42) дифференциальная энтропия гауссовского распределения
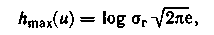
где σ  — дисперсия, характеризующая мощность, выделяемую на резисторе с сопротивлением в 1 Ом.
— дисперсия, характеризующая мощность, выделяемую на резисторе с сопротивлением в 1 Ом.
Для равномерного распределения энтропия определена соотношением (3.39):

Вычислим дисперсию σ  равномерного на интервале [α, β] распределения:
равномерного на интервале [α, β] распределения:

Из условия обеспечения равенства энтропий следует

Возведя (3.46) в квадрат и подставив в (3.44), получим

Следовательно, искомый выигрыш составляет 42 %.
§ 3.6. КОЛИЧЕСТВО ИНФОРМАЦИИ КАК МЕРА СНЯТОЙ НЕОПРЕДЕЛЕННОСТИ
Передача информации инициируется либо самим источником информации, либо осуществляется по запросу. Она диктуется желанием устранить неопределенность относительно последовательности состояний, реализуемых некоторым источником информации. Обычно запрос обусловлен отсутствием возможности наблюдать состояния источника непосредственно. Поэтому абонент обращается к информационной системе, которая извлекает интересующую его информацию из источника посредством некоторого первичного преобразователя и направляет ее по каналу связи абоненту.
Информация проявляется всегда в форме сигналов. Сигналы z, поступающие с выхода первичного преобразователя источника информации на вход канала связи, принято называть сообщениями в отличие от сигнала u, формирующихся на входе линии связи. В зависимости от формы создаваемых сообщений различают источники дискретных и непрерывных сообщений.
Отдельные первичные сигналы с выхода источника дискретных сообщений называют элементами сообщения. Каждому элементу сообщения соответствует определенное состояние источника информации. В случае параллельной реализации источником информации множества состояний, как это имеет место, например, в документах с печатным текстом, первичный преобразователь, в частности, обеспечивает их последовательное отображение элементами сообщения. Таким преобразователем может быть как автоматическое читающее устройство, так и человек.
Основное понятие теории информации — количество информации — рассматривается в данном параграфе применительно к передаче отдельных статистически несвязанных элементов сообщения. Дискретный источник сообщений при этом полностью характеризуется ансамблем

а непрерывный — одномерной плотностью распределения случайной величины — z — ρ(z). Особенности определения количества информации при передаче сообщений изложены в § 4.2.
Передача информации от дискретного источника. Выясним, насколько будет изменяться неопределенность относительно состояния источника сообщения при получении адресатом элемента сообщения с выхода канала связи. Алфавиты передаваемых и принимаемых элементов сообщения считаем идентичными.
Вследствие воздействия помех полученный элемент сообщения в общем случае отличается от переданного. Подчеркнем это различие. Обозначив принимаемые элементы сообщения другими буквами: 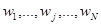 .
.
Априорная неопределенность (неопределенность до получения элемента сообщения) относительно состояния источника не является полной. Предполагается, что адресату известен алфавит элементов сообщения, а из прошлого опыта он знает вероятности их появления. Считая, что состояния источника реализуются независимо, априорная частная неопределенность появления элемента сообщения 

где  — априорная вероятность появления элемента сообщения
— априорная вероятность появления элемента сообщения  .
.
Предполагаются также известными некоторые сведения относительно помехи в канале связи. Обычно считают, что между элементами сообщения и помехой статистические связи отсутствуют, искажения отдельных элементов сообщения являются событиями независимыми и адресату известна совокупность условных вероятностей 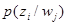
 того, что вместо элемента сообщения
того, что вместо элемента сообщения  , будет принят элемент сообщения
, будет принят элемент сообщения  .
.
При получении конкретного элемента сообщения  , адресату становится известным значение условной вероятности
, адресату становится известным значение условной вероятности 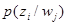 , называемой апостериорной (послеопытной) вероятностью реализации источником элемента сообщения
, называемой апостериорной (послеопытной) вероятностью реализации источником элемента сообщения  . Это позволяет найти апостериорную частную неопределенность, остающуюся у адресата относительно выдачи источников элемента сообщения
. Это позволяет найти апостериорную частную неопределенность, остающуюся у адресата относительно выдачи источников элемента сообщения  после получения конкретного элемента сообщения
после получения конкретного элемента сообщения  :
:

Поскольку получение информации мы связываем с уменьшением неопределенности, естественно определить частное количество информации  , получаемое при приеме элемента сообщения
, получаемое при приеме элемента сообщения  относительно некоторого реализованного источником элемента сообщения
относительно некоторого реализованного источником элемента сообщения  как разность частных неопределенностей, имевшихся у адресата до и после получения элемента сообщения (априорной и апостериорной):
как разность частных неопределенностей, имевшихся у адресата до и после получения элемента сообщения (априорной и апостериорной):

Анализ формулы (3.47) позволяет сделать следующие заключения:
1) частное количество информации растет с уменьшением априорной и увеличением апостериорной вероятностей реализации элемента сообщения источником, что находится в полном соответствии с нашими интуитивными представлениями;
2) частное количество информации об элементе сообщения  может быть не только положительным, но и отрицательным, а также нулем, что зависит от соотношения априорной
может быть не только положительным, но и отрицательным, а также нулем, что зависит от соотношения априорной  и апостериорной
и апостериорной 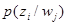 вероятностей. Если вероятность того, что источником был реализован элемент сообщения
вероятностей. Если вероятность того, что источником был реализован элемент сообщения  увеличилась после приема элемента сообщения
увеличилась после приема элемента сообщения  , т. е.
, т. е. 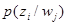 >
>  , то полученное частное количество информации положительно. Если эта вероятность не изменилась, т. е.
, то полученное частное количество информации положительно. Если эта вероятность не изменилась, т. е. 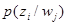 =
=  , то имевшая место неопределенность тоже не изменилась и частное количество информации равно нулю.
, то имевшая место неопределенность тоже не изменилась и частное количество информации равно нулю.
Наконец, случай 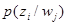 <
<  соответствует увеличению неопределенности относительно реализации
соответствует увеличению неопределенности относительно реализации  после получения элемента сообщения
после получения элемента сообщения  , и, следовательно, частное количество информации отрицательно;
, и, следовательно, частное количество информации отрицательно;
3) в случае отсутствия помехи апостериорная вероятность 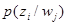 = 1. При этом частное количество информации численно совпадает с частной априорной неопределенностью реализации данного элемента сообщения
= 1. При этом частное количество информации численно совпадает с частной априорной неопределенностью реализации данного элемента сообщения  :
:

Это максимальное частное количество информации, которое можно получить об элементе сообщения  ;
;
4) частное количество информации относительно реализации источником элемента сообщения  , содержащееся в принятом элементе сообщения
, содержащееся в принятом элементе сообщения  , равно частному количеству информации относительно
, равно частному количеству информации относительно  , содержащемуся в элементе сообщения
, содержащемуся в элементе сообщения  :
:

Хотя имеют место случаи, где важно оценить частное количество информации  , для задач анализа и оптимизации функционирования информационных систем более рациональны усредненные характеристики, отражающие статистические свойства источника информации и канала связи.
, для задач анализа и оптимизации функционирования информационных систем более рациональны усредненные характеристики, отражающие статистические свойства источника информации и канала связи.
Найдем среднее количество информации, содержащееся в любом принятом элементе сообщения относительно переданного (реализованного) источником. До получения конкретного элемента сообщения средняя неопределенность, имеющаяся у адресата, относительно реализации источником любого элемента сообщения равна энтропии источника. Ее называют априорной энтропией источника.
Средняя неопределенность относительно любого состояния источника, остающаяся у адресата после получения конкретного элемента сообщения  , характеризуется частной условной энтропией
, характеризуется частной условной энтропией  :
:

Это случайная величина, зависящая от того, какой конкретно элемент сообщения принят.
Средняя неопределенность по всему ансамблю принимаемых элементов сообщений равна условной энтропии источника  :
:

или
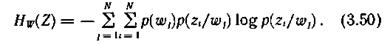
Эту условную энтропию называют апостериорной энтропией источника информации.
Таким образом, при наличии помех среднее количество информации, содержащееся в каждом принятом элементе сообщения, относительно любого переданного равно разности априорной и апостериорной энтропии источника:

Представив априорную и апостериорную энтропии соответственно выражениями (3.6) и (3.50) и проведя несложные преобразования, получим формулу для количества информации непосредственно через вероятности:

Если частный характер количества информации специально не оговаривается, мы всегда имеем дело с количеством информации, приходящимся в среднем на один элемент сообщения. Поэтому указание об усреднении опускается.
Передача информации от непрерывного источника. Количество информации, получаемой от непрерывного источника по каналу с помехами, определяется так же, как в случае, рассмотренном выше, но с использованием понятия дифференциальной энтропии.
Для источника, имеющего непрерывное множество состояний, среднее количество информации, содержащееся в каждом принятом значении случайной величины  относительно переданного значения случайной величины Ζ, можно получить как разность априорной и апостериорной дифференциальных энтропий:
относительно переданного значения случайной величины Ζ, можно получить как разность априорной и апостериорной дифференциальных энтропий:

Соотношение (3.53) несложно выразить в виде, подобном (3.52):

Относительность дифференциальных энтропий в этом случае не принимается во внимание, поскольку количество информации не зависит от выбранного стандарта сравнения.
Основные свойства количества информации. 1. Несмотря на то, что частное количество информации может быть величиной отрицательной, количество информации неотрицательно.
Действительно, согласно выражению

Тогда

2. При отсутствии статистической связи между случайными величинами Ζ и W

следовательно, в этом случае

(принятые элементы сообщения не несут никакой информации относительно переданных).
3. Количество информации в W относительно Ζ равно количеству информации в Ζ относительно W.
Для доказательства этого утверждения воспользуемся выражением

Аналогично можно записать

Так как

то

откуда

4. При взаимно однозначном соответствии между множествами передаваемых и принимаемых элементов сообщений, что имеет место в отсутствии помехи, апостериорная энтропия равна нулю и количество информации численно совпадает с энтропией источника:

Это максимальное количество информации о состоянии дискретного источника. Для непрерывного источника оно равно бесконечности.
Пример 3.7. Выстрел из орудия не поражает цель с вероятностью р. Через какое число выстрелов следует поинтересоваться у разведчика-корректировщика, уничтожена ли цель, чтобы в результате ответа получить максимальное количество информации?
Ансамбль интересующих нас событий включает: 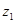 — цель поражена;
— цель поражена; 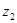 — цель не поражена. Вероятность того, что цель не поражена после k выстрелов, равна
— цель не поражена. Вероятность того, что цель не поражена после k выстрелов, равна  . Вероятность противоположного события (1—
. Вероятность противоположного события (1—  ). Поскольку после ответа корректировщика неопределенность устраняется полностью, количество информации равно энтропии, а она максимальна при равновероятности событий. Следовательно,
). Поскольку после ответа корректировщика неопределенность устраняется полностью, количество информации равно энтропии, а она максимальна при равновероятности событий. Следовательно,

откуда

Пример 3.8. Определить среднее количество информации, получаемое при передаче элемента сообщения по каналу, описанному матрицей совместных вероятностей передачи и приема элементов сообщения

Безусловные вероятности посылаемых z и принимаемых w элементов сообщения определены при рассмотрении примера 3 4. Там же получены значения для априорной H(Z) и апостериорной  энтропий.
энтропий.
В соответствии с (3.51)

§ 3.7. ЭПСИЛОН-ЭНТРОПИЯ СЛУЧАЙНОЙ ВЕЛИЧИНЫ
Ранее было показано, что неопределенность реализации непрерывным источником информации состояния в конкретный момент времени (отсчета) равна бесконечности. Тем более равна бесконечности неопределенность реализации непрерывным источником конкретного сигнала длительности Т.
Однако такой результат получен в предположении возможности фиксировать любые сколь угодно малые различия между реализациями. На практике такая возможность отсутствует. Это объясняется тем, что воспринимающие информацию датчики, включая человека, обладают ограниченной чувствительностью и конечной разрешающей способностью, а также тем, что процесс восприятия сопровождается помехами.
Если учесть, что нас интересует приближенное восприятие реализации, то количество информации, приходящееся на отсчет или на единицу времени, можно вычислить.
Дата публикования: 2015-11-01; Прочитано: 1504 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
