 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Глава 3. Количественная оценка информации 3 страница
|
|
Ограничимся рассмотрением простейшего случая, когда отдельные состояния источника информации представляют собой независимые реализации случайной величины U. (Эпсилон - энтропия случайного процесса рассмотрена в § 4.4.)
Ансамбль реализаций случайной величины U описывается плотностью распределения вероятностей р(u). О значениях случайной величины U можно судить по значениям другой случайной величины Ζ, если мера их различия не превышает заданной верности воспроизведения. В этом случае говорят, что Ζ воспроизводит U.
Для количественной оценки степени сходства сигналов целесообразно ввести какую-либо функцию ρ(z, u), имеющую природу «расстояния». Тогда удобным критерием верности V(Z, U) является среднее значение функции p(z, u), взятое по всему множеству значений z и u:
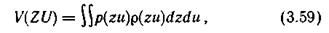
где ρ(z, u) — плотность совместного распределения вероятностей величин Ζ и U.
Наиболее широко используется среднеквадратический критерий, при котором ρ(z, u) представляет собой квадрат обычного евклидова расстояния между точками в соответствующем пространстве (см. § 2.12).
Требование к верности в данном случае задается с использованием критерия V(ZU):
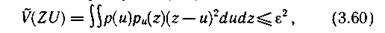
где 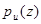 — условная плотность распределения — функция правдоподобия того, что конкретный сигнал u будет воспроизведен как сигнал z; ε — заданное значение верности.
— условная плотность распределения — функция правдоподобия того, что конкретный сигнал u будет воспроизведен как сигнал z; ε — заданное значение верности.
Так как плотность р(u) определена, то для выполнения условия (3.60) варьировать можно только условной плотностью распределения 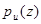 .
.
Если случайная величина Ζ воспроизводит случайную величину U с некоторой верностью ε, то количество информации, содержащееся в воспроизводящей величине Ζ относительно U, конечно и в соответствии с (3.54) может быть записано в форме
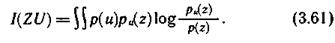
где

- плотность воспроизводящей величины Ζ.
Желательно обеспечить заданную верность воспроизведения при минимальном количестве получаемой информации. Поэтому среди множества функций 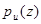 , удовлетворяющих условию (3.60), целесообразно выбрать такую, которая обеспечивает наименьшее I(ZU) [10, 35].
, удовлетворяющих условию (3.60), целесообразно выбрать такую, которая обеспечивает наименьшее I(ZU) [10, 35].
Минимальное количество информации в одной случайной величине Ζ относительно другой U, при котором удовлетворяется заданное требование к верности воспроизведения величины U, называется ε-энтропией величины U и обозначается  :
:

при

Используя безусловную 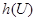 и условную
и условную  дифференциальные энтропии величины U, выражение (3.63) можно представить в виде
дифференциальные энтропии величины U, выражение (3.63) можно представить в виде
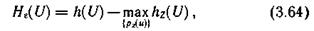
где 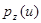 — условная плотность вероятности того, что в тех случаях, когда был принят сигнал z, передавался сигнал u.
— условная плотность вероятности того, что в тех случаях, когда был принят сигнал z, передавался сигнал u.
Пример 3.9. Найти  источника информации, ансамбль состояний которого описывается нормально распределенной случайной величиной U с дисперсией
источника информации, ансамбль состояний которого описывается нормально распределенной случайной величиной U с дисперсией 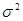 при верности воспроизведения
при верности воспроизведения 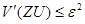 .
.
Будем считать, что заданная верность воспроизведения обусловлена действием аддитивной статистически не связанной с сигналом помехой Ξ, причем Μ [Ξ] =0 и Μ[Ξ 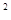 ] = ε
] = ε 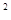 . Передаваемый сигнал u рассматриваем как сумму воспроизводящего сигнала z и помехи u=z+
. Передаваемый сигнал u рассматриваем как сумму воспроизводящего сигнала z и помехи u=z+ 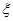 .
.
Так как в данном случае  в выражении (3.64) полностью определяется помехой
в выражении (3.64) полностью определяется помехой
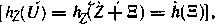
то
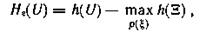
где h(Ξ) — дифференциальная энтропия помехи; ρ(ξ) — плотность распределения помехи Ξ.
Ранее [см. (3.41)] нами установлено, что при ограничении на дисперсию случайной величины максимальной дифференциальной энтропией обладает нормальное распределение. Поэтому в соответствии с (3.42) получаем
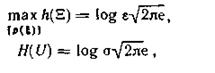
откуда
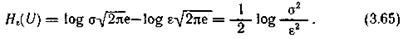
Так как σ 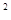 определяет среднюю мощность Р
определяет среднюю мощность Р  сигнала, а ε
сигнала, а ε 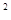 — среднюю мощность ρ
— среднюю мощность ρ 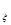 помехи Ξ, то выражение (3.65) характеризует зависимость эпсилон - энтропии от величины
помехи Ξ, то выражение (3.65) характеризует зависимость эпсилон - энтропии от величины  , называемой отношением сигнал/помеха.
, называемой отношением сигнал/помеха.
При заданном отношении сигнал/помеха значение H 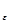 (U) для нормально распределенной случайной величины является максимально возможным.
(U) для нормально распределенной случайной величины является максимально возможным.
Для произвольно распределенной случайной величины U при том же критерии верности и малых ε [когда H 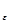 (U) велико] справедливо приближенное равенство
(U) велико] справедливо приближенное равенство
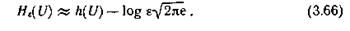
Контрольные вопросы
1. В чем сущность требования аддитивности к мере неопределенности выбора?
2. Назовите основной недостаток меры неопределенности, предложенной Хартли.
3. В каких единицах измеряется неопределенность выбора?
4. Какие требования предъявляются к мере неопределенности выбора из дискретного ансамбля?
5. Охарактеризуйте сущность понятия энтропии.
6. Изложите основные свойства энтропии дискретного ансамбля.
7. Запишите выражение для условной энтропии и поясните ее смысл.
8. Как определить энтропию нескольких взаимозависимых ансамблей?
9. Какова особенность определения энтропии непрерывного источника информации?
10. Дайте определение дифференциальной энтропии и сформулируйте ее основные свойства.
11. Какие распределения обладают максимальной дифференциальной энтропией:
а) при ограничении на диапазон изменения случайной величины?
б) при ограничении на дисперсию случайной величины?
12. Как связаны между собой понятия количества информации и энтропии?
13. Чем различаются понятия частного и среднего количества информации?
14. Сформулируйте основные свойства количества информации.
15. Запишите выражения для определения количества информации при неполной достоверности передачи:
а) от дискретного источника;
б) от непрерывного источника.
16. В чем сущность эпсилон - энтропии случайной величины?
17. Охарактеризуйте среднеквадратический критерий верности воспроизведения.
18. Покажите, что при среднеквадратическом критерии верности воспроизведения эпсилон - энтропия максимальна для нормально распределенной случайной величины с ограниченной дисперсией.
ГЛАВА 4. ИНФОРМАЦИОННЫЕ ХАРАКТЕРИСТИКИ ИСТОЧНИКА СООБЩЕНИЙ И КАНАЛА СВЯЗИ
§ 4.1. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ
Опираясь на формализованное описание сигналов и введенную меру количества информации, рассмотрим информационные характеристики источников сообщений и каналов связи, позволяющие установить пути повышения эффективности систем передачи информации, и, в частности, определить условия, при которых можно достигнуть максимальной скорости передачи сообщений по каналу связи как в отсутствие, так и при наличии помех.
Источники сообщений и каналы связи в системах передачи отличаются большим разнообразием по своей структуре и физической природе. Используются механические, акустические, оптические, электрические и радиоканалы. Для выяснения общих закономерностей необходимо абстрагироваться от их конкретного физического воплощения и оперировать формализованными понятиями источника сообщения и канала связи.
Источник дискретных сообщений формирует дискретные последовательности из ограниченного числа элементарных сообщений. На выходе источника непрерывных сообщений образуются непрерывные сообщения. Источник сообщений в теории информации полностью определяется статистическими данными о формируемых им сообщениях.
Под каналом связи подразумевают совокупность устройств и физических сред, обеспечивающих передачу сообщений из одного места в другое (или от одного момента времени до другого). Если канал используется для передачи дискретных сообщений, он называется дискретным каналом. Непрерывным будем называть канал, предназначенный для передачи непрерывных сообщений.
Так как в процессе передачи дискретных сообщений модулятором в соответствии с поступающей последовательностью символов осуществляется изменение информативного параметра непрерывного (чаще всего высокочастотного) сигнала, генерируемого передатчиком в линию связи, то часть дискретного канала от выхода модулятора до входа демодулятора (рис. 4.1) является непрерывным каналом связи. Включив в состав этого канала на передающей стороне модулятор, а на приемной — демодулятор, получим дискретный канал, характеризуемый на входе множеством символов u, а на выходе — множеством символов υ.
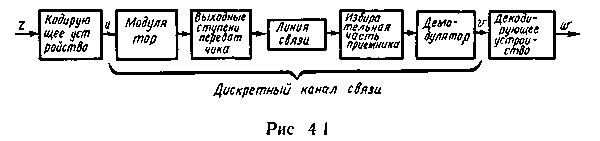
Для достижения определенных целей в указанный дискретный канал могут быть введены кодирующие и декодирующие устройства. При этом получаем дискретный канал связи, на вход которого поступают сообщения z, а выходом являются сообщения w, направляемые адресату. Отметим, что непрерывные сообщения z(t) путем дискретизации и квантования всегда можно преобразовать в дискретные и, таким образом, перейти от непрерывного канала к дискретному.
Если вредным действием помех в канале можно пренебречь, то для анализа используется модель в виде идеализированного канала, называемого каналом без помех. В идеальном канале каждому сообщению на входе однозначно соответствует определенное сообщение на выходе и наоборот.
Когда требования к достоверности велики и пренебрежение неоднозначностью связи между сообщениями z и w недопустимо, используется более сложная модель — канал с помехами.
Канал считается заданным, если известны статистические данные о сообщениях на его входе и выходе и ограничения, накладываемые на входные сообщения физическими характеристиками канала. Канал прямой передачи (от источника сообщений к их получателю), дополненный обратным каналом, например, для запроса повторной передачи в случае обнаружения ошибки, называют каналом с обратной связью.
§ 4.2. ИНФОРМАЦИОННЫЕ ХАРАКТЕРИСТИКИ ИСТОЧНИКА ДИСКРЕТНЫХ СООБЩЕНИЙ
Модели источника дискретных сообщений. В гл. 3 речь шла о средней неопределенности и среднем количестве информации, приходящимся на одно состояние источника сообщений. Математической моделью множества возможных реализаций источника была дискретная или непрерывная случайная величина.
На практике, однако, нас чаще всего интересует не одно конкретное состояние источника, а дискретные или непрерывные последовательности состояний, реализуемых источником за длительный промежуток времени, например телеграммы, видеосюжеты и т. п. Для описания таких сообщений используются математические модели в виде дискретных и непрерывных случайных процессов.
Для построения модели необходимо знать объем l алфавита знаков (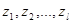 ), из которых источником формируются сообщения, и вероятности создания им отдельных знаков с учетом возможной взаимосвязи между ними.
), из которых источником формируются сообщения, и вероятности создания им отдельных знаков с учетом возможной взаимосвязи между ними.
При доказательстве основных положений теории информации Шенноном использовалась модель, называемая эргодическим источником сообщений. Предполагается, что создаваемые им сообщения математически можно представить в виде эргодической случайной последовательности. Такая последовательность, как известно, удовлетворяет условиям стационарности и эргодичности. Первое означает, что вероятности отдельных знаков и их сочетаний не зависят от расположения последних по длине сообщения. Из второго следует, что статистические закономерности, полученные при исследовании одного достаточно длинного сообщения с вероятностью, близкой к единице, справедливы для всех сообщений, создаваемых источником. Из статистических характеристик в данном случае нас интересует средняя неопределенность в расчете на один знак последовательности.
Стационарный источник сообщений, выбирающий каждый знак формируемой последовательности независимо от других знаков, всегда является эргодическим. Его также называют источником без памяти.
На практике, однако, чаще встречаются источники, у которых вероятность выбора одного знака сообщения зависит от того, какие знаки были выбраны источником до этого (источники с памятью). Поскольку такая связь, как правило, распространяется на ограниченное число предыдущих знаков, для описания функциони-рования источника целесообразно использовать цепи Маркова.
Цепь Маркова порядка n характеризует последовательность событий, вероятности которых зависят от того, какие n событий предшествовали данному. Эти n конкретных событий определяют состояние источника, в котором он находится при выдаче очередного знака. При объеме алфавита знаков l число R различных состояний источника не превышает 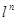 . Обозначим эти состояния через
. Обозначим эти состояния через  , а вероятности выбора в состоянии
, а вероятности выбора в состоянии  знака
знака  — через
— через 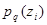 . При определении вероятности
. При определении вероятности 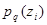 естественно предположить, что к моменту выдачи источником очередного знака известны все знаки, созданные им ранее, а следовательно, и то, в каком состоянии находится источник.
естественно предположить, что к моменту выдачи источником очередного знака известны все знаки, созданные им ранее, а следовательно, и то, в каком состоянии находится источник.
Если источник находится в состоянии  , его частная энтропия H(
, его частная энтропия H( ) определяется соотношением
) определяется соотношением
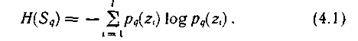
Усредняя случайную величину H( ) по всем возможным состояниям q =
) по всем возможным состояниям q =  , получаем энтропию источника сообщений:
, получаем энтропию источника сообщений:

где p( ) — вероятность того, что источник сообщений находится в состоянии
) — вероятность того, что источник сообщений находится в состоянии  .
.
Величина H(Z) характеризует неопределенность, приходящуюся в среднем на один знак, выдаваемый источником сообщений.
Определим энтропию источника сообщений для нескольких частных случаев.
Если статистические связи между знаками полностью отсутствуют, то после выбора источником знака  , его состояние не меняется (R = 1). Следовательно, p(
, его состояние не меняется (R = 1). Следовательно, p(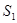 )= 1, и для энтропии источника сообщений справедливо выражение:
)= 1, и для энтропии источника сообщений справедливо выражение:
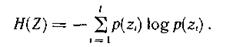
Когда корреляционные связи наблюдаются только между двумя знаками (простая цепь Маркова), максимальное число различных состояний источника равно объему алфавита. Следовательно, R= l и 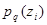 =
=  , где q =
, где q = 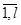 . При этом выражение (4.2) принимает вид
. При этом выражение (4.2) принимает вид

При наличии корреляционной связи между тремя знаками состояния источника определяются двумя предшествующими знаками. Поэтому для произвольного состояния источника  , удобно дать обозначение с двумя индексами
, удобно дать обозначение с двумя индексами 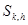 , где k=
, где k= 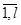 и h=
и h= 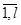 .
.
Тогда

Подставляя эти значения в (4.2), находим
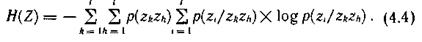
Аналогично можно получить выражения для энтропии источника сообщений и при более протяженной корреляционной связи между знаками.
Пример 4.1. Определить, является ли эргодическим стационарный дискретный источник сообщений, алфавит которого состоит из четырех знаков 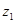
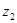
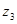 и
и 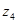 , причем безусловные вероятности выбора знаков одинаковы [
, причем безусловные вероятности выбора знаков одинаковы [ 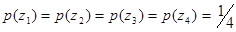 ], a условные вероятности
], a условные вероятности  заданы табл 4.1.
заданы табл 4.1.
Таблица 4.1.
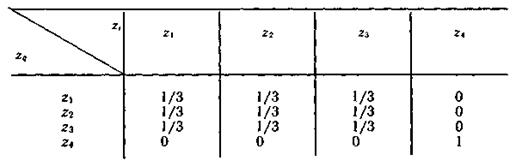
Анализ табл. 4.1 показывает, что источник имеет два режима работы. С вероятностью, равной ¾, первым будет выбран один из знаков 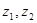 или
или 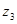 и источник начнет формировать последовательность с равновероятным появлением знаков. Если же первым будет выбран знак
и источник начнет формировать последовательность с равновероятным появлением знаков. Если же первым будет выбран знак 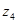 (вероятность такого случая равна
(вероятность такого случая равна  ), то генерируется последовательность, содержащая только знаки
), то генерируется последовательность, содержащая только знаки 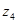 .
.
Усреднение по ансамблю предполагает наличие множества однотипных источников, примерно три четверти из которых будет работать в первом режиме, а остальные — во втором. При этом в соответствии с (4.3) энтропия источника
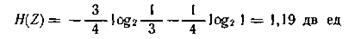
Среднее по последовательности (времени) вычисляется с использованием конкретной последовательности и поэтому зависит от режима функционирования источника. В первом режиме неопределенность, приходящаяся на один знак достаточно длинной последовательности (энтропия последовательности), равна 1,586 дв. ед., а во втором — нулю.
Поскольку энтропии формируемых последовательностей не совпадают с энтропией источника, он не является эргодическим.
Отметим, однако, что любой стационарный источник сообщений может быть представлен совокупностью нескольких эргодических источников, различающихся режимами работы [22].
Свойства эргодических последовательностей знаков. Характер последовательностей, формируемых реальным источником сообщений, зависит от существующих ограничений на выбор знаков. Они выражаются в том, что вероятности реализации знаков различны и между ними существуют корреляционные связи. Эти ограничения приводят к тому, что вероятности формируемых последовательностей существенно различаются.
Пусть, например, эргодический источник без памяти последовательно выдает знаки 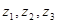 в соответствии с вероятностями 0,1; 0,3; 0,6. Тогда в образованной им достаточно длинной последовательности знаков мы ожидаем встретить в среднем на один знак
в соответствии с вероятностями 0,1; 0,3; 0,6. Тогда в образованной им достаточно длинной последовательности знаков мы ожидаем встретить в среднем на один знак 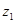 три знака
три знака 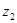 и шесть знаков
и шесть знаков 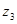 . Однако при ограниченном числе знаков в последовательности существуют вероятности того, что она будет содержать;
. Однако при ограниченном числе знаков в последовательности существуют вероятности того, что она будет содержать;
только знаки 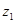 (либо
(либо 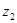 , либо
, либо 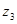 );
);
только знаки 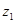 и один знак
и один знак 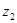 или
или 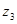 ;
;
только знаки 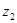 и один знак
и один знак 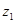 или
или 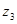 ;
;
только знаки 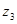 и один знак
и один знак 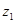 или
или 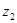 ;
;
только знаки 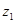 и два знака
и два знака 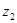 или
или 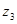 и т. д.
и т. д.
С увеличением числа знаков вероятности появления таких последовательностей уменьшаются.
Фундаментальные свойства длинных последовательностей знаков, создаваемых эргодическим источником сообщений, отражает следующая теорема: как бы ни малы были два числа δ>0 и μ>0 при достаточно большом Ν, все последовательности могут быть разбиты на две группы.
Одну группу составляет подавляющее большинство последовательностей, каждая из которых имеет настолько ничтожную вероятность, что даже суммарная вероятность всех таких последовательностей очень мала и при достаточно большом N будет меньше сколь угодно малого числа δ. Эти последовательности называют нетипичными.
Вторая группа включает типичные последовательности, которые при достаточно большом N отличаются тем, что вероятности их появления практически одинаковы, причем вероятность ρ любой такой последовательности удовлетворяет неравенству
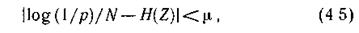
где Η(Ζ) — энтропия источника сообщений.
Соотношение (4.5) называют также свойством асимптотической равномерности длинных последовательностей. Рассмотрим его подробнее.
Поскольку при N→ ∞ источник сообщений с вероятностью, сколь угодно близкой к единице, выдает только типичные последовательности, принимаемое во внимание число последовательностей равно 1/р. Неопределенность создания каждой такой последовательности с учетом их равновероятности составляет log(l/p). Тогда величина log(l/p)/N представляет собой неопределенность, приходящуюся в среднем на один знак. Конечно, эта величина практически не должна отличаться от энтропии источника, что и констатируется соотношением (4.5).
Ограничимся доказательством теоремы для простейшего случая эргодического источника без памяти. Оно непосредственно вытекает из закона больших чисел, в соответствии с которым в длинной последовательности из N элементов алфавита l (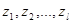 ), имеющих вероятности появления
), имеющих вероятности появления 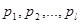 , содержится Np
, содержится Np  элементов
элементов 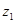 , Np
, Np  элементов
элементов 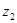 и т. д.
и т. д.
Тогда вероятность ρ реализации любой типичной последовательности близка к величине

Логарифмируя правую и левую части выражения (4.6), получаем
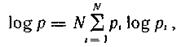
откуда (при очень больших Ν)

Для общего случая теорема доказывается с привлечением цепей Маркова.
Покажем теперь, что за исключением случая равновероятного и независимого выбора букв источником, когда нетипичные последовательности отсутствуют, типичные последовательности при достаточно большом N составляют незначительную долю от общего числа возможных последовательностей.
При объеме алфавита источника l и количестве знаков в последовательности N число всех возможных последовательностей
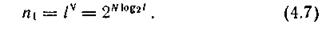
Принимая во внимание соотношение (4.5), число типичных последовательностей n  можно записать в виде
можно записать в виде

Тогда
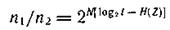
Так как
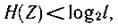
то
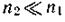
и неравенство усиливается с увеличением N.
К. Шеннон показал, что рассмотренные свойства длинных последовательностей могут служить основанием для осуществления эффективного кодирования информации (см. § 5.4).
Пример 4.2. Оценить, какую долю общего числа возможных последовательностей следует учитывать в практических расчетах, если эргодический источник характеризуется параметрами l = 16, Η(Ζ) = 3,5 дв.ед, а N = 50.
В соответствии с (4.7) и (4.8) имеем

откуда
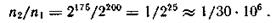
Дата публикования: 2015-11-01; Прочитано: 1342 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
