Глава 1 математические модели сигналов 5 страница

Идеализированный случайный процесс, энергетический спектр которого безграничен и равномерен, известен как «белый шум». Такое название возникло по аналогии с белым светом, имеющим равномерный и неограниченный спектр интенсивности. Основная особенность процесса в том, что его значения в любые два сколь угодно близкие моменты времени некоррелированы. Создать белый шум принципиально невозможно, так как реальные источники сигналов всегда имеют ограниченную мощность. Тем не менее, понятие «белый шум» нашло широкое применение в информационной технике. Такая модель может быть принята, например, для сигналов (шумов), имеющих равномерный энергетический спектр в пределах полосы пропускания входного блока системы, в которой они рассматриваются.

Иногда говорят о «реальном белом шуме», подразумевая стационарный случайный процесс с равномерным энергетическим спектром в пределах конечной, но достаточно широкой полосы частот.

Пример 1.8. Определить спектральную плотность мощности случайного процесса с линейно убывающей нормированной функцией автокорреляции (рис. 1.18).

Аналитическое выражение нормированной корреляционной функции запишем в виде

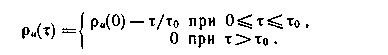
Воспользовавшись соотношением (1.105) при р„ (0) = 1, получим

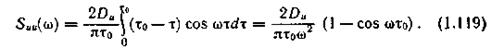
Раскрывая по правилу Лопиталя неопределенность выражения (1.119) при ω = 0, найдем

Несложный дополнительный анализ дает возможность определить форму кривой S_uu(w) (рис. 1.19).

Контрольные вопросы

1. В чем относительность сигнала и помехи?

2. Охарактеризуйте основной метод исследования сигналов.

3. Что понимают под детерминированным сигналом?

4. Назовите различные формы представления моделей сигналов.

5. В чем сущность спектрального представления сигналов?

6. Запишите условия ортогональности и ортонормированности системы функций.

7. Назовите преимущества частотного представления сигналов.

8. Дайте определение спектру амплитуд и спектру фаз.

9. В чем различие спектров периодического и непериодического сигналов?

10. Дайте определение практической ширины спектра периодического и непериодического сигналов.

11. Как связаны между собой длительность сигнала и ширина его спектра?

12. Каковы причины использования случайного процесса в качестве модели сигнала?

13. Назовите разновидности случайных функций времени.

14. В чем трудности точного математического описания случайного процесса?

15. Как определить математическое описание, дисперсию и корреляционную функцию случайного процесса?

16. Поясните физический смысл корреляционной функции, перечислите ее свойства.

17. Какой случайный процесс называется центрированным?

18. Дайте определение стационарности случайного процесса в узком и широком смысле.

19. Сформулируйте условие эргодичности стационарного случайного процесса.

20. Каков физический смысл дисперсии стационарного случайного процесса, имеющего размерность тока или напряжения

21. Что подразумевается под каноническим разложением случайного процесса?

22. Как определяются дисперсии случайных коэффициентов разложения по корреляционной функции процесса?

23. Запишите соотношения, связывающие корреляционную функцию стационарного случайного процесса с его спектральной плотностью.

24. Сформулируйте основные свойства спектральной плотности стационарного случайного процесса.

25. Какой случайный процесс называют белым шумом и каковы его основные характеристики?