Глава 1 математические модели сигналов 3 страница

Учитывая соотношения (1.15) и (1.16), запишем

Воспользовавшись формулой Эйлера (1.14) и обозначив φ(kw₁) через φ_k, окончательно получим

Распространена и другая тригонометрическая форма ряда Фурье, имеющая вид

Однако она менее удобна для практического применения. Отдельные составляющие в представлениях (1.23) и (1.24) называют гармониками. Как спектр амплитуд, так и спектр фаз периодического сигнала удобно представлять наглядно спектральными диаграммами. На диаграмме спектра амплитуд каждой гармонике ставится в соответствие вертикальный отрезок, длина которого пропорциональна амплитуде, а расположение на оси абсцисс отвечает частоте этой составляющей. Аналогично на диаграмме спектра фаз обозначают значения фаз гармоник. Поскольку в результате спектры отображаются совокупностями линий, их часто называют линейчатыми.

Отметим, что дискретный (линейчатый) спектр не обязательно должен принадлежать периодическому сигналу. Спектр периодического сигнала характеризует совокупность гармоник, кратных основной частоте ωι. Линейчатые спектры, включающие гармоники некратных частот, принадлежат так называемым почти периодическим сигналам. Диаграмма спектра амплитуд периодического сигнала показана на рис. 1.4. Огибающую A(t) этого спектра амплитуд можно получить, заменив kw₁ в A(kw₁) на ω, где ω = kω₁ для k-й гармоники.

Пример 1.1. Определить спектры амплитуд и фаз периодической последовательности прямоугольных импульсов длительностью τ и амплитудой u₀, следующих с частотой ω₁ = 2π/Τ (рис. 1.5).

Функция u(t), описывающая такую последовательность импульсов на периоде, может быть задана в виде:

В соответствии с (1.16) имеем

или

Амплитуды гармоник, включая постоянную составляющую, равную А₀/2, определим из выражения

при k = О, 1, 2,....

Выбор начала отсчета времени на их величину не влияет. Огибающая спектра амплитуд определяется видом функции

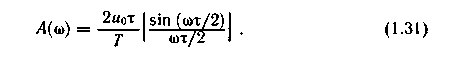
При ω = 0 получаем

Характер изменения амплитуд диктуется функцией sin х/х и не зависит от частоты следования импульсов. На частотах, кратных 2π/τ, огибающая спектра равна нулю.

На рис. 1.6 приведена диаграмма спектра амплитуд для случая

Τ/τ = 3[ω₁ = 2π/(3τ)]. Число составляющих в спектре бесконечно велико. Крутизна фронтов импульсов обусловлена наличием в спектре составляющих с частотами, существенно превышающими основную частоту ω₁.

Опираясь на формулу (1.29) и принимая во внимание, что знаки функции sin(kw₁ /2) на последовательности интервалов частот Δω = 2π/τ чередуются, выражение для спектра фаз запишем следующим образом:

где n — номер интервала частот ω = 2π/τ, отсчитываемого от ω = 0.

Спектр фаз зависит от выбора начала отсчета. Если передний фронт прямоугольного импульса последовательности приходится на начало отсчета времени, то на каждом интервале Δω = 2π/τ фазы составляющих возрастают линейно. Диаграмма спектра фаз последовательности прямоугольных импульсов для этого случая (Τ/τ = 3, t₁ = 0) показана на рис. 1.7.

Пример 1.2. Вычислить несколько первых членов ряда Фурье для периодической последовательности прямоугольных импульсов и проследить, как их гумма сходится к указанному сигналу.

Воспользуемся результатами предыдущего примера для случая широко используемой на практике периодической последовательности импульсов, у которых длительность τ равна половине периода Т. Примем также t₁ = 0.

По формуле (1.32) определим постоянную составляющую, а по формулам (1.30) и (1.33) — амплитуды и фазы пяти первых гармоник. Данные расчетов сведены в табл. 1.1. Четные гармоники в табл. 1.1 не указаны, так как они равны нулю.

Таблица 1.1

Суммируя указанные составляющие, получим последовательность импульсов (рис. 1.8), отличающихся от прямоугольных в основном недостаточно высокой крутизной фронтов.

Отметим, что крутизна фронтов импульсов обусловлена наличием в их спектре составляющих с частотами, многократно превышающими основную частоту.

Распределение энергии в спектре. Рассмотрим, как распределяется энергия сложного периодического сигнала u(t) по его спектральным составляющим. Под временной функцией u(t) будем подразумевать электрическое напряжение на резисторе в 1 Ом. Энергия W_T, выделяемая на этом резисторе за время, равное периоду колебаний Т,

Используя спектральное представление u(t) в виде ряда Фурье (1.15), получим

Определим значения интегралов в выражении (1.35):

Так как A(jkw₁) и А(-jkw₁) комплексно сопряжены, то

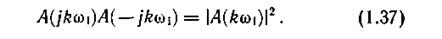
С учетом (1.28) и (1.29) выражение для W_T существенно упрощается:

Из (1.38) следует, что средняя за период энергия сложного периодического сигнала равна сумме средних энергий, выделяемых на резисторе в 1 Ом каждой его гармоникой в отдельности (включая постоянную составляющую).

С течением времени выделяемая энергия безгранично растет, при этом средняя мощность остается постоянной:

Важно отметить, что она не зависит от фаз отдельных гармоник и, следовательно, будет сохранять свое значение при изменениях формы сигнала, обусловленных нарушениями фазовых соотношений гармоник спектра.

Пример 1.3. Определим, какая часть средней мощности, выделяемой на резисторе с сопротивлением в 1 Ом, периодической последовательностью прямоугольных импульсов с параметрами из примера 1.2 приходится на пять первых гармоник и постоянную составляющую.

Значения амплитуд составляющих определены ранее (см. табл. 11). Подставляя их в (1.39), для средней мощности Р₅ сигнала, включающего указанные составляющие, получим

Так как средняя мощность последовательности прямоугольных импульсов при τ= Т/2 равна 0,5 , то искомая часть составляет 96% от этой мощности.

Область частот, в которой сосредоточена подавляющая часть мощности периодического сигнала, называют практической шириной его спектра. Если не предъявляется жестких требований относительно крутизны фронтов импульсов (см. пример 1 2), расширение этой области нецелесообразно.

Спектры непериодических сигналов. Любой физически реализуемый сигнал ограничен во времени и обладает конечной энергией. Функции, отображающие реальные сигналы, удовлетворяют условиям Дирихле и абсолютно интегрируемы, т. е.

где M — конечная величина.

Модели таких сигналов также могут быть представлены совокупностью гармонических составляющих в соответствии с выражением (1.2). Конкретный вид спектрального преобразования для непериодического сигнала получим, проследив изменения, происходящие в спектре периодической последовательности импульсов u₁(t) при увеличении периода их повторения.

В соответствии с формулой (1.30), которая справедлива для любого значения периода Т, абсолютные значения амплитуд спектральных составляющих в (1.27) при увеличении периода уменьшаются. Так как частоты составляющих спектра кратны основной частоте, то при ее уменьшении линии на спектральной диаграмме сближаются.

Спектральное представление для одиночного импульса u(t) получим как следствие увеличения периода сигнала u₁(t) до бесконечности.

Пару преобразований Фурье для периодической функции u₁(t) запишем в форме (1.15) и (1.16):

При T 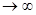u₁(t) переходит в u(t), частота ω₁ уменьшается до dw, а kw₁ превращается в текущую частоту ω. Заменяя суммирование интегрированием, находим

Обозначив интеграл в квадратных скобках S(jω), получим формулы для прямого и обратного интегрального преобразования Фурье:

Величину S(jω) называют комплексной спектральной плотностью или спектральной характеристикой. Она имеет размерность [амплитуда/частота]. На каждой конкретной частоте амплитуда соответствующей составляющей равна нулю. Сравнивая (1.15) и (1.42), находим, что бесконечно малому интервалу частоты dω соответствует составляющая с бесконечно малой комплексной амплитудой dA(jw):

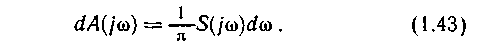
Сравнение выражения (1.41) для спектральной характеристики функции u(t), заданной на интервале времени , с формулой (1.17) для огибающей комплексного спектра такой же функции, периодически продолжающейся во времени, показывает, что они различаются только множителем:

Поэтому по известной спектральной характеристике одиночного импульса легко построить линейчатый спектр их периодической последовательности. Соотношением (1.44) объясняется и тот факт, что для различных представлений спектральной характеристики имеют место формулы, весьма похожие на (1.18) — (1.24).

Как комплексная величина спектральная характеристика может быть записана в виде

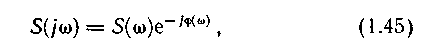
где S(ω)= |S(jω)| называется спектральной плотностью амплитуд или спектром непериодического сигнала.

Так как составляющие расположены на всех частотах, то спектр непериодического сигнала является непрерывным или сплошным. Представим спектральную характеристику состоящей из действительной и мнимой частей:

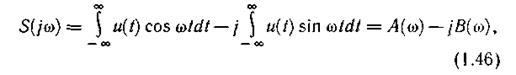
где

Модуль спектральной характеристики S(ω) определяется выражением

и представляет собой четную функцию частоты.

Для фазы спектральной характеристики S(jω) соответственно получаем

Так как из (1.42) и (1.43) следует, что A(ω) — четная функция частоты, а B(ω) — нечетная, то функция φ(ω) относительно частоты нечетна.

Комплексная форма интегрального преобразования Фурье легко приводится к тригонометрической:

Второй член в связи с нечетностью подынтегрального выражения равен нулю. Окончательно имеем

Преимущество тригонометрической формы записи Фурье-преобразования заключается в возможности некоторого физического толкования с использованием идеализации, не очень далеких от реальности.

Пример 1.4. Найти спектр одиночного прямоугольного импульса, описываемого функцией времени (рис. 1.9):

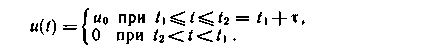
Выражение для спектральной характеристики амплитуд находим в соответствии с (1.41)

Искомый спектр представляет собой модуль этого выражения:

Спектр одиночного прямоугольного импульса (рис. 1.10), естественно [см. (1.44)], имеет ту же форму, что и огибающая периодической последовательности таких импульсов (см. рис. 1.6).

Пример 1.5. Определить спектр дельта-функции [см. соотношения (1.10) и рис. 1.3].

Запишем выражение для спектральной характеристики S_d(jw) дельта-функции, сосредоточенной в точке :

В соответствии с (1.11) имеем

откуда модуль спектральной характеристики

Следовательно, дельта-функции соответствует сплошной равномерный спектр, включающий в себя составляющие бесконечно больших частот (рис. 1.11). При ξι = 0 начальные фазы всех составляющих равны нулю.

Распределение энергии в спектре. Рассмотрим непериодический сигнал u(t), физическим представлением которого будем считать электрическое напряжение на резисторе с сопротивлением в 1 Ом.

Тогда энергия, выделяемая на этом резисторе

В предположении, что интеграл (1.54) сходится, выразим энергию через модуль спектральной характеристики S(ω) сигнала u(t). Квадрат этого модуля запишем в виде

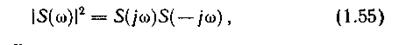
где

функция, комплексно-сопряженная спектральной характеристике S(jω) сигнала u(t). Тогда

После изменения последовательности интегрирования и использования обратного преобразования Фурье (1.42) получим

Окончательно имеем

Соотношение (1.56) известно как равенство Парсеваля. Оказывается, что энергию, выделяемую непериодическим сигналом за время его существования, можно определить, интегрируя квадрат модуля его спектральной характеристики в интервале частот.

Каждое из бесконечно малых слагаемых (1/π)|S(ω)|²dω, соответствующих бесконечно малым участкам спектра, характеризует энергию, приходящуюся на спектральные составляющие сигнала, сосредоточенные в полосе частот от ω до ω + dω.

§ 1.5. СООТНОШЕНИЯ МЕЖДУ ДЛИТЕЛЬНОСТЬЮ ИМПУЛЬСОВ И ШИРИНОЙ ИХ СПЕКТРОВ

Анализируя спектр одиночного прямоугольного импульса (см. рис. 1.10), можно установить, что при увеличении его длительности τ от 0 до спектр сокращается от безграничного (у дельта-функции) до одной спектральной линии в начале координат, соответствующей постоянному значению сигнала. Это свойство сокращения ширины спектра сигнала при увеличении его длительности и наоборот справедливо для сигналов любой формы. Оно вытекает непосредственно из особенностей прямого и обратного интегрального преобразования Фурье, у которых показатель степени экспоненциальной функции в подынтегральных выражениях имеет переменные t и ω в виде произведения.

Рассмотрим функцию u(t) определенной продолжительности и функцию u( t), длительность которой при λ>1 будет в λ раз меньше. Считая, что u(t) имеет спектральную характеристику S(jω), найдем соответствующую характеристику S (jω) для u( t):

где =λt.

Следовательно, спектр укороченного в λ раз сигнала ровно в λ раз шире. Коэффициент l/λ перед S(jω/λ) изменяет только амплитуду гармонических составляющих и на ширину спектра не влияет.

Другой важный вывод, также являющийся прямым следствием Фурье-преобразования, заключается в том, что длительность сигнала и ширина его спектра не могут быть одновременно ограничены конечными интервалами: если длительность сигнала ограничена, то спектр его неограничен, и, наоборот, сигнал с ограниченным спектром длится бесконечно долго. Справедливо соотношение

где Δt — длительность импульса; Δf — ширина спектра импульса; С — постоянная величина, зависящая от формы импульса (при ориентировочных оценках обычно принимают С=1).

Реальные сигналы ограничены во времени, генерируются и передаются устройствами, содержащими инерционные элементы (например, емкости и индуктивности в электрических цепях), и поэтому не могут содержать гармонические составляющие сколь угодно высоких частот.

В связи с этим возникает необходимость ввести в рассмотрение модели сигналов, обладающие как конечной длительностью, так и ограниченным спектром. При этом в соответствии с каким-либо критерием дополнительно ограничивается либо ширина спектра, либо длительность сигнала, либо оба параметра одновременно. В качестве такого критерия используется энергетический критерий, согласно которому практическую длительность Т_п и практическую ширину спектра w_п выбирают так, чтобы в них была сосредоточена подавляющая часть энергии сигнала.

Для сигналов, начинающихся в момент времени t₀ = О, практическая длительность определяется из соотношения

где η — коэффициент, достаточно близкий к 1 (от 0,9 до 0,99 в зависимости от требований к качеству воспроизведения сигнала).

Принимая во внимание равенство Парсеваля (1.56), для практической ширины спектра сигнала соответственно имеем

§ 1.6. СПЕКТРАЛЬНАЯ ПЛОТНОСТЬ МОЩНОСТИ ДЕТЕРМИНИРОВАННОГО СИГНАЛА

Величина , характеризующая распределение энергии по спектру сигнала и называемая энергетической спектральной плотностью, существует лишь для сигналов, У которых энергия за бесконечный интервал времени конечна и, следовательно, к ним применимо преобразование Фурье.

Для незатухающих во времени сигналов энергия бесконечно велика и интеграл (1.54) расходится. Задание спектра амплитуд невозможно. Однако средняя мощность Р_ср, определяемая соотношением

оказывается конечной. Поэтому применяется более широкое понятие «спектральная плотность мощности». Определим ее как производную средней мощности сигнала по частоте и обозначим Ρ_k(ω):

Индексом k подчеркивается, что здесь мы рассматриваем спектральную плотность мощности как характеристику детерминированной функции u(t), описывающей реализацию сигнала.

Эта характеристика сигнала менее содержательна, чем спектральная плотность амплитуд, так как лишена фазовой информации [см. (1.38)]. Поэтому однозначно восстановить по ней исходную реализацию сигнала невозможно. Однако отсутствие фазовой информации позволяет применить это понятие к сигналам, у которых фаза не определена.

Для установления связи между спектральной плотностью Ρ_k(ω) и спектром амплитуд воспользуемся сигналом u(t), существующим на ограниченном интервале времени (—T<.t<T). К такому сигналу применимо равенство Парсеваля (1.56). Из сравнения (1.62) с правой частью соотношения (1.56) следует

где — спектральная плотность мощности сигнала, ограниченного во времени.

В дальнейшем будет показано (см. § 1.11), что, усредняя эту характеристику по множеству реализаций, можно получить спектральную плотность мощности для большого класса случайных процессов.

§ 1.7. ФУНКЦИЯ АВТОКОРРЕЛЯЦИИ ДЕТЕРМИНИРОВАННОГО СИГНАЛА

Теперь в частотной области имеется две характеристики: спектральная характеристика и спектральная плотность мощности. Спектральной характеристике, содержащей полную информацию о сигнале u(t), соответствует преобразование Фурье в виде временной функции. Выясним, чему соответствует во временной области спектральная плотность мощности, лишенная фазовой информации.

Следует предположить, что одной и той же спектральной плотности мощности соответствует множество временных функций, различающихся фазами. Советским ученым Л. Я. Хинчиным и американским ученым Н. Винером практически одновременно было найдено обратное преобразование Фурье от спектральной плотности мощности:

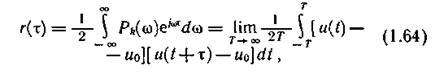
где

Обобщенную временную функцию r(t), не содержащую фазовой информации, назовем временной автокорреляционной функцией. Она показывает степень связи значений функции u(t), разделенных интервалом времени t, и может быть получена из статистической теории путем развития понятия коэффициента корреляции. Отметим, что во временной функции корреляции усреднение проводится по времени в пределах одной реализации достаточно большой продолжительности.

Справедливо и второе интегральное соотношение для пары преобразования Фурье:

Пример 1.6. Определить временную функцию· автокорреляции гармонического сигнала u(t) = u₀ cos(wt-φ). В соответствии с (1.64)

Проведя несложные преобразования

окончательно имеем

Как и следовало ожидать, r_u(t) не зависит от φ и, следовательно, (1.66) справедливо для целого множества гармоник, различающихся фазами.

§ 1.8. СЛУЧАЙНЫЙ ПРОЦЕСС КАК МОДЕЛЬ СИГНАЛА

Рассмотренные математические модели детерминированных сигналов являлись известными функциями времени. Их использование позволяет успешно решать задачи, связанные с определением реакций конкретных систем на заданные входные сигналы. Случайные составляющие, всегда имеющие место в реальном входном сигнале, считают при этом пренебрежимо малыми и не принимают во внимание.

Однако единственная точно определенная во времени функция не может служить математической моделью сигнала при передаче и преобразовании информации. Поскольку получение информации связано с устранением априорной неопределенности исходных состояний, однозначная функция времени только тогда будет нести информацию, когда она с определенной вероятностью выбрана из множества возможных функций. Поэтому в качестве моделей сигнала используется случайный процесс. Каждая выбранная детерминированная функция рассматривается как реализация этого случайного процесса.

Необходимость применения статистических методов исследования диктуется и тем, что в большинстве практически важных случаев пренебрежение воздействием помехи в процессах передачи и преобразования информации недопустимо. Считается, что воздействие помехи на полезный сигнал проявляется в непредсказуемых искажениях его формы. Математическая модель помехи представляется также в виде случайного процесса, характеризующегося параметрами, определенными на основе экспериментального исследования. Вероятностные свойства помехи, как правило, отличны от свойств полезного сигнала, что и лежит в основе методов их разделения.

Учитывая, что все фундаментальные выводы теории информации базируются на указанном статистическом подходе при описании сигналов (и помех), уточним основные характеристики случайного процесса как модели сигнала.

Под случайным (стохастическим) процессом подразумевают такую случайную функцию времени U(t), значения которой в каждый момент времени случайны. Конкретный вид случайного процесса, зарегистрированный в определенном опыте, называют реализацией случайного процесса. Точно предсказать, какой будет реализация в очередном опыте, принципиально невозможно. Могут быть определены лишь статистические данные, характеризующие все множество возможных реализаций, называемое ансамблем. Ценность таких моделей сигналов в том, что появляется возможность судить о поведении информационной системы не по отношению к конкретной реализации, а по отношению ко всему ансамблю возможных реализаций.

Основными признаками, по которым классифицируются случайные процессы, являются: пространство состояний, временной параметр и статистические зависимости между случайными величинами U(t_i) в разные моменты времени t_i.

Пространством состояний называют множество возможных значений случайной величины U(t_i). Случайный процесс, у которого множество состояний составляет континуум, а изменения состояний возможны в любые моменты времени, называют непрерывным случайным процессом. Если же изменения состояний допускаются лишь в конечном или счетном числе моментов времени, то говорят о непрерывной случайной последовательности.

Случайный процесс с конечным множеством состояний, которые могут изменяться в произвольные моменты времени, называют дискретным случайным процессом. Если же изменения состояний возможны только в конечном или счетном числе моментов времени, то говорят о дискретных случайных последовательностях.

Примеры реализаций указанных случайных процессов представлены на рис. 1.1.

Так как в современных информационных системах предпочтение отдается цифровым методам передачи и преобразования информации, то непрерывные сигналы с датчиков, как правило, преобразуются в дискретные, описываемые дискретными случайными последовательностями. Вопросы такого преобразования рассмотрены в гл. 2.