Глава 1 математические модели сигналов 2 страница

Прикладные результаты приводятся здесь только для пояснения основ теории. При более широкой трактовке теории информации результаты рассмотрения указанных вопросов составляют ее основу.

Если расширение связано с приложением теории в технике связи — рассмотрением проблемы разработки конкретных методов и средств кодирования сообщений, то совокупность излагаемых вопросов называют теорией информации и кодирования или прикладной теорией информации.

Другая точка зрения состоит в том, что глобальной проблемой теории информации следует считать разработку принципов оптимизации системы связи в целом. В этом случае к ней относят все локальные проблемы систем связи, включая, например, проблему оптимального приема и др.

В соответствии с третьей крайней точкой зрения к компетенции теории информации относят все проблемы и задачи, в формулировку которых входит понятие информации. Ее предметом считают изучение процессов, связанных с получением, передачей, хранением, обработкой и использованием информации. В такой постановке она затрагивает проблемы многих наук (в частности, кибернетики, биологии, психологии, лингвистики, педагогики) на всех трех уровнях (синтактическом, семантическом и прагматическом).

Попытки широкого использования идей теории информации в различных областях науки связаны с тем, что в основе своей эта теория математическая. Основные ее понятия (энтропия, количество информации, пропускная способность) определяются только через вероятности событий, которым может быть приписано самое различное физическое содержание. Подход к исследованиям в других областях науки с позиций использования основных идей теории информации получил название теоретико-информационного подхода. Его применение в ряде случаев позволило получить новые теоретические результаты и ценные практические рекомендации. Однако не редко такой подход приводит к созданию моделей процессов, далеко не адекватных реальной действительности. Поэтому в любых исследованиях, выходящих за рамки чисто технических проблем передачи и хранения сообщений, теорией информации следует пользоваться с большой осторожностью. Особенно это касается моделирования умственной деятельности человека, процессов восприятия и обработки им информации.

Содержание данной книги ограничивается теорией информации в первой трактовке, вопросами теории и практики кодирования и некоторыми примерами применения теории информации в областях, смежных с техникой связи.

Прикладная теория информации является одним из фундаментальных курсов при подготовке инженеров – системотехников, специализирующихся в области автоматизированных систем управления. Функционирование таких систем существенным образом связано с получением, подготовкой, передачей, хранением и обработкой информации, поскольку без осуществления этих этапов невозможно принять правильное решение, а следовательно, и осуществить требуемое управляющее воздействие, которое является конечной целью функционирования системы.

Контрольные вопросы

1. В чем сущность принципиальных различий в трактовке понятия информации?

2. Каковы основные этапы обращения информации?

3. Охарактеризуйте разновидности информационных систем и тенденции их развития.

4. Совокупность, каких объектов составляет систему передачи информации?

5. Что понимают под сообщением и сигналом?

6. В чем различие между линией и каналом связи?

7. Объясните разницу в уровнях проблем передачи информации.

8. Каковы основные задачи теории информации?

9. В чем сущность теоретико-информационного подхода к исследованиям?

ГЛАВА 1 МАТЕМАТИЧЕСКИЕ МОДЕЛИ СИГНАЛОВ

§ 1.1. ПОНЯТИЯ СИГНАЛА И ЕГО МОДЕЛИ

Как указывалось во введении, понятие «сигнал» имеет неоднозначное толкование. В широком смысле слова под сигналом понимают материальный носитель информации. При этом к сигналам относят как естественные сигналы, так и сигналы, специально создаваемые с определенной целью. Естественными являются, например, световые сигналы, позволяющие видеть окружающий мир, космические сигналы. Примером специально создаваемых могут служить сигналы, генерируемые с целью извлечения информации об изменениях в объекте или процессе (эталонные сигналы).

В дальнейшем понятие «сигнал», если это не оговорено специально, будет использоваться в узком смысле как сигнал, специально создаваемый для передачи сообщения в информационной системе. Материальную основу сигнала составляет какой-либо физический объект или процесс, называемый носителем (переносчиком) информации (сообщения). Носитель становится сигналом в процессе модуляции. Параметры носителя, изменяемые во времени в соответствии с передаваемым сообщением, называют информативными.

В качестве носителей информации используются колебания различной природы, чаще всего гармонические, включая частный случай — постоянное состояние (ω = 0). В технических информационных системах наиболее широкое распространение получили носители в виде электрического напряжения или тока. Поэтому, рассматривая в дальнейшем модели сигналов, для конкретности, будем соотносить их с электрическими сигналами.

В носителе u(t) = const имеется только один информативный параметр — уровень (например, уровень напряжения). При использовании гармонических электрических колебаний информативными могут стать такие параметры, как амплитуда, частота, фаза. Колебания принято подразделять на детерминированные и случайные.

Детерминированными называют колебания, которые точно определены в любые моменты времени.

Случайные колебания отличаются тем, что значения их некоторых параметров предсказать невозможно. Они могут рассматриваться как сигналы, когда несут интересующую нас информацию (случайные сигналы), или как помехи, когда мешают наблюдению интересующих нас сигналов.

При изучении общих свойств каналов связи, сигналов и помех мы отвлекаемся от их конкретной физической природы, содержания и назначения, заменяя моделями. Модель — это выбранный способ описания объекта, процесса или явления, отражающий существенные с точки зрения решаемой задачи факторы.

Задачи повышения эффективности функционирования информационных систем связаны с установлением количественных соотношений между основными параметрами, характеризующими источник информации и канал связи. Поэтому при исследовании используют математические модели. Математическое моделирование может быть реализовано различными методами в зависимости от способа, которым определяются интересующие нас показатели.

Фундаментальные исследования базируются на методе аналитического моделирования, заключающемся в создании совокупности математических соотношений, позволяющих выявить зависимости между параметрами модели в общем виде. При этом широко используются модели, параметры которых противоречат физическим свойствам реальных объектов. Например, модель сигнала часто представляется суммой бесконечного числа функций, имеющих неограниченную продолжительность (синусоид). Поэтому важно обращать внимание на условия, при которых это не мешает получать результаты, соответствующие наблюдаемым в действительности.

Так как источник сообщений выдает каждое сообщение с некоторой вероятностью, то предсказать точно изменения значения информативного параметра невозможно. Следовательно, сигнал принципиально представляет собой случайное колебание и его аналитической моделью может быть только случайный процесс, определяемый вероятностными характеристиками.

Тем не менее, в случае детерминированного колебания условно так же говорят о детерминированном сигнале. Такой сигнал отображает известное сообщение, которое нет смысла передавать. Ему соответствует модель в виде функции, полностью определенной во времени.

Изучение моделей детерминированных сигналов необходимо по многим причинам. Важнейшая из них заключается в том, что результаты анализа детерминированных сигналов являются основой для изучения более сложных случайных сигналов. Это обусловлено тем, что детерминированный сигнал может рассматриваться как элемент множества детерминированных функций, составляющих в совокупности случайный процесс. Детерминированное колебание, таким образом, представляет собой вырожденную форму случайного процесса со значениями параметров, известными в любой момент времени с вероятностью, равной единице. Детерминированные сигналы имеют и самостоятельное значение. Они специально создаются для целей измерения, наладки и регулирования объектов информационной техники, выполняя роль эталонов.

§ 1.2. ФОРМЫ ПРЕДСТАВЛЕНИЯ ДЕТЕРМИНИРОВАННЫХ СИГНАЛОВ

В зависимости от структуры информационных параметров сигналы подразделяют на дискретные, непрерывные и дискретно-непрерывные.

Сигнал считают дискретным по данному параметру, если число значений, которое может принимать этот параметр, конечно (или счетно). Если множество возможных значений параметра образует континуум, то сигнал считают непрерывным по данному параметру. Сигнал, дискретный по одному параметру и непрерывный по другому, называют дискретно-непрерывным.

В соответствии с этим существуют следующие разновидности математических представлений (моделей) детерминированного сигнала:

1. непрерывная функция непрерывного аргумента, например непрерывная функция времени (рис. 1.1, а);

2. непрерывная функция дискретного аргумента, например функция, значения которой отсчитывают только в определенные моменты времени (рис. 1.1,б);

3. дискретная функция непрерывного аргумента, например функция времени, квантованная по уровню (рис. 1.1, в);

4. дискретная функция дискретного аргумента, например функция, принимающая одно из конечного множества возможных значений (уровней) в определенные моменты времени (рис. 1.1, г).

Рассматриваемые модели сигналов в виде функций времени предназначены в первую очередь для анализа формы сигналов. Желательно найти такое представление сигнала, которое облегчает задачи исследования прохождения реальных сигналов, часто имеющих достаточно сложную форму, через интересующие нас системы. С этой целью сложные сигналы представляются совокупностью элементарных (базисных) функций, удобных для последующего анализа.

Наиболее широкий класс исследуемых систем — это инвариантные во времени линейные системы.

При анализе прохождения сложного сигнала u(t) через такие системы его представляют в виде взвешенной суммы базисных функций (t) (или соответствующего ей интеграла):

где [ , ] — интервал существования сигнала.

При выбранном наборе базисных функций сигнал u(t) полностью определяется совокупностью безразмерных коэффициентов . Такие совокупности чисел называют дискретными спектрами сигналов.

На интервале [t , t ] выражение (1.1) справедливо как для сигналов, неограниченных во времени, так и для сигналов конечной длительности. Однако за пределами интервала [t , t ] сигнал конечной длительности не равен нулю, так как он представляется суммой в том случае, если условно считается периодически продолжающимся. Поэтому, когда для ограниченного во времени сигнала необходимо получить представление, справедливое для любого момента времени, используется интеграл:

(1.2)

где φ(α, t) — базисная функция с непрерывно изменяющимся параметром .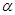

В этом случае имеется непрерывный (сплошной) спектр сигнала, который представляется спектральной плотностью S(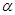). Размерность ее обратна размерности 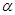. Аналогом безразмерного коэффициента здесь является величина S(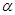)d .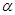

Совокупность методов представления сигналов в виде (1.1) и (1.2) называют обобщенной спектральной теорией сигналов. В рамках линейной теории спектры являются удобной аналитической формой представления сигналов.

Для теоретического анализа базисные функции нужно выбирать так, чтобы они имели простое аналитическое выражение, обеспечивали быструю сходимость ряда (1.1) для любых сигналов u(t) и позволяли легко вычислять значения коэффициентов . Базисные функции не обязательно должны быть действительными, их число может быть неограниченным .

В случае практической аппроксимации реального сигнала совокупностью базисных сигналов решающее значение приобретает простота их технической реализации. Сигнал представляется суммой ограниченного числа действительных линейно независимых базисных функций (сигналов).

Ортогональные представления сигналов. Вычисление спектральных составляющих сигнала существенно облегчается при выборе в качестве базиса системы ортогональных функций.

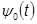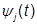Систему функций , (t),..., ,..., ,..., называют ортогональной на отрезке [t , t 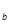], если для всех k = 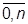; , за исключением случая k = j, удовлетворяется условие:

Эта система функций будет ортонормированной (ортонормальной), если для всех справедливо соотношение

Если соотношение (1.4) не выполняется и

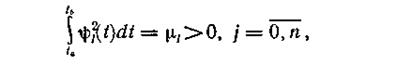
то систему можно нормировать, умножая функции 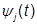на 1/ .

Определим коэффициенты при представлении сигнала u(t) совокупностью ортонормированных функций в виде

предполагая, что интервал [t , t ] лежит внутри отрезка ортогональности [t , t ].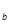

Правую и левую части уравнения (1.5) умножаем на 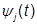и интегрируем, на интервале [t , t ]:

В силу справедливости условия (1.3) все интегралы в правой части выражения (1.6) при 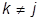будут равны 0. При k = j в соответствии с (1.4) интеграл равен 1. Следовательно,

В теоретических исследованиях обычно используют полные системы ортогональных функций, обеспечивающие сколь угодно малую разность непрерывной функции u(t) и представляющего ее ряда при неограниченном увеличении числа его членов. Разность оценивают по критерию

При этом говорят о среднеквадратической сходимости ряда к функции u(t).

Широко известной ортонормированной системой является совокупность тригонометрических функций кратных аргументов:

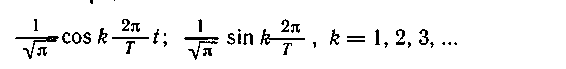
Она ортонормальна на отрезке [-π, π].Так как соответствующее разложение исторически появилось первым и было названо рядом Фурье, то соотношение (1.5) часто именуют обобщенным рядом Фурье, а значения - обобщенными коэффициентами Фурье.

На рис. 1.2 приведена система функций Хаара, ортонормированность которых на интервале 0-1 также очевидна. Известны представления сигналов по системам ортогональных базисных многочленов Котельникова, Чебышева, Лаггера, Лежандра и др., а также неортогональные разложения по функциям Лагранжа, Тейлора и др .

Обобщенная спектральная теория облегчает решение проблемы обоснованного выбора базисных функций для конкретных задач анализа процессов, происходящих при формировании и прохождении сигналов через те или иные звенья информационной системы.

§ 1.3. ВРЕМЕННАЯ ФОРМА ПРЕДСТАВЛЕНИЯ СИГНАЛА

Временным представлением сигнала называют такое разложение сигнала u(t), при котором в качестве базисных функций используются единичные импульсные функции — дельта-функции. Математическое описание такой функции задается соотношениями

где δ(t) — дельта-функция, отличная от нуля в начале координат (при t = 0).

Для более общего случая, когда дельта-функция отличается от нуля в момент времени t= (рис. 1.3), имеем

Такая математическая модель соответствует абстрактному импульсу бесконечно малой длительности и безграничной величины. Единственным параметром, правильно отражающим реальный сигнал, является время его действия. Однако, учитывая (1.10), с помощью дельта-функции можно выразить значение реального сигнала u(t) в конкретный момент времени ξι:

Равенство (1.11) справедливо для любого текущего момента времени t. Заменив ξι на t и приняв в качестве переменной интегрирования ξ, получим

Таким образом, функция u(t) выражена в виде совокупности примыкающих друг к другу импульсов бесконечно малой длительности. Ортогональность совокупности таких импульсов очевидна, так как они не перекрываются во времени.

Разложение (1.12) имеет большое значение в теории линейных систем, поскольку, установив реакцию системы на элементарный входной сигнал в виде дельта-функции (импульсную переходную функцию), можно легко определить реакцию системы на произвольный входной сигнал как суперпозицию реакций на бесконечную последовательность смещенных дельта-импульсов с «площадями», равными соответствующим значениям входного сигнала.

С помощью дельта-функций можно также представить периодическую последовательность идеализированных импульсов с постоянными или меняющимися уровнями. Обозначив через u (t) функцию, равную u(k t) в точках t = k t и нулю в остальных точках, запишем:

где Δt — период следования импульсов.

Поскольку умножение u(t) на дельта - функцию в момент времени t = k t соответствует получению отсчета этой функции, u_п(k t) может представлять результат равномерной дискретизации функции u(t).

§ 1.4. ЧАСТОТНАЯ ФОРМА ПРЕДСТАВЛЕНИЯ СИГНАЛА

Рассмотрим, какие функции целесообразно выбирать в качестве базисных при анализе инвариантных во времени линейных систем. При исследовании таких систем решения всегда содержат комплексные экспоненциальные функции времени. Детерминированные сигналы, описываемые экспоненциальными функциями времени, при прохождении через инвариантные во времени линейные системы не изменяются по своему характеру, что является следствием инвариантности класса экспоненциальных функций относительно операций дифференцирования и интегрирования.

Широко используются представления детерминированных сигналов с применением базисных функций е^pt как при ρ = (преобразование Фурье), так и при p = s+jw (обобщенное преобразование Фурье, известное как преобразование Лапласа).

До сих пор мы не касались физической интерпретации базисных функций. Для чисто математических преобразований она не обязательна. Однако такая интерпретация имеет безусловные преимущества, так как позволяет глубже вникнуть в физический смысл явлений, протекающих в системах при прохождении сигналов.

Использование экспоненциальных базисных функций в преобразовании Фурье комплексно-сопряженными парами (с положительным и отрицательным параметром ω) позволяет в соответствии с формулой Эйлера:

представить сложный детерминированный сигнал в виде суммы гармонических составляющих. Поскольку параметр ω в этом случае имеет смысл круговой частоты, результат такого преобразования называют частотной формой представления сигнала.

В силу указанных преимуществ разложение сигналов по системе гармонических базисных функций подверглось всестороннему исследованию, на основе которого была создана широко известная классическая спектральная теория сигналов.

В дальнейшем, если это не оговорено специально, спектральное представление сигналов рассматривается в рамках классической теории.

Спектры периодических сигналов. Периодических сигналов, естественно, не существует, так как любой реальный сигнал имеет начало и конец. Однако при анализе сигналов в установившемся режиме можно исходить из предположения, что они существуют бесконечно долго и принять в качестве математической модели таких сигналов периодическую функцию времени. Далее рассматривается представление таких функций, как в виде суммы экспоненциальных составляющих, так и с преобразованием их в гармонические.

Пусть функция u(t), заданная в интервале времени и удовлетворяющая условиям Дирихле, повторяется с периодом T = 2 / 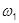= t₂-t₁ на протяжении времени от - до + .

Условия Дирихле: на любом конечном интервале функция должна быть непрерывной или иметь конечное число точек разрыва первого рода, а также конечное число экстремальных точек. В точках разрыва функцию u(t) следует считать равной.

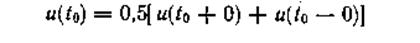
Если в качестве базисных выбраны экспоненциальные функции, то выражение (1.5) запишем в виде

Соотношение (1.15) представляет собой ряд Фурье в комплексной форме, содержащий экспоненциальные функции как с положительным, так и с отрицательным параметром ω (двустороннее частотное представление). Составляющие с отрицательными частотами являются следствием комплексной формы записи вещественной функции.

Функцию A(jkw₁) принято называть комплексным спектром периодического сигнала u(t). Этот спектр дискретный, так как функция A(jkw₁) определена на числовой оси только для целых значений k. Значение функции A(jkw₁) при конкретном k называют комплексной амплитудой.

Огибающая комплексного спектра A(jw) имеет вид

Запишем комплексный спектр в форме

Модуль комплексного спектра A(kw₁) называют спектром амплитуд, а функцию φ(kw₁) — спектром фаз.

Если известны спектр амплитуд и спектр фаз сигнала, то в соответствии с (1.15) он восстанавливается однозначно. В практических приложениях более значимым является спектр амплитуд, а информация о фазах составляющих часто несущественна.

Поскольку A(kw₁) и φ(kw₁) отличны от нуля только при целых k, спектры амплитуд и фаз периодического сигнала являются дискретными.

Воспользовавшись формулой Эйлера е ^-jkwt = coskwt - j sinkwt, выразим комплексный спектр A(jkw₁) в виде действительной и мнимой частей:

где

Спектр амплитуд

является четной функцией k, т.е.

Поскольку четность A_k и В_k, противоположна, спектр фаз

функция нечетная, т. е.

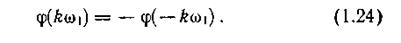
При k = 0 получаем постоянную составляющую

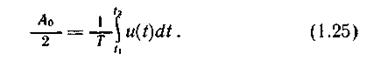
От двустороннего спектрального представления легко перейти к одностороннему (не имеющему отрицательных частот), объединяя комплексно-сопряженные составляющие [см. (1.14)]. В этом случае получаем ряд Фурье в тригонометрической форме. Действительно, выделив в (1.15) постоянную составляющую A₀/2 и суммируя составляющие симметричных частот ω и -ω, имеем