 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Математические и геометрические модели
|
|
Геометрический объект, изображение которого создается, как правило, можно представить через конечное множество базовых геометрических фигур, связанных между собой определенными соотношениями. Базовая геометрическая фигура – это фигура, рассматриваемая для данного геометрического объекта как неделимая составная часть с известными геометрическими параметрами. Любая базовая геометрическая фигура изображается с помощью точек, прямых, отрезков прямой, многоугольников, отрезков кривых, объемных фигур произвольных форм. Для отображения разнообразных свойств объектов (размеры, форма, положение в пространстве и др.) применяются разнообразные геометрические модели. Модели используются для представления реальных абстрактных предметов и явлений не только с целью формирования их изображений, но и в общем случае для представления их структуры и поведения. Они обеспечивают возможность имитации, проверки и предсказания поведения моделируемых явлений с целью понимания смысла, визуализации, экспериментирования и обучения. Будем рассматривать такие модели, которые пригодны для графической интерпретации. Среди обычных типов моделей, которые использует машинная графика, выделим следующие:
· организационные модели: структуры организаций, алгоритмов, классификаций;
· количественные модели: экономические; финансовые, социологические, демографические, климатические, химические, физические и математические системы;
· геометрические модели: технические и архитектурные конструкции, транспортные средства, молекулы и другие физические структуры.
С моделями необязательно должна ассоциироваться чисто геометрическая информация. А в тех случаях, когда в модели содержится чисто геометрическая информация, совершенно необязательно какое-либо конкретное представление этой геометрии в графическом виде, поскольку за пользователем остается право выбора точки зрения и проекции.
Наиболее важной проблемой является определение, какую геометрическую и негеометрическую информацию следует включать в модель и как ее представлять, кодировать. Среди составных частей, которые нужно учитывать в модели, можно назвать следующие:
· основные элементы данных и их взаимоотношения;
· пространственное размещение и форма компонент (геометрия объектов), а также информация о внешнем виде – цвет, фактура поверхности, раскраска;
· связность компонент (топология);с
· специфические для рассматриваемого применения данные (электрические или технические характеристики);
· обрабатывающие алгоритмы.
Таким образом, модель представляет собой описание компонент и процессов, которые совместно определяют структуру и поведение моделируемого объекта с заданной или возможной степенью адекватности.
Для отражения многообразных свойств объектов применяются различные геометрические модели: структурные, рецепторные, аналитические, каркасные составные.
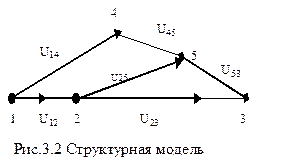 Структурные модели. В процедурах, относящихся к конструкторскому аспекту проектирования, преобладает использование моделей, отражающих только структурные свойства объекта – геоформу, размеры, взаимное расположение элементов в пространстве. Такие модели называются структурными.
Структурные модели. В процедурах, относящихся к конструкторскому аспекту проектирования, преобладает использование моделей, отражающих только структурные свойства объекта – геоформу, размеры, взаимное расположение элементов в пространстве. Такие модели называются структурными.
Структурные модели – это необходимая составная часть более подробных геометрических моделей, сложных геометрических объектов, состоящих из конечного числа базовых фигур и представляются графом. Наглядное представление о графе можно получить, если представить себе некоторое множество точек плоскости X, называемых вершинами, и множество направленных отрезков U, соединяющих все или некоторые из вершин и называемых дугами (рис. 3.3). Множество вершин (1, 2, 3, …) соответствует базовым геометрическим элементам, множество (U12, U23, …) ребер – связям между элементами. Граф может отражать, например, метрические свойства моделируемого объекта, поэтому его можно использовать для решения многих задач геометрического проектирования: разработки структурных и кинематических схем в задачах конструкторского и технологического синтеза; размещения и компоновки элементов различных конструкций.
 Рецепторные модели описывают геометрический объект в пространстве рецепторов. Область рецепторов формируется множеством сечений объекта, перпендикулярных координатным осям. В координатных осях получается прямоугольная решетка, каждая клетка которой рассматривается как отдельный рецептор, который может иметь состояние «0» или «1». Рецептор считается возбужденным (1), если он включается в контур плоской или пространственной области объекта. Плоский или пространственный геометрический объект можно описать двухмерной или трехмерной матрицей, состоящей из «0» и «1». Рецепторные модели могут описывать любые геометрические объекты, точность описания определяется количеством рецепторов. Например, модель приемника света представляет собой прямоугольный участок (рис. 3.3), разбитый без промежутков на I x J прямоугольных полей рецепторов со сторонами, параллельными сторонам участка. Расстояние между центрами соседних рецепторов вдоль оси X – c’, вдоль оси Y – d’, тогда номер рецептора, полю которого принадлежит точка изображения с координатами x, y
Рецепторные модели описывают геометрический объект в пространстве рецепторов. Область рецепторов формируется множеством сечений объекта, перпендикулярных координатным осям. В координатных осях получается прямоугольная решетка, каждая клетка которой рассматривается как отдельный рецептор, который может иметь состояние «0» или «1». Рецептор считается возбужденным (1), если он включается в контур плоской или пространственной области объекта. Плоский или пространственный геометрический объект можно описать двухмерной или трехмерной матрицей, состоящей из «0» и «1». Рецепторные модели могут описывать любые геометрические объекты, точность описания определяется количеством рецепторов. Например, модель приемника света представляет собой прямоугольный участок (рис. 3.3), разбитый без промежутков на I x J прямоугольных полей рецепторов со сторонами, параллельными сторонам участка. Расстояние между центрами соседних рецепторов вдоль оси X – c’, вдоль оси Y – d’, тогда номер рецептора, полю которого принадлежит точка изображения с координатами x, y
I = int(1 + I/2 – y/d’)
J = int(1 + J/2)+ x/c’)
При симметричном расположении рецепторов относительно осей координат последние выражения справедливы как для четного, так и для нечетного числа строк I и столбцов J.
Рецепторная модель может отображать и поле печатной платы интегральной схемы, покрытой системой соединений, в задачах трассировки соединений.
В тоже время эти модели требуют больших затрат памяти и времени на обработку.
Аналитические модели. Модели этого типа наиболее компактны и представляют собой описание ограничивающих контуров или поверхностей геометрической фигуры аналитическими уравнениями в полярной или прямоугольной системе координат.
Явная форма описание плоских кривых в координатах XY. Простейшим способом является явная форма описания y=f(x). Она удобна для описания и кривых, но не пригодна для проведения аналитических преобразований, когда функция неоднозначна.(Окружность, или кривая имеет вертикальные касательные. Например, прямая параллельная оси Y не имеет явного представления, так как производная df/dx=¥). Поэтому при геометрическом моделировании явная форма описания практически не применяется.
 От этих недостатков свободна неявная форма описания кривых f(x,y)=0. Например, для той же окружности уравнение будет иметь вид x2+y2-a2=0. Неявные уравнения кривых позволяют легко осуществлять аналитические преобразования и расчеты, но они не приспособлены для непосредственного вычисления точек на кривой и отображения их на плоскости, так как в общем случае приходится решать нелинейные уравнения итерационными способами.
От этих недостатков свободна неявная форма описания кривых f(x,y)=0. Например, для той же окружности уравнение будет иметь вид x2+y2-a2=0. Неявные уравнения кривых позволяют легко осуществлять аналитические преобразования и расчеты, но они не приспособлены для непосредственного вычисления точек на кривой и отображения их на плоскости, так как в общем случае приходится решать нелинейные уравнения итерационными способами.
Параметрическая форма описания позволяет решать проблему отображения кривых, описываемых неявно. Например, кривую на рисунке 3.4 можно представить как движение точки А, задаваемой вектором положения r, причем r является функцией времени, то есть r=r(t). Тогда путь задаваемый и пройденный точкой может быть любой кривой на плоскости. В координатной форме уравнения кривой будут иметь вид x=(t) и y = (t). В качестве параметра функции можно использовать любой скалярный параметр u. Для той же окружности параметрические уравнения можно записать в виде x=acost, y=asint, где t принимает значения от 0 до 2p., а уравнение прямой параллельной оси Y будет x=c,y=u., где u изменяется в пределах - ¥ < u <¥. Поскольку параметр измеряется произвольно, кривая не имеет единственного параметрического представления.
Аналитические модели широко применяются при подготовке управляющих программ для станков с ЧПУ, при проектировании геометрических объектов сложной формы, при раскрое материалов.
 Каркасные (кинематические) геометрические модели применяются при описании объемных фигур. Здесь рассматривают два способа реализации.
Каркасные (кинематические) геометрические модели применяются при описании объемных фигур. Здесь рассматривают два способа реализации.
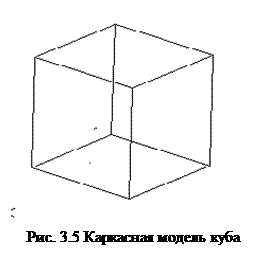 Первый способ получения каркасных моделей подразумевает, что поверхность образуется непрерывным перемещением линии, называемой образующей, в пространстве по некоторому закону. Образующая при перемещении пересекает ряд неподвижных линий, называемых направляющими. Наряду с направляющими могут использоваться условия параллельности, касания и другие отношения образующих с направляющими. Множество точек или линий, определяющих поверхность и принадлежащих ей, называется каркасом. В памяти ЭВМ при отображении поверхности на выходных графических устройствах она задается некоторым количеством линий, называемым дискретным каркасом поверхности (скелетной моделью поверхности)). На рисунке 3.5 приведена каркасная модель куба. Каркасная модель, как видно из рисунка, представляет собой скелетное описание трехмерного объекта. Она не имеет граней и состоит только из точек, отрезков и кривых, описывающих ребра объекта. Возможность создания каркасных моделей предоставляется в любом месте трехмерного пространства.
Первый способ получения каркасных моделей подразумевает, что поверхность образуется непрерывным перемещением линии, называемой образующей, в пространстве по некоторому закону. Образующая при перемещении пересекает ряд неподвижных линий, называемых направляющими. Наряду с направляющими могут использоваться условия параллельности, касания и другие отношения образующих с направляющими. Множество точек или линий, определяющих поверхность и принадлежащих ей, называется каркасом. В памяти ЭВМ при отображении поверхности на выходных графических устройствах она задается некоторым количеством линий, называемым дискретным каркасом поверхности (скелетной моделью поверхности)). На рисунке 3.5 приведена каркасная модель куба. Каркасная модель, как видно из рисунка, представляет собой скелетное описание трехмерного объекта. Она не имеет граней и состоит только из точек, отрезков и кривых, описывающих ребра объекта. Возможность создания каркасных моделей предоставляется в любом месте трехмерного пространства.
Второй способ получения каркасных поверхностей основан на понятии определителя поверхности. Совокупность условий, определяющих каркасную модель поверхности, называется определителем поверхности. Различают геометрическую и аналитическую части определителя. Геометрическая часть включает некоторое множество фигур, сохраняющих положение, форму и размеры. Аналитическая часть определителя представляет алгоритм построения точек и линий поверхности, занимающих в ней переменное положение. Например, сфера может быть образована вращением окружности около прямой, проходящей через центр окружности. В геометрическую часть определителя поверхности войдет уравнение окружности, а аналитическую – закон перемещения фигуры.
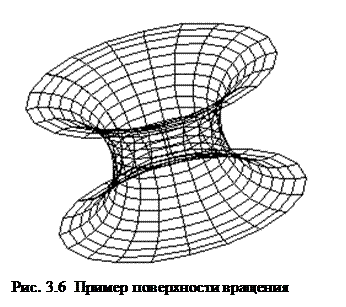 Частный случай каркасных моделей – модели поверхности вращения плоской кривой вокруг оси симметрии (рис. 3.6). Достаточно широкий класс машиностроительных деталей, предметов быта, архитектурных форм может быть представлен, как результат вращения кривой или ломаной линии относительно некоторой оси. Кривую линию, являющуюся линией вращения фигуры, аппроксимируют ломаной линией. Каждый отдельный участок последней становится образующей отдельного конуса, описание которого может быть как неявным, так и параметрическим в зависимости от алгоритма синтеза изображения.
Частный случай каркасных моделей – модели поверхности вращения плоской кривой вокруг оси симметрии (рис. 3.6). Достаточно широкий класс машиностроительных деталей, предметов быта, архитектурных форм может быть представлен, как результат вращения кривой или ломаной линии относительно некоторой оси. Кривую линию, являющуюся линией вращения фигуры, аппроксимируют ломаной линией. Каждый отдельный участок последней становится образующей отдельного конуса, описание которого может быть как неявным, так и параметрическим в зависимости от алгоритма синтеза изображения.
Таким образом, при построении каркасных моделей геометрических объектов используются аналитические модели линий и поверхностей, выраженные в форме параметрических уравнений.
Модели объемных объектов. В практике построения изображений объемных объектов широкое распространение получили три основных типа модели объектов:
· описание объекта поверхностями,
· сплошными телами;
· каркасные модели.
Первый подход представляет объект в виде тонких поверхностей, под которыми находится пустое пространство, не заполненное материалом объекта. Эллипсоид, рассматриваемый в рамках поверхностного описания, следует ассоциировать с неразбитой скорлупой совершенно пустого внутри яйца. Описания подобного типа достаточно часто встречаются в компьютерной графике, поскольку именно в рамках этого метода конструируют полигональные поля и бикубические поверхности.
Описание сплошными телами подразумевает, что объекту или отдельному примитиву принадлежат все точки объекта – как наружные, так и внутренние. В данном случае эллипсоид следует воспринимать как однородно заполненное тело – яйцо.
Описание типа проволочной сетки заключается в представлении поверхности серией пересекающихся линий, принадлежащих поверхности объекта.
Методы описания систем сплошными телами делят на три класса:
· основанные на пространственной декомпозиции объема, содержащего моделируемый объект, на массив участков или трехмерных ячеек, которые могут заполнить тело объекта; такие методы называются ячеечными или системами пространственного заполнения;
· объект представляется как комбинация простых форм примитивов, в качестве которых могут быть использованы кубы, шары, цилиндры. Сам же объект с точки зрения геометрической структуры может быть представлен древовидной структурой, терминальными вершинами которой являются примитивы. Такие модели называют моделями геометрических сплошных примитивов;
· системы, в которых объект задается границами. Здесь объект следует описывать состоящим из поверхностей конкретного типа, которые ограничены краями, часть краев является общей для нескольких поверхностей, края пересекаются в конкретных точках.
Ячеечные методы. Ограниченный участок пространства, охватывающий весь моделируемый объект, считается разбитым на большое число дискретных кубических ячеек. В простейшем случае размеры ребра куба равны единице измерения длины. Моделирующая система должна просто записать информацию о принадлежности или отсутствия таковой телу объекта. Структура данных представляется трехмерной матрицей, в которой каждый элемент соответствует пространственной ячейке. С одной стороны здесь все просто, а с другой – недостатки, связанные с большим объемом памяти, требуемой для описания объекта с большим разрешением.
Разработаны системы, которые используют идею разбиения ячеек на подъячейки меньшего размера. Последние применяются в случаях, когда ячейки захватывают границы объекта, и в целях повышения разрешения задействуют подъячейки, регулярно заполняющие ячейку границу.
Дата публикования: 2015-11-01; Прочитано: 3739 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
