Теза Черча. Зв'язок рекурсивних функцій з машинами Тьюрінга

Поняття частково-рекурсивної функції виявилося вичерпною формалізацією поняття обчислюваної функції. Ця обставина виражена у вигляді тези Черча, що є аналогом тези Тьюрінга для рекурсивних функцій: всяка функція, обчислювана деяким алгоритмом, частково-рекурсивна.

З зіставлення двох тез витікає твердження: функція обчислювана машиною Тьюрінга тоді і тільки тоді, коли вона частково-рекурсивна. Це затвердження про еквівалентність двох алгоритмічних моделей є (на відміну від тез) цілком точним математичним твердженням і, отже, потребує доведенння. Для доведення розіб'ємо його на дві теореми.

Теорема 5.6. Всяка частково-рекурсивна функція є обчислюваною на машині Тьюрінга.

План доведення ясний: спочатку доводиться, що найпростіші функції обчислювані (це досить очевидно), а потім – що оператори суперпозиції, примітивної рекурсії і m-оператор зберігають обчислюваність.

Обмежимося побудовою машини Тьюрінга для оператора примітивної рекурсії R_n. Для простоти позначень розглянемо випадок n=1. Нехай f(х, у)=R₁(g, h), тобто вона визначена схемою

f(х, 0)=g (х);

f(x, y+1)=h(x, у, f (х, у)),

де функції g і h обчислювані машинами T_g і Т_h відповідно, працюючими з правою напівстрічкою. Побудуємо машину Т_f, обчислюючу f. Машина T_f повинна відтворювати процес обчислення за схемою примітивної рекурсії, тобто послідовно обчислювати f(x,1)=h(x,0,f(x,0)),..., f(x,i+1)=h(x,i,f(x,i))... доти, поки не обчислить h(х, у, f(х, у)). Цей процес, що починається з конфігурації q₁1^x*1^y, розбивається на блоки, що виконують наступні дії (для кожного блоку вказана заключна конфігурація, що служить початковою для наступного блоку; стани не конкретизовані, а символ q вказує положення голівки):

1. Підготувати дані для обчислення g(х): О 1^x´1^y О q1^x.

2. Обчислити g(х) на правій напівстрічці: О 1^x´1^y О q1^g(x).

3. Перевірити, що у=0. Якщо так, тоді блок 7. Якщо ні, тоді блок 4.

4. Підготувати дані для обчислення h(х, i, f(х, i)) і записати 1 в крайній зліва пустий осередок (тобто додати 1 до числа зліва від початкових даних, виділених маркерами О): 1ⁱ⁺¹О1^x´1^y Оq1^x ´ 1ⁱ ´1^f(x,i).

5. Обчислити h на правій напівстрічці 1ⁱ⁺¹О1^x´1^y Оq1^{h(x, i, f(x, i))}.

6. Перевірити, чи вірно, що у=i+l. Якщо так, тоді блок 7. Якщо ні, то блок 4.

7. Видати результат (стерти все зліва від q, повернутися назад і зупинитися).

Блок 2 реалізовується машиною T_g, блок 5 - машиною Т_h. Побудова блоків 1, 3, 6, 7 очевидна. Блок 4 зсуває число 1^{h(x, i-1, f(x, i-1))}=1^{f(x, i)}, отримане на попередньому кроці блоком 5, на х+i+2 клітки праворуч і записує в пропуск, що звільнився, слово 1^x´1ⁱ´ (число 1ⁱ дорівнює числу, записаному на початку роботи блоку 4 зліва від початкових даних). Схожий процес здійснювався за допомогою машини Т_пер при побудові універсальної машини Т, тому на деталях зупинятися не будемо.

Таким чином, машина T_f, що реалізує оператор примітивної рекурсії для n=1, побудована. Для n> 1 все залишається таким же, збільшується лише число змінних і, відповідно, маркерів у векторах початкових даних f, g і h. Реалізация трьох рекурсивних операторів дозволяє за рекурсивним описом будь-якої частково-рекурсивної функції (представленням її у вигляді кінцевої послідовності застосувань операторів 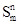,R_n і m до найпростіших функцій) побудувати машину Тьюрінга, що її реалізовує.

Теорема 5.7. Всяка функція, обчислювана на машині Тьюрінга, частково-рекурсивна.

Переходимо до доведення теореми 5.7. Спочатку опишемо арифметизацію машин Тьюрінга. Як вже вказувалося, символи на стрічці інтерпретуються як m-ічні цифри (наприклад, в порядку їх переліку в алфавіті, тобто a_i кодується цифрою i). При цьому символу l завжди ставиться у відповідність 0. Оскільки непустих символів на стрічці в будь-який момент кінцеве число, то угода дозволяє мати справу тільки з кінцевими числами. Для визначеності (і простоти позначень) при ілюстраціях будемо вважати, що A={1, l}, замість l будемо писати 0. Стану q_i машини поставимо у відповідність число i; літерою z визначимо код заключного стану; зсуви закодуємо так: R=1, L=0 (як було показано в § 4.2, випадок з Е можна не розглядати). Символи стрічки, стани і зсуви не будемо відрізняти від їх кодів. Система команд машини Т з множиною станів Q і алфавітом А перетворюється при такому кодуванні в трійку числових функцій: j_q:Q´A®Q (функція наступного стану), j_a:Q´A®A (функція символа, що друкується), j_d:Q´A®{0, 1} (функція зсуву). Якщо S_Т містить команду q_ia_j®q_ia_jd_k, то j_q(q_i, a_j)=q_i; j_a(q_i, a_j)=a_j; j_d(a_i, a_j)=d_k. Зазначимо, що всі ці функції задані на кінцевій множині q´a і, отже, є примітивно-рекурсивними.

Кожній конфігурації aq_ia_jb однозначно ставиться у відповідність четвірка чисел (), що визначаються таким чином: 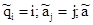– число, що зображається цифрами, отриманими кодуванням символів слова аналогічно виходить з b, але при цьому читається з права наліво, тобто найлівіший осередок β містить самий молодший розряд, а крайній праворуч – самий старший (це зроблено для того, щоб нулі праворуч від b не впливали на значення). Наприклад, конфігурації 10110q₅11011 відповідає четвірка (22, 5, 1, 13). Виконання команди перетворює конфігурацію К в наступну конфігурацію К', при арифметизації цьому відповідає перетворення четвірки в нову четвірку (). Наприклад, при команді q₅1®q₃0R раніше наведена конфігурація перейде в К'=101100q₃1011, якій відповідає четвірка (44, 3, 1, 6). Тому один крок машини Т однозначно визначає відображення множини конфігурацій в себе, тобто нечислову функцію y_T(K)=K'. Назвемо її функцією наступного кроку. При введеній арифметизації цій функції відповідає четвірка числових функцій наступного кроку; інакше кажучи, – це числові функції, кожна з яких залежить від чотирьох числових змінних . Ці функції досить простим образом пов'язані з функціями системи команд j_q, j_a, j_d. Дійсно, q'=j_q, інші функції залежать ще і від зсуву. Якщо голівка зсунулася праворуч, то це означає зсув цифр на розряд ліворуч, тобто збільшення числа в m разів (нагадаємо, що m – потужність алфавіту А), і зсув цифр числа на розряд праворуч (оскільки вони читаються з права наліво), тобто зменшення числа в m разів. Крім того, в молодший розряд записується символ, надрукований на даному кроці, а молодший розряд стає символом, що оглядається. При зсуві голівки ліворуч ролі і міняються; меншає, збільшується і т.д. Тому

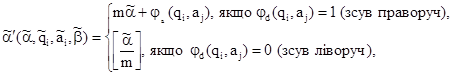(5.5-а)

(5.5-б)

(5.5-в)

(5.5-г)

Функції [ ] і r, використані тут, визначені в прикладі 5.11. Оскільки функції 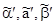побудовані з примітивно-рекурсивних функцій за допомогою примітивно-рекурсивного оператора умовного переходу, а функція просто співпадає з примітивно-рекурсивною функцією j_q, то всі вони – примітивно-рекурсивні функції від чотирьох змінних . Можна пересвідчитися, що застосування співвідношень (5.5) до наведеної раніше як приклад четвірки (22, 5, 1, 13) і команди q₅1®q₃0R дасть четвірку (44, 3, 1, 6); нагадаємо, що m=2.

Отже, доведено, що на кожному кроці будь-яка машина Тьюрінга здійснює примітивно-рекурсивне обчислення. Переходимо тепер до арифметизації загальної поведінки машини.

Нехай задана початкова конфігурація K(0)=(). Тоді конфігурація, виникаюча на такті t, залежить від величини t і компонент початкової конфігурації, інакше кажучи, вона є векторною функцією K(t)=(K_a(t), K_q(t), K_a(t), K_b(t)), компоненти якої - векторні функції, що залежать від п'яти змінних t, . Ці функції визначаються таким чином:

(5.6-а)

У співвідношеннях (5.6-б)-(5.6- г) аргументи в функціях K_i для скорочення опустимо:

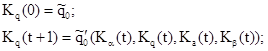(5.6-б)

(5.6-в)

(5.6-г)

Співвідношення (5.6) формально виражають ту очевидну обставину, що координати вектора K(t+1) однозначно визначаються координатами вектора K(t). Ці співвідношення являють собою схему примітивної рекурсії, що визначає чотири функції K_a, K_q, K_a, K_b (рекурсія ведеться за змінною t) за допомогою функцій , примітивна рекурсивність яких вже доведена. Отже, функції Ki також примітивно-рекурсивні.

Залишився останній крок доведення: рекурсивний опис результату роботи машини Тьюрінга. Обмежимося для простоти правильно обчислюючими машинами (які починають з конфігурацій виду q₁a₀b₀ і зупиняються в конфігураціях виду q_za_zb_z). Для таких машин K_a=0, K_q=1, початкове слово на стрічці кодується числом , заключне слово – числом . Тому результат роботи машини – це функція . Заключне слово – це слово, написане на стрічці в той момент, коли машина уперше перейшла в заключний стан q_z, тобто в момент t_z=mt(K(t)=z). Тому і . Якщо надати f стандартний вигляд f(х), враховуючи при цьому, що , і виписати всі аргументи функції К, отримуємо:

(5.7)

(m, z - константи, що залежать від конкретної машини), звідки безпосередньо видно, що функція f, що описує результат роботи машини Тьюрінга, побудована з примітивно-рекурсивних функцій за допомогою оператора m і, отже, є частково-рекурсивною.

З теорем 5.6, 5.7 і співвідношень (5.7) слідує теорема Кліні про нормальну форму:

Теорема 5.8. Будь-яка частково-рекурсивна функція f(х) представима у вигляді:

f(x)=F(my[G(x,y)=0]),

де F і G - примітивно-рекурсивні функції.

Таким чином, клас частково-рекурсивних функцій виявився еквівалентним класу функцій, що обчислюються машинами Тьюрінга. Еквівалентність цих класів, в основі побудови яких лежали абсолютно різні підходи, непрямим образом підтверджує справедливість тез Черча та Тьюрінга і дозволяє об'єднати їх в одну тезу Черча - Тьюрінга. Крім того, вона дає можливість формулювати основні результати теорії алгоритмів в більш загальному вигляді.