Деякі операції над машинами Тьюрінга

Робота машини Тьюрінга повністю визначається початковими даними і системою команд. Однак для розуміння того, як конкретна машина розв’язує дану задачу, як правило, виникає потреба в змістовних поясненнях типу тих, які приводилися для машини Т_коп. Ці пояснення часто можна зробити більш формальними і точними, якщо використати блок-схеми і деякі операції над машинами Тьюрінга.

Нагадаємо, що композицією двох функцій f₁(х) і f₂(у) називається функція g(х)=f₂(f₁(х)), яка виходить при застосуванні f₂ до результату обчислення f₁. Для того, щоб g(х) була визначена при даному х, необхідно і досить, щоб f₁ була визначена на х, і f₂ була визначена на f₁(х).

Теорема 5.1. Якщо f₁(х) і f₂(у) обчислювані за Тьюрінгом, тоді їх композиція f₂(f₁(х)) також обчислювана за Тьюрінгом.

Нехай Т₁ – машина, що обчислює f₁, а Т₂ - машина, що обчислює f₂, і множини їх станів відповідно Q₁= 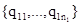і Q₂= 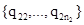. Побудуємо діаграму переходів машини Т з діаграм Т₁ і Т₂ таким чином: ототожнимо початкову вершину q₂₁ діаграми машини Т₂ з кінцевою вершиною q_1z діаграми машини T₁ (для систем команд це рівносильно тому, що систему команд T₂ приписуємо до системи команд T₁ і при цьому q_1z в командах T= замінюємо на q₂₁). Отримаємо діаграму з n₁+n₂-1 станами. Початковим станом Т оголосимо q₁₁, а заключним - q_2z. Для простоти позначень будемо вважати f₁ і f₂ числовими функціями однієї змінної.

Нехай f₂(f₁ (х)) визначена. Тоді T₁(1^x)=1 і q₁₁1^x q_1z1 .Машина Т пройде ту ж послідовність конфігурацій з тією різницею, що замість q_1z1 вона перейде в q₂₁1 . Ця конфігурація є стандартною початковою конфігурацією для машини Т₂, тому q₂₁1 q_2z1 . Але оскільки всі команди Т₂ містяться в Т, то q₁₁1^x Þq₂₁1 Þ q_2z1 і, отже, T(1^x)=1 . Якщо ж f₂(f₁(х)) не визначена, тоді Т₁ або Т₂ не зупиниться і, отже, машина Т не зупиниться. Отже, машина Т обчислює f₂(f₁(х)).

Мал. 5.6.

Побудовану таким чином машину Т будемо називати композицією машин T₁ і T₂ і означати T₂(T₁), а також зображати блок-схемою (мал. 5.6.). Ця блок-схема має більш точне значення, ніж зображена на мал. 5.3, оскільки вона завжди передбачає, що початковими даними машини T₂ є результати T₁. При цьому вони вже «готові до вживання», оскільки завдяки правильній обчислюваності (яка істотна при композиції) заключна конфігурація T₁ легко перетворюється в стандартну початкову конфігурацію T₂.

Оскільки машина Тьюрінга вектор над А_вих сприймає як слово в алфавіті А_вихÈ{*}, визначення композиції і теорема 5.1 залишаються в силі, якщо T₁ і Т₂ обчислюють функції від декількох змінних. Важливо лише, щоб дані для T₂ були в зумовленому вигляді підготовлені машиною T₁. Це видно на наступному прикладі.

Приклад 5.8. Машина, діаграма якої наведена на мал. 5.7, це машина Т₊Т_коп. Вона обчислює функцію f(х)=2x для х¹0; при цьому машина Ткоп будує двохкомпонентний вектор, а Т+ обчислює функцію від двох змінних.

Для зручності подальших побудов встановимо наступний важливий факт. Виявляється, що для обчислення на машині Тьюрінга досить, щоб стрічка була нескінченною тільки в одну сторону, наприклад праворуч. Така стрічка називається правою напівстрічкою.

Теорема 5.2. Будь-яка функція, обчислювана за Тьюрінгом, обчислювана на машині Тьюрінга з правою напівстрічкою; інакше кажучи, для будь-якої машини Тьюрінга Т існує еквівалентна їй машина TR з правою напівстрічкою. Аналогічна теорема формулюється для лівої напівстрічки.

Мал. 5.7

Можна передбачити принаймні дві ідеї побудови такої еквівалентної машини: 1) кожного разу, коли голівці колишньої машини треба зайти за лівий край стрічки, нова машина заздалегідь зсуне все написане (разом з голівкою) на клітку праворуч; б) стрічка «перегинається навпіл»; при цьому осередки правої половини колишньої стрічки розміщуються, скажемо, в непарних осередках напівстрічки, а осередки лівої половини - в парних. Перша ідея реалізована в [3]; реалізація другої пропонується як вправа.

Розглянемо тепер обчислення предикатів на машинах Тьюрінга. Машина Т обчислює предикат Р(a) (a– слово в А_вих), якщо Т(a)=w, де w=І, коли Р(a) є істинним, і w=П, коли Р(a) є помилковим. Якщо ж Р(a) не визначений, тоді машина Т, як і при обчисленні функцій, не зупиняється. При звичайному обчисленні предиката знищується a, що може виявитися незручним, якщо після Т повинна працювати інша машина. Тому введемо поняття обчислення з відновленням: машина Т обчислює Р(a) з відновленням, якщо T(a)=wa. Якщо існує машина Т,що обчислює Р(a), то існує і ,що обчислює Р(a) з відновленням. Дійсно, обчислення з відновленням можна представити наступною послідовністю конфігурацій: q₁aÞq_n1a*aÞa*q_n2aÞa*q_n3wÞq_n4wa. Перша частина цієї послідовності реалізовується машиною Т_коп, друга - простим зсувом головки до маркера*, третя - машиною T_R, що обчислює Р(a) на правій напівстрічці (одного копіювання мало для відновлення, оскільки копію може зіпсувати основна машина Т, тому потрібна машина, що не заходить ліворуч від a), четверта - перенесенням w в крайнє ліве положення. Машина Т є композицією вказаних чотирьох машин. Однак в конкретних випадках можливі і більш прості способи відновлення a.

Приклад 5.9. Машина з діаграмою на мал. 5.8 обчислює предикат «a – парне число»: голівка досягає кінця числа в стані q₂, якщо число одиниць парне, і в стані q₃, якщо число одиниць непарне, після чого вона переміщується в початкове положення в стані q₄ або q₅ і друкує І або П відповідно. Для того, щоб цей предикат обчислювався з відновленням, досить в петлях q₄ і q₅ не стирати, а зберігати одиниці, тобто замінити команди 1®lL на команди 1®L.

Мал. 5.8.

Оскільки машина Тьюрінга з алфавітом А_вих={І, П} і командами q₁І®q_zПЕ і q₁П®q_zІЕ обчислює заперечення логічної змінної, то з обчислюваності всюди визначеного Р(a) слідує обчислюваність .

Нехай функція f(a) задана описом: «якщо Р(a) істинне, тоді f(a) =g1(a), інакше f(a) =g₂(a)» (під «інакше» мається на увазі «якщо Р(a) помилкове»; якщо ж Р(a) не визначене, то f(a) також не визначена). Функція f(a) називається розгалуженням або умовним переходом до g₁(a) і g₂(a) за умови Р(a).

Теорема 5.3. Якщо g₁ (a), g₂ (a) і Р (a) обчислювані за Тьюрінгом, то розгалуження g₁ і g₂ по Р також є обчислюваним.

Нехай T₁ – машина з станами і системою команд å₁, обчислююча g₁; T₂ - машина з станами і системою команд å₂, обчислююча g₂; T_p – обчислює з відновленням P(a). Тоді машина Т, обчислююча розгалуження g₁ і g₂ по Р, це композиція T_p і машини Т_з, система команд å₃ якої має наступний вигляд:

å₃=å₁Èå₂È{q₃₁І®lq₁₁R, q₃₁П®lq₂₁R, q_1z®q_2zE}.

Перші дві з нових команд передають управління системам команд å₁ або å₂ в залежності від значення предиката P(a). Третя команда введена для того, щоб T₃ мала один заключний стан q_2z. Відсутність символа стрічки в цій команді означає, що вона виконується при будь-якому символі.

Розгалуження зустрічається в структурі діаграм переходів багатьох машин Тьюрінга.

Приклад 5.10-а. У прикладі 5.6.-а було описано побудову машини Т₊ для складання двох чисел. На мал. 5.8 наведена діаграма машини Т₊₊ для складання n чисел (n=1, 2...). Цикл з станів q₁, q₂, q₃ - це «зациклена» машина Т_+, в якій заключний стан суміщений з початковим. Сума, отримана на черговому циклі, є першим доданком наступного циклу. Стан q₄ реалізує розгалуження. У ньому перевіряється умова - чи є другий доданок. Якщо так (про що говорить наявність маркера *), тоді відбувається перехід до наступного циклу; якщо немає (про що говорить (після одиниць), то машина виходить з циклу.

Мал. 5.9

б. Нехай машина Т з алфавітом А_Т і з А_вих={1} не є правильно обчислюючою й її заключна конфігурація стандартна, але може містити будь-які символи з А_Т (крім пропусків), а результат інтерпретується як число, що дорівнює числу одиниць на стрічці. Побудуємо для Т машину Т'_++, яка працює як Т_++, а всі символи, крім 1 і l, вона сприймає як маркери, тобто команди для них ті ж, що і для *. Тоді T'₊₊ збере всі одиниці в один масив і, отже, T^'₊₊(T(a)) правильно обчислює функцію, що обчислюється машиною Т. Приклад 5.10 ілюструє важливий окремий випадок розгалуження - вихід з циклу за умови, добре відомий в програмуванні. У словесних описах (див. приклад 5.1.) і в багатьох мовах програмування (наприклад, в АЛГОЛі) цей випадок формулюється так: повторювати обчислення f₁ доти, поки є істинною умова Р, якщо Р помилкова, перейти до обчислення f₂.

Завдяки обчислюваності композиції і розгалуження словесні описи і мову блок-схем можна зробити цілком точною мовою для опису роботи машин Тьюрінга. Кожний блок - це множина станів, в якій виділені початковий і заключний стани, і система команд. Правильне обчислення для проміжних блоків не обов'язкове, тому при стиковці блоків важливо погоджувати всю конфігурацію. Перехід до блоку – це обов'язково перехід в його початковий стан. Машина Тьюрінга, що описується блок-схемою, – це об'єднання станів і команд, що містяться у всіх блоках. Зокрема, блоком може бути один стан. Блоки,що обчислюють предикати, позначимо літерою Р.

Приклад 5.11. На мал. 5.10 наведена блок-схема машини Тьюрінга T_x, що здійснює множення двох чисел: T_x(1^a*1^b)=1^ab. Її заключний стан - q₀₃. Блоки реалізують наступні вказівки і обчислення:

Р₁ – обчислити з відновленням предикат «обидва доданки більші нуля»;

Т₁ – стерти всі непусті символи праворуч;

Т₂ – встановити голівку в осередку, наступному (праворуч) за маркером * '; маркер * замінити на ~, Т_коп - див. приклад 6.6-б, в якому команду q₁l®q_zR треба замінити на команду q₁~®q_zR;

Т_коп (а - 1) разів копіює 1b; після i-го циклу вона зупиняється в конфігурації 1a-i-1(~1b)i-1~q1b * 1b;

T₃ - повернути голівку до крайнього зліва непустого символа. Після (а - 1)-го циклу цим символом виявиться ~ (або *, якщо а=1), і відбувається вихід з циклу і перехід до .

працює як Т₊₊ (див. приклад 10.a) з тією різницею, що числа, які вона підсумовує, розділені двома видами маркерів: ~ і *; для цієї мети в неї до команд з маркером * в лівій частині додані такі ж команди для маркера ~.

Аналогічно тому, як з машини Т₊ була побудована Т_++, можна з Т_х побудувати машину Т_хх, яка перемножує декілька чисел, і за схемою, аналогічною наведеній на мал. 5.10, з використанням T_xx замість побудувати машину, що здійснює возведення до ступеня. Інший важливий приклад, який читач може або побудувати, або знайти в [2, 3], – переклад унарного представлення чисел в позиційне двійкове або десятеричне.

Мал. 5.10.

Універсальна машина Тьюрінга. Систему команд машини Тьюрінга можна інтерпретувати і як опис роботи конкретного механізму і як програму, тобто сукупність розпоряджень, що однозначно приводять до результату. При розборі прикладів будь-який читач мимовільно приймає другу інтерпретацію, виступаючи в ролі механізму, який здатний відтворити роботу будь-якої машини Тьюрінга. Упевненість в тому, що все це будуть робити однаково (якщо не нароблять помилок, що, до речі, передбачається і при роботі машини Тьюрінга), - це по суті упевненість в існуванні алгоритму відтворення роботи машини Тьюрінга за заданою програмою, тобто системою команд. Дійсно, словесний опис такого алгоритму дати неважко. Його основна дія, що циклічно повторюється, полягає в наступному.

«Для поточної конфігурації a₁a_rq_ia_ja₂ знайти в системі команд команду з лівою частиною q_ia_j. Якщо права частина цієї команди має вигляд q_i^'a^'_jR, то замінити в поточній конфігурації q_ia_j на a_j^'q_i^' (вийде конфігурація a₁a_ra_j^'q_i^'a₂); якщо ж права частина має вигляд q_i^'a_j^'L, то замінити a_rq_ia_j на q_i^'a_ra_j^' (як видно з прикладу 5.5, випадок з Е можна не розглядати)».

Як вже говорилося в § 5.1, словесний опис алгоритму може бути неточним і потребувати формалізації. Оскільки в якості такої формалізації поняття алгоритму зараз обговорюється машина Тьюрінга, то природно поставити задачу побудови машини Тьюрінга, що реалізує описаний алгоритм відтворення. Для машини Тьюрінга, що обчислює функції від однієї змінної, формулювання цієї задачі таке: побудувати машину Тьюрінга U, яка обчислює функцію від двох змінних, і таку, що для будь-якої машини Т з системою команд å_T U(å_T,a)=T(a), якщо T(a) визначнена (тобто U(å_T,a) зупиняється, якщо машина Т зупиняється при початкових даних a, і U(å_T,a) не зупиняється, якщо Т(a) не зупиняється). Будь-яку машину U, що має вказану властивість, будемо називати універсальною машиною Тьюрінга. Неважко узагальнити це формулювання на будь-яке число змінних.

Перша проблема,що виникає при побудові універсальної машини U, пов'язана з тим, що U, як і будь-яка інша машина Тьюрінга, повинна мати фіксований алфавіт A_U і фіксовану множину станів Q_U. Тому систему команд å_T і початкові дані довільної машини Т не можна просто переписати на стрічку машини U (завжди знайдеться машина Т, алфавіти A_T і Q_T якої перевершують за потужністю A_U і Q_U, або просто не співпадають з ними). Вихід полягає в тому, щоб символи з A_T і Q_T кодувати словами в алфавіті A_U. Нехай |A_T|=m_T, |Q_T|=n_T. Будемо завжди вважати, що a₁=1, =l (ці два символи завжди є в алфавіті будь-якої машини, яка працює з числами). Визначимо коди q_i і a_j через S(q_i) і S(q_j) і визначимо їх таким чином: S(l)= , для будь-якого іншого a_i S(a_i)= a 1ⁱ, для заключного стану q_Tz S(q_Tz)=q , S(q_i)=q 1ⁱ, якщо i¹n_T. Код S(a_j) для даної машини Т завжди має довжину (формат) m_T, а код S(q_i) - формат n_T. Символи R,L,® введемо в A_U, тобто S(R)=R, S(L)=L, S(®)=®. Код слова a, утворений кодами символів, що складають це слово, визначимо S(a). Таким чином, остаточне уточнення постановки задачі про універсальну машину U зводиться до того, що для будь-якої машини Т і слова a в алфавіті A_TU(S(å_T),S(a))=T(a).

План побудови машини U такий. Будемо вважати, що машина Т завжди працює на правій напівстрічці (строго кажучи, це припущення порушує спільність міркувань, незважаючи на теорему 5.2, адже на довільній системі команд å_T не написано, працює вона з правою напівстрічкою чи ні). Однак теорема 5.2 містить алгоритм перетворення в систему команд для роботи з правої напівстрічкою. Виходячи з нього, можна побудувати машину Тьюрінга Т_пр, що реалізує цей алгоритм, і розглядати універсальну машину U(T_пр(å_T),a)). Тоді стрічку U можна розділити на дві нескінченні напівстрічки з кордоном Z між ними: в правої напівстрічці записується поточна конфігурація машини Т (внаслідок нашого припущення конфігурація машини Т при цій імітації ніколи не зайде на ліву напівстрічку), а в лівої напівстрічці записаний код системи команд S(å_T). Зокрема, початкова конфігурація U має вигляд: u₁S(å_T)ZS(q₁)S(a) (u₁– початковий стан машини U, q₁ – початковий стан Т, a – початкове слово Т). Наприклад, початковій конфігурації машини з прикладу 5.3, а з початковим словом 11 відповідає наступне слово на стрічці машини U:

q1a1®q1a1Rq1ll®q1a1RZq1a1a1.

Виконанню однієї команди Т відповідає цикл машини U, що реалізує основну дію, описану раніше, з тією різницею, що вона буде здійснюватися не над конфігурацією К машини Т, а над її кодом S(К). Завдяки обраному кодуванню довжини всіх слів виду S(q_ia_j) і S(a_jq_i) рівні, тому при замінах S(q_ia_j) на S(a_j^'q_i^') або S(a_rq_i) на S(q_i^'a^'_j), що імітують рушення голівки машини Т, околиця слів, що замінюються, не зачіпається і ніяких зсувів або розсувів не потрібно. Сама довжина слова, що замінюється, дорівнює числу символів між ® і найближчим символом руху (R або L) на лівій напівстрічці.

Опишемо більш детально роботу машини U, розбивши опис на кроки (блоки).

1. Для слова S(q_i,a_j) на правій напівстрічці (його початок - єдиний на правій напівстрічці символ q, а кінець відстоїть від q на число символів, що дорівнює формату S(q_ia_j)) з'ясувати, чи є в лівій напівстрічці слово S(q_ia_j)®. Якщо так, то перейти до кроку 2. Якщо такого слова немає, то перейти до кроку 10.

2. У знайденому слові S(q_ia_j) замінити ®на *.

3. З'ясувати, чи дорівнює R найближчий символ руху праворуч від *. Якщо так, перейти до кроку 4, якщо ні, то до кроку 7.

4. У m_T осередків правої напівстрічки, що починаються з q, записати слово довжиною mT, що починається з (n_T+1)-го символа правіше * (це слово має вигляд S(a_j') і є кодом символа, який машина Т друкує по команді q_ia_j®q_i^'a_j^'R. Після записаного слова надрукувати мітку ||.)

5. У n_T осередків правої напівстрічки, що починаються із ||, записати слово довжиною nT, що починається безпосередньо праворуч від А (це слово має вигляд S(q_i') і є кодом стану, в який машина Т переходить по команді q_ia_j®q_i^'a_j^'R).Внаслідок кроків 4 і 5 слово S(q_ia_j) на правій напівстрічці замінюється словом S(a_j^'q_i^'), що імітує команду q_ia_j®q_i^'a_j^'R.

6. Замінити в правій напівстрічці * на ® і перейти до кроку 1.

7. Слово довжиною mT, розташоване на правій напівстрічці безпосередньо зліва від q, зсунути праворуч на n_T кліток. Після зсунутого слова надрукувати мітку ||.

8. У m_T осередків правої напівстрічки, що починаються із ||, записати слово довжиною mT, що починається з (n_T+1)-го символа правіше * (це слово має вигляд S(a_j') і є кодом символа, який машина Т друкує по команді q_ia_j®q_i^'a_j^'L. В клітці, розташованій на m_T+n_T кліток лівіше початку записаного слова, надрукувати ||.)

9. У n_T осередків правої напівстрічки, що починаються із ||, записати слово довжиною nT, що починається безпосередньо праворуч від * (це слово має вигляд S(q_i') і є кодом стану, в який машина Т переходить по команді q_ia_j®q_i^'a_j^'L). Перейти до кроку 6.

10. Внаслідок кроків 7, 8, 9 слово S(a_rq_ia_j) на правій напівстрічці замінюється словом S(q_i^'a_ra_j^'), що імітує команду q_ia_j®q_i^'a_j^'L.

11. Стерти в правій напівстрічці код стану (цей стан буде заключним для Т, оскільки перехід 1 до кроку 10 означає, що стан машини Т не зустрівся в лівих частинах команд машини Т) і зупинитися. При цьому заключна конфігурація буде мати вигляд: S(åT)Zl...luzb, де uz - заключний стан U, а b - код результату Т, тобто b=S(Т(a)).

Мал. 5.11

Блок-схема U, що відповідає цьому опису, наведена на мал. 5.11. Її цикл реалізує основну дію алгоритму відтворення роботи машини Т, причому гілка циклу 3 4 5 6 відповідає зсуву голівки Т праворуч, а гілка 3 7 8 9 6 - зсуву голівки ліворуч.

Наведений раніше опис роботи машини U зовні нічим не відрізняється від словесного опису в прикладі 5.1, однак насправді воно набагато точніше. У ньому повністю уточнені представлення даних і їх розташування в пам'яті. Для того, щоб зробити цей опис абсолютно точним, тобто перетворити в систему команд машини U, залишається показати, що блоки цього опису можуть бути реалізовані машинами Тьюрінга. Для кроків 2, 3, 6, 10 це є очевидним. Для реалізації інших кроків побудуємо спочатку машину Т_пер, яка слово, розташоване між мітками «і», переписує на місце, що починається з мітки || (передбачається, що мітки «,», || зустрічаються на стрічці по одному разу, причому || лежить правіше). Блок-схема машини Тпер з алфавітом А_вих=={a₁,..., a_m, «,», ||} і m допоміжними символами b₁,..., b наведена на мал. 5.12.

Мал. 5.12

Всі машини Т₁,..., Т_m мають по п'ять станів. У випадку, коли перший ще не переписаний символ лівого слова дорівнює a_i, він замінюється на b₁, тобто позначається як переписаний, і управління передається машині T_i, яка йде праворуч, проходить всі вже виписані символи (тобто символи b_j) правого слова, праворуч (а на першому проході замість мітки ||) від них пише символ b_i, і повертається ліворуч до першого ще не переписаного символа лівого слова. Якщо цим символом виявляється мітка «, то перезапис скінчений, і управління передається машині T_m+1_, яка стирає всі мітки, тобто замінює b_i на a_i, і зупиняється. Система команд машини Т_i (i=1,..., m) наведена в табл. 5.5,що утримує 2m+2 рядка. Система команд T_m+1 є очевидною і тут не наводиться.

Кроки 4,5,8,9 реалізуються безпосередньо за допомогою машини Т_пер, роботі якої повинно передувати розставляння міток «і». Положення цих міток відлічується від початкової мітки *, поставленої на кроці 2, за допомогою форматів m_T і n_T, величина яких витягується з коду системи команд, точніше з лівої частини коду самої правої команди: стан в ній не може бути заключним і має код виду q 1ⁱ, тому число символів (кліток) між другим праворуч символом руху і кінцем масиву одиниць дорівнює n_T. Число символів, що залишилося до стрілки ®, дорівнює m_T.

Крок 1 реалізується за допомогою зациклювання модифікованої машини Т'_пер, в якій слово, відмічене мітками «, «, знаходиться правіше за мітку ||, а машини Т_i працюють з права наліво і при цьому не переписують, а порівнюють, тобто перевіряють, чи не є рівним a_i перший з невідмічених символів лівого слова. Робота Т'_пер продовжується доти, поки або цим символом виявиться ® (це означає, що потрібна команда знайдена), або до a_j¹a_i, після чого мітка || пересувається в початок наступної ліворуч команди і знов включається Т'_пер.

Таблиця 5.5.

	qi1	qi2	qi3	qi4
a1	qi1R	qi3biL	qi3L	qi4L
×	×	×	×	×
×	×	×	×	×
×	×	×	×	×
am	qi1R	qi3biL	qi3L	qi4L
>>	qi1R	–	qi4L	–
½||½	qi3b1L	–	–	–
B1	qi2R	qi2R	qi3L	qizR
×	×	×	×	×
×	×	×	×	×
×	×	×	×	×
Bm	qi2R	qi2R	qi3L	qizR

Нарешті, крок 7 реалізується за допомогою іншої модифікації Т''_пер, в якій дозволяється, щоб мітка || знаходилася між «і». Її побудова надається читачеві.

На цьому побудова універсальної машини U закінчується.

Зазначимо, що при побудові U (як, проте, і для багатьох інших машин, описаних в цьому параграфі) ми не переслідували цілі оптимізації і не жаліли ні символів стрічки, ні станів, прагнучи до наглядності побудови. Неважко показати, що можна побудувати машину U всього з двома символами на стрічці. Шеннон встановив менш очевидний факт: він побудував універсальну машину з двома станами. У той же час показано (Боброу і Мінський), що універсальна машина з двома станами і двома символами неможлива. Взагалі в визначених межах зменшення числа символів U веде до збільшення числа станів і навпаки. Докладне зведення результатів про мінімальні універсальні машини наведене в [2].

Існування універсальної машини Тьюрінга означає, що систему команд å_Т будь-якої машини Т можна інтерпретувати таким чином: або як опис роботи конкретного пристрою машини Т, або як програму для універсальної машини U. Для сучасного інженера, що проектує систему управління, ця обставина цілком природна. Він добре знає, що будь-який алгоритм управління може бути реалізований або апаратно - побудовою відповідної схеми, або програмно - написанням програми для універсальної керуючої ЕОМ. Однак важливо усвідомлювати, що сама ідея універсального алгоритмічного пристрою абсолютно не пов'язана з розвитком сучасних технічних засобів його реалізації (електроніки, фізики твердого тіла і т.д.) і є не технічним, а математичним фактом, що описується в абстрактних математичних термінах, які не залежать від технічних засобів, і до того ж що спирається на надто малу кількість вельми елементарних початкових понять. Характерно, що базові роботи з теорії алгоритмів (і, зокрема, роботи Тьюрінга) з'явилися в 30-х роках, набагато раніше за створення сучасних ЕОМ.

Вказана інтерпретація зберігає на абстрактному рівні основні плюси і мінуси двох варіантів інженерної реалізації. Конкретна машина Т працює набагато швидше; крім того, керуючий пристрій машини U досить громіздкий (тобто велике число станів і команд). Однак його складність постійна, і, будучи раз побудованим, він годиться для реалізації яких завгодно великих алгоритмів, знадобиться лише більший об'єм стрічки, яку природно вважати більш дешевою і більш просто влаштованою, ніж керуючий пристрій. Крім того, при зміні алгоритму не знадобиться будувати нових пристроїв; треба лише написати нову програму.

Теза Тьюрінга. Досі нам вдавалося для всіх процедур, що претендують на алгоритмічність, тобто конструктивних процедур, будувати реалізуючі їх машини Тьюрінга. Чи буде це вдаватися завжди? Ствердна відповідь на це питання міститься в тезі Тьюрінга, яка формулюється так: «Всякий алгоритм може бути реалізований машиною Тьюрінга». Довести тезу Тьюрінга не можна, оскільки саме поняття алгоритму (або ефективної процедури) є неточним. Це не теорема і не постулат математичної теорії, а твердження, яке зв'язує теорію з тими об'єктами, для опису яких вона створена. По своєму характеру теза Тьюрінга нагадує гіпотези фізики про адекватність математичних моделей фізичним явищам і процесам. Підтвердженням тези Тьюрінга є, по-перше, математична практика, а по-друге, та обставина, що опис алгоритму в термінах будь-якої іншої відомої алгоритмічної моделі може бути зведений до його опису у вигляді машини Тьюрінга. Теза Тьюрінга дозволяє, з одного боку, замінити неточні твердження про існування ефективних процедур (алгоритмів) точними твердженнями про існування машин Тьюрінга, а з другого боку, твердження про неіснування машин Тьюрінга тлумачити як твердження про неіснування алгоритмів взагалі. Однак не треба розуміти тезу Тьюрінга в тому значенні, що вся теорія алгоритмів може бути зведена до теорії машин Тьюрінга. Наприклад, в теорії складності алгоритмів (що швидко розвивається зараз і яка розглядає порівняльну складність алгоритмів по пам'яті, числу дій і т.д.) результати, вірні в рамках однієї алгоритмічної моделі (скажімо, про число дій, необхідних для обчислення даної функції), можуть виявитися невірними в іншій моделі.

Проблема зупинки. У числі загальних вимог, що пред'являються до алгоритмів (див. § 5.1), згадувалася вимога результативності. Найбільш радикальним формулюванням тут була б вимога, щоб за будь-яким алгоритмом А і даними a можна було визначити, чи приведе робота А при початкових даних a до результату чи ні. Інакше кажучи, треба побудувати алгоритм В, такий, що В(А, a)=І, якщо А(a) дає результат, і В (А, a) =П, якщо А(a) не дає результату. Внаслідок тези Тьюрінга цю задачу можна сформулювати як задачу про побудову машини Тьюрінга: побудувати машину Т₀, таку, що для будь-якої машини Тьюрінга Т і будь-яких початкових даних для машини T₀(å_T,a)=І, якщо машина Т(a) зупиняється, і T₀(å_T,a)=П_, якщо машина Т(a) не зупиняється.

Ця задача називається проблемою зупинки. Її формулювання дещо нагадує задачу про побудову універсальної машини і, зокрема, також передбачає вибір відповідного кодування å_Т і a в алфавіті машини Т₀. Однак в цьому випадку ніяке кодування не приводить до успіху.

Теорема 5.4. Не існує машини Тьюрінга Т₀, що вирішує проблему зупинки для довільної машини Тьюрінга Т.

Припустимо, що машина Т₀ існує. Для певності будемо вважати, що маркером між å_Т та a на стрічці машини Т₀ служить *. Побудуємо машину Т₁(å_Т)=Т₀(Т_коп(å_Т)). Початковими даними машини Т₁ є системи команд (точніше, їх коди) будь-якої машини Т. Запис å_Т на стрічці машина Т₁ перетворює в å_Т*å_Т (машина Т_коп для чисел описана в прикладі 5.6-б), а потім працює як машина Т₀. Таким чином, Т₁ також вирішує проблему зупинки для будь-якої машини Т, але тільки в тому випадку, коли на стрічці Т в якості даних a_Т написана її власна система команд å_Т. Інакше кажучи, Т₁(å_Т)=І, якщо машина Т(å_Т) зупиняється, і Т₁(å_Т)=П, якщо машина Т(å_Т) не зупиняється. Нехай q_1n – заключний стан T₁. Додамо до системи команд T₁ один стан q_{1, n+1}, оголосивши його заключним, і m команд (m-число символів T₁) q_1nП®q_1,n+1Е, q_1na_j®q_1nR для будь-якого a_j; (в тому числі І), крім П. Отримаємо машину T^'₁(å_T), яка зупиняється, якщо Т не зупиняється, і не зупиняється, якщо Т зупиняється. Запишемо тепер на стрічці машини T₁' її власну систему команд. Тоді T'₁ зупиниться, якщо вона не зупиняється, і не зупиниться, якщо вона зупиняється. Очевидно, така машина T'₁ неможлива. Але оскільки вона отримана з T₀ цілком конструктивними засобами, які не викликають сумнівів, і при цьому ніяк не пов'язана з конкретною структурою машини T₀, залишається зробити висновок, що ніяка машина T₀, що вирішує проблему зупинки, неможлива.

Внаслідок тези Тьюрінга неможливість побудови машини Тьюрінга означає відсутність алгоритму розв'язання даної проблеми. Тому отримана теорема дає перший приклад алгоритмічно нерозв'язної проблеми, а саме, алгоритмічно нерозв'язною виявляється проблема зупинки для машин Тьюрінга, тобто проблема визначення результативності алгоритмів.

При тлумаченні тверджень, пов'язаних з алгоритмічною нерозв'язністю, потрібно мати на увазі наступну важливу обставину. У таких твердженнях мова йде про відсутність єдиного алгоритму, що вирішує дану проблему; при цьому зовсім не виключається можливість розв'язань цієї проблеми в окремих випадках, але різними засобами для кожного випадку. Зокрема, теорема 6.4 не виключає того, що для окремих класів машин Тьюрінга проблема зупинки може бути розв’язана (однак існують конкретні машини Тьюрінга (наприклад, будь-яка універсальна машина) з нерозв'язною проблемою зупинки). Наприклад, вона вирішується для всіх машин, наведених в прикладах 5.3-5.10. Тому нерозв'язність загальної проблеми зупинки зовсім не знімає необхідності доводити сходимість алгоритмів, що пропонуються, а лише показує, що пошук таких доведень не можна повністю автоматизувати.

Нерозв'язність проблеми зупинки можна інтерпретувати як неіснування загального алгоритму для відладки програм, точніше, алгоритму, який за текстом будь-якої програми і даними для неї визначав би, чи зациклиться програма на цих даних чи ні. Якщо врахувати зроблене раніше зауваження, така інтерпретація не суперечить тому емпіричному факту, що більшість програм зрештою вдається налагодити, тобто встановити наявність зациклення, знайти його причину і усунути її. При цьому вирішальну роль грають досвід і мистецтво програміста.