Примітивно-рекурсивні функції. Визначення і приклади

Займемося тепер конкретним вибором засобів, за допомогою яких будуть будуватися обчислювані функції. Очевидно, що до обчислюваних функцій потрібно віднести всі константи, тобто 0 і всі натуральні числа 1, 2, 3... Однак в прямому включенні нескінченної множини констант в базис немає необхідності. Досить однієї константи 0 і функції проходження f(х)=х+1, яку іноді означають x', щоб отримати весь натуральний ряд. Крім того, в базис включимо сімейство {Iⁿ_m} функцій тотожності (або введення фіктивних змінних):

Iⁿ_m(x₁,...,x_n)=x_m(m£n).

Вельми могутнім засобом отримання нових функцій з тих, що вже існують, є суперпозиція, знайома нам з розділів 3 і 4. В них суперпозицією називалася будь-яка підстановка функцій в функції. Тут їй для більшої наглядності зручно надати стандартний вигляд. Оператором суперпозиції Sⁿ_m називається підстановка в функцію від m змінних m функцій від n одних і тих же змінних. Вона дає нову функцію від n змінних. Наприклад, для функцій

h(x₁,...,x_m),g₁(x₁,...,x_n),...,g_m(x₁,...,x_n)

Sⁿ_m(h,g₁,...,g_m)=h(g₁(x₁...x_n),...,g_m(x₁,...,x_n))=f(x₁,...,x_n).

Це визначення породжує сімейство операторів суперпозиції { Sⁿ_m}. Завдяки функціям тотожності стандартизація суперпозиції не зменшує її можливостей: будь-яку підстановку функцій в функції можна виразити через Sⁿ_m. Наприклад, f(x₁,x₂)=h(g₁(x₁x₂),g₂(x₁))в стандартному вигляді запишеться як f(x₁x₂)= S²₂(h(x₁x₂),g₁(x₁x₂),S¹₂(I²₁(x₁x₂),g₂(x₁),g₃(x₁))), де g₃ – будь-яка функція від x₁. У свою чергу, використовуючи підстановку і функції тотожності, можна переставляти і ототожнювати аргументи в функції:

f(x₂,x₁,x₃,...,x_n)=f(I²₂(x₁,x₂), I²₁(x₁,x₂),x₃,...,x_n);

f(x₁,x₁,x₃,...,x_n)=f(I²₁(x₁,x₂), I²₁(x₁,x₂),x₃,...,x_n).

Таким чином, якщо задані функції Iⁿ_m і оператори Sⁿ_m, то можна вважати заданими всілякі оператори: підстановки функцій в функції, а також перейменування, перестановки і ототожнення змінних.

Ще одне сімейство операторів, яке тут знадобиться, це оператори примітивної рекурсії. Оператор примітивної рекурсії R_n визначає (n+1)-місцеву функцію f через n-місцеву функцію g і (n+2)-місцеву функцію h таким чином:

(5.2.)

Пара рівностей (5.2) називається схемою примітивної рекурсії. Той факт, що функція визначена схемою (5.2), виражається рівністю f(x₁,...,x_n,y)=R_n(g,h). У випадку, коли n=0, тобто функція, що визначається f, є одномісною, схема (5.2) набуває більш простого вигляду:

f(0)=c; f(y+1)=h(y,f(y)), (5.3).

де с – константа.

Схеми (5.2) і (5.3) визначають f рекурсивно не тільки через інші функції g і h, але і через значення f в попередніх точках: значення f в точці у+1 залежить від значення f в точці у. Для обчислення f(x₁,..., x_n, r) знадобиться r+1 обчислень за схемою (5.2) для у=0, 1,..., r.

Приклад такого визначення функції: n!=(n-1)!n. Істотним в операторі примітивної рекурсії є те, що незалежно від числа змінних в f рекурсія ведеться тільки за однією змінною у; інші n змінних x₁,..., x_n на момент застосування схем (5.2), (5.3) зафіксовані і грають роль параметрів.

Функція називається примітивно-рекурсивною, якщо вона може бути отримана з константи 0, функції x' і функцій Iⁿ_m за допомогою кінцевого числа застосувань операторів суперпозиції і примітивної рекурсії. Цьому визначенню можна додати більш формальний індуктивний вигляд.

1. Функції 0, x' і Iⁿ_m для всіх натуральних n, m, де m£n, є примітивно-рекурсивними.

2. Якщо g₁(x₁,...,x_n),...,g_m(x₁,...x_n),h(x₁,...,x_m) примітивно-рекурсивні функції, то Sⁿ_m(h,g₁,..,g_m)– примітивно-рекурсивні функції для будь-яких натуральних n, m.

3. Якщо g(x₁,...,x_n) и h(x₁,..,x_n,y,z) примітивно-рекурсивні функції, то R_n(g, h) – примітивно-рекурсивна функція.

4. Інших примітивно-рекурсивних функцій немає. З такого індуктивного опису неважко витягнути процедуру, породжуючу всі примітивно-рекурсивні функції.

Приклад 5.12. (складання, множення, возведення до ступеня).

1. Складання f₊(x,y)=x+y примітивно-рекурсивне:

f₊(x,0)=x=I¹₁(x);

f₊(x,y+1)= f₊(x,y)+1= (f₊(x,y))'.

2. Таким чином, f₊(x,y)=R₁(I¹₁(x),h(x,y,z)), де h(x,y,z)=z^'=z+1.

Множення f_x(x,y)=xy примітивно-рекурсивне:

fx(х, 0)=0;

f_x(x,y+1)=f_x(x,y)+x=f₊(x,f_x(x,y)).

3. Возведення до ступеня f_exp(x,y)=xy примітивно-рекурсивне:

f_exp(x,0)=1;

f_exp(x,y+1)=x^yx=f_x(x,f_exp(x,y)).

Визначимо функцію х у (арифметичне або урізане віднімання) таким чином:

Приклад 5.13. (віднімання). Примітивно-рекурсивними є наступні функції:

1) f(х)=х 1, що визначається схемою:

f(0)=0 1=0;

f(у+1)=у;

2) f(х, у)=х у що визначається схемою:

f(х, 0)=х;

f(х, у+1)=х (у+1)=(х у) 1=f(х, у) 1;

(для визначення функції з п. 2 використана функція з п. 1);

3) f(x,y)=|x-y|=(x y)+(y-x);

4) sg(x)=

її схема має вигляд:

sg(0)=0;

sg(x+1)=1;

5) min(x,y)=x (x y);

6) max(x,y)=y+(x y).

За допомогою функції sg (сігнум) з прикладу 5.10 і її заперечення (х)=1 sg х побудуємо примітивно-рекурсивний опис функцій, пов'язаних з поділом.

Приклад 5.14 ( поділ).

1) Функція r(х, у) - залишок від поділу у на х:

r(x,0)=0;

r(x,y+1)=(r(x,y)+1)sg(|x-(r(x,y)+1)|).

Значення другого рядка визначення в наступному: якщо у+1 не ділиться на х, то sg(|x (r(x,y)+1)|)=1 й r(x,y+1)=r(x,y) +1; якщо ж у+1 ділиться на х, то r(x,y+1)=sg(|x-(r(x,y)+1)|)=0.

2) Функція q(х, у)=[у/х] - частка від поділу у на х, тобто ціла частина дробу у/х:

q(х, 0)=0;

q(x,y+1)=q(x,y)+ (|x-(r(x,y)+1|).

Другий доданок, як і у випадку r(х, у), залежить від дільності у+1 на х. Якщо у+1 ділиться на х, то q(х, у+1) на одиницю більше, ніж q(х, у), якщо ні, то q(х, у+1)=q(х, у).

У рекурсивних описах функцій прикладу 5.14 виразно видно логічні дії: перевірка умови (дільність у+1 на х) і вибір подальшого ходу обчислень в залежності від істинності умови. Займемося тепер більш докладним з'ясуванням того, які можливості для логічних операцій є в рамках примітивно-рекурсивних функцій.

З функцій прикладів 5.13-2),5),6) легко виходить примітивна рекурсивность «арифметизованих» логічних функцій, тобто числових функцій, які на множині {0, 1} поводяться як логічні функції. Дійсно, якщо х, ує{0,1}, то

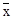=1 x;

xÚy=max(x,y); (5.4)

x&y=min(x,y).

З функціональної повноти (див. § 3.6) цієї множини функцій і того, що суперпозиція є примітивно-рекурсивним оператором (див. далі), слідує примітивна рекурсивность всіх логічних функцій.

Відношення R(x₁,..., x_n) називається примітивно-рекурсивним, якщо примітивно-рекурсивна його характеристична функція c_R:

У зв'язку з взаємно однозначною відповідністю між відносинами і предикатами c_R буде характеристичною функцією і для відповідного предикату.

Нагадаємо, що сам предикат приймає логічні значення І і П, з якими не можна виконувати арифметичних дій, навіть коли ці значення зображаються числами 0 і 1. Тому потрібно провести відмінність між предикатами та їх характеристичними функціями. У алгоритмічних мовах типу АЛГОЛ предикат буде приймати значення true і false, а його характеристична функція - значення 0 і 1. Предикат називається примітивно-рекурсивним, якщо його характеристична функція примітивно-рекурсивна. Внаслідок співвідношень (5.4), якщо предикати P₁,..., P_r примітивно-рекурсивні, то і будь-який предикат, отриманий з них за допомогою логічних операцій, примітивно-рекурсивний.

Приклад 5.15. (предикати і відносини).

1) Предикат Pd_n(x)²x ділиться на n² примітивно-рекурсивний для будь-якого n: c_Pdn(x)= (r(n,x)).

2) Предикат Pd_n,m(x) ²x ділиться на m і на n» примітивно-рекурсивний для будь-яких m і n, оскільки P_m,n(x)=P_m(x)&P_n(x).