Тема: «Дифференциальное и интегральное исчисление. Неопределенный и определенный интегралы и их свойства

Применение определенного интеграла к решению прикладных задач».

Знания:

- определение непрерывности и дифференцируемости функции;

- приращение функции, приращение аргумента;

- определение производной ее геометрический и механический смысл;

- таблицу производных;

- определение дифференциала.

- определение первообразной функции; определение неопределенного интеграла;

- свойства неопределенного интеграла;

- таблицу неопределенных интегралов;

- методы интегрирования;

- формулу Ньютона-Лейбница для вычисления определенных интегралов;

- методы вычисления определенных интегралов.

Умения:

- находить производные элементарных и сложных функций;

- вычислять дифференциалы функции;

- применение дифференциала к приближённым вычислениям.

- находить неопределенный интеграл различными методами;

- применять формулу Ньютона-Лейбница для вычисления определенного интеграла.

Физический и геометрический смысл производной

1. Составьте уравнение касательной к графику функции в точке с абсциссой х₀=2.

Решение:

Применение производной при исследовании функции и построении её графика

2. Постройте график функции

Решение:

Методы интегрирования

3. а) Вычислить интеграл способом непосредственного интегрирования.

Решение:

б) Вычислить интеграл подстановкой.

Решение:

в) Вычислить интеграл методом интегрирования по частям

Решение:

Определенный интеграл: Формула Ньютона-Лейбница.

4. Вычислить определенный интеграл

Решение:

Применение определенного интеграла

5. Найти площадь фигуры, ограниченной осью абсцисс и графиком функции

Решение:

Правила дифференцирования

6. а) Найдите производную функции

Решение:

б) Найдите производную сложной функции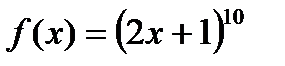

Решение: