Инверсии в перестановке. Четность перестановки. Связь с транспозициями. Четность произведения перестановок

Каждая последовательность k различных элементов с учетом порядка называется перестановкой этих элементов. Следовательно, перестановки из k элементов отличаются друг от друга только порядком входящих в них элементов. Например из первых шести чисел натурального ряда можно образовать следующие перестановки:

1,2,3,4,5,6
4,6,5,1,3,2
2,1,6,5,4,3
...
и другие.

По определению, инверсию образуют два числа в перестановке когда меньшее из них расположено правее большего. Каждой перестановке можно сопоставить число инверсий в ней, которое подсчитывается следующим образом: для каждого из чисел определяют количество стоящих правее его меньших чисел, и полученные результаты складываются.

Перестановка называется четной, если число инверсий в ней четно, и нечетной - в противном случае. В частности, рассмотренная выше перестановка нечетная, так как количество инверсий в ней равно семь.

Теорема. Любая транспозиция соседних элементов перестановки меняет четность перестановки на противоположную.

Доказательство. Пусть дана перестановка 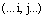, в которой мы выполним транспозицию (i j) и получим перестановку . Сразу заметим, что все пары, которые образовывали инверсию в старой перестановке, образуют инверсию и в новой, кроме возможно одной пары: (i, j). Если эта пара давала инверсию в старой перестановке, то в новой уже нет и число инверсий уменьшается на 1. Если же эта пара не образовывала инверсию в старой перестановке, то в новой образует инверсию и число инверсий увеличивается на 1. В любом случае, число инверсий изменяется на 1, а следовательно, меняется четность перестановки.

Теорема доказана.

Теорема. Любая транспозиция любых двух элементов перестановки меняет четность перестановки на противоположную.

Доказательство. Пусть выполняется транспозицию (i j) и пусть между элементами i и j находится m других элементов. Легко видеть, что такую транспозицию можно выполнить за транспозицию соседних элементов, откуда и следует теорема.

Теорема доказана.

Транспозицией называется перестановка, в которой все элементы

кроме двух остаются на месте, а два меняются местами

Лемма. Перестановка, обратная к транспозиции – транспозиция.

Лемма. Всякую перестановку можно представить в виде произведения

нескольких транспозиций. Обратную – произведения обратных

транспозиций в обратном порядке.

Инверсией перестановки называется нарушение порядка в

нижней строке перестановки. Четность перестановки положительна

(четная перестановка), если число инверсий – четное, и отрицательна

– в противном случае.

Лемма. Транспозиция – нечетная перестановка.

Лемма. Четность перестановки совпадает с четностью числа

транспозиций. Док. Индукция по числу перестановок. Следствие.

Четность произведения перестановок = произведению их четностей.