Предельные случайные последовательности

Рассмотрим вероятностное пространство 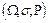в котором задана счетная последовательность случайных величин, каждая из которых является измеримой

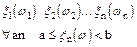
Покажем, что событие 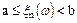измеримо, т.е. имеет вероятность наступления. Действительно событие

Каждое из этих событий в пересечении принадлежит 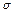- алгебре. По определению 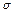- алгебры ей принадлежит и счетное перечисление этих событий, таким образом событие имеет вероятность наступления.

Пусть последовательность 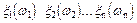имеет предел при 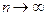, который может быть постоянной или случайной величиной. В теории вероятности этот предел понимают следующим образом: под сходимостью последовательности к пределу понимают событие А которое может задаваться следующим образом:

1.

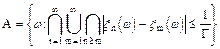
Событие А состоит из всех m, удовлетворяющих условию: для любого как угодно большого r существует такое m, что для всех n выполняется

2. А: Если предел ,то

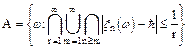
Для любого, как угодно большого r существует такое m, что для всех n выполняется

3.Если предел случайная величина, то

Показать самим, что событие А с 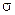- алгебре и следовательно имеет вероятность наступления

любое событие измеримо, как доказывалось ранее измеримы, и следовательно имеет вероятность наступления. Разность 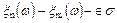-алгебре. Следовательно событие А имеет вероятность наступления.

Если предел константа, то эквиваленты 1 и 2, если случайная величина - то 1 и 3.