Свойства многомерного нормального распределения

Все одномерные плотности вероятности - это плотности вероятности одномерной нормальной случайной величины с параметрами, определяемыми координатами вектора X и главной диагональю ковариационной матрицы B. Кроме того, подвектор вектора 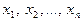из k элементов, где 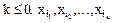также распределен нормально.

Если все коэффициенты корреляционной или ковариационной матрицы B (все ее недиагональные элементы) равны нулю, то показать самим, что компоненты случайной величины являются независимыми.

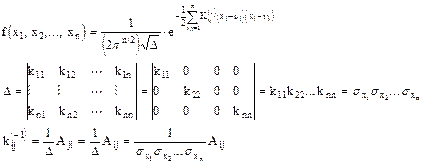
если 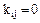,то многомерная плотность распадается на произведение одномерных, значит 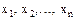независимы.

Теорема.

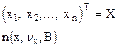
Проводим линейное преобразование Y=AX. A - квадратная невырожденная матрица, тогда вектор Y также имеет n-мерное нормальное распределение вида

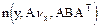
Следствие: Из доказательства теоремы вытекает, что ковариационная матрица

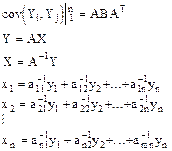
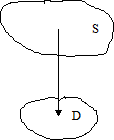
Оператор A переводит произвольную область из арифметического пространства R_n в некоторую область того же пространства.

Рассмотрим произвольную область S, принадлежащую пространству элементарных событий случайной многомерной величины X. Ей соответствует область D в пространстве элементарных событий случайного вектора Y. При этом

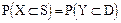
Запишем эти вероятности

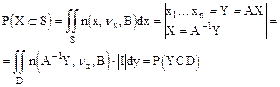
где |I| - якобиан перехода

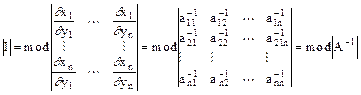
Т.к. область S и соответственно D произвольны, то плотность вероятности случайного вектора x равна

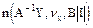
n-мерная плотность вероятности случайного вектора Y равна

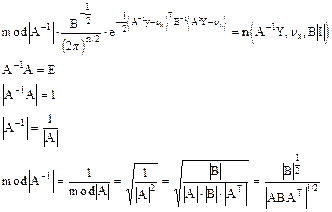
Преобразуем показатель степени e

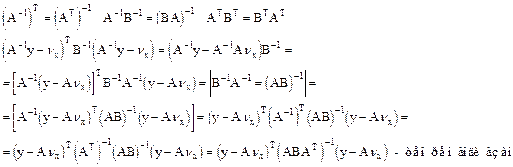
Можно показать, что если нормальное распределение имеет данный вид, то B - ее ковариационная матрица

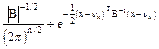
Следствие.

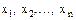- многомерный нормальный вектор. A - прямоугольная матрица 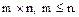Тогда Y=AX имеет нормальное распределение вида

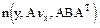
Y - m-мерный вектор.

Для определенности положим, что матрица A имеет вид

A = (A₁ A₂)

A₁ - квадратная матрица размером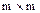

A₂ - матрица размерности

Рассмотрим матрицу размерности 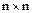. Считается, что m первых столбцов независимы.

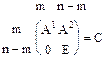
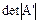равен определителю полученной квадратной матрицы и не равен нулю.

E - единственная квадратная матрица размерности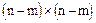

Следовательно, на основании доказанной теоремы, вектор Y имеет многомерное нормальное распределение.

Z=CX

Компоненты вектора Z имеют вид

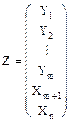
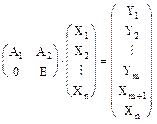
Пусть матрица А произвольная, но т.к. ее ранг равен m она содержит m линейно независимых столбцов. Путем перестановки столбцом соберем эти столбцы в первые m. И соответствующим образом пронумеруем компоненты вектора Х. Попадаем в предыдущий случай.