 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Вычисление функции Эйлера. Теорема Гаусса. Теоремы Эйлера и Ферма
|
|
Определение 14. Функцией Эйлера называется функция j(m), которая для каждого числа m Îℕ определяет количество натуральных чисел, взаимно простых с m и не превосходящих m.
Пример. Все натуральные числа, взаимно простые с m =20 и не превосходящие m: 1, 3, 7, 9, 11, 13, 17, 19. Следовательно, φ(m)=8.
Теорема 15. Пусть p - простое число, k Îℕ. Тогда φ (рk) = рk∙ 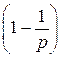 .
.
Доказательство.
Расположим числа от 1 до рk в виде таблицы:
| 1 | 2 | 3 | … | p |
| р+ 1 | р+ 2 | р+ 3 | … | p+p= 2 ∙p |
| 2∙ р+ 1 | 2∙ р+ 2 | 2∙ р+ 3 | … | 2 ∙p+p= 3 ∙p |
| … | … | … | … | … |
| (рк- 1 - 1) ∙ р+ 1 | (рк- 1 - 1) ∙ р+ 2 | (рк- 1 - 1) ∙ р+ 3 | … | (рк- 1 - 1) ∙ р+ p=рк |
Из таблицы ⇒ все столбцы, кроме последнего, взаимно просты с числом p, а значит и с числом рк . Но каждый столбец содержит рк- 1 чисел ⇒ в таблице (рк- рк- 1) чисел взаимно простых с числом рк (из рк вычтем количество элементов последнего столбца).
Таким образом, φ (рк) =pk  . Теорема доказана.
. Теорема доказана.
Теорема 16. Функция Эйлера φ(m) является мультипликативной, т.е.
1) φ(1)=1;
2) если (m,n)=1, то φ(m∙n)= φ(m)∙ φ(n).
Теорема 17. Пусть m=  - каноническое представление натурального числа m. Тогда φ (m) = m∙
- каноническое представление натурального числа m. Тогда φ (m) = m∙ 
 ∙..∙
∙..∙  .
.
Доказательство.
Так как числа р 1, р2,.., рs взаимно просты, то в силу мультипликативности функции φ (Т.16) получаем
φ (m) = φ ( ) = φ (
) = φ ( ) ∙..∙ φ (
) ∙..∙ φ ( )
) 
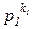 ∙
∙  ∙..∙
∙..∙ 
 = m∙
= m∙ 
 ∙..∙
∙..∙  . Теорема доказана.
. Теорема доказана.
Теорема 18 (теорема Гаусса). Пусть m Îℕ. Тогда  φ (d) =m.
φ (d) =m.
Теорема 19 (теорема Эйлера). Пусть m Îℕ, m ≠ 1, a Îℤ. Если (a,m) = 1, то aφ ( m ) ≡ 1(mod m).
Следствие 19.1 (теорема Ферма). Пусть p – простое число, a Îℤ. Если (a,p) = 1, то ap- 1 ≡ 1(mod p).
Доказательство. Так как φ (p) = p- 1, то по теореме 18 ⇒ ap- 1 ≡ 1(mod p). Следствие доказано.
Следствие 19.2. Пусть p – простое число, a Îℤ. Тогда ap ≡ a (mod p).
Доказательство. Возможны два случая:
1) Пусть a ∶ p ⇒ ap : p ⇒ (ap-a): p ⇒ ap ≡ a (mod p);
2) Пусть a: p ⇒ (a,p) = 1. По следствию 19.1, ap- 1 ≡ 1(mod p). Из свойств сравнений ⇒ ap ≡ a (mod p). Следствие доказано.
Дата публикования: 2015-11-01; Прочитано: 2080 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
