Отделение корней

Отделение корней начинается с восстановления знаков 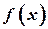в граничных точках области определения функции.

После этого, или аналитически, или графически, используя особенности функции, находят значение функции в некоторых промежуточных точках и выбирают интервалы, в которых функция имеет разные знаки на концах интервала. По условиям вышеизложенной теоремы в таких интервалах существует корень уравнения.

После этого необходимо убедиться в том, что в каждом интервале есть только один корень. В противном случае необходимо поменять интервал.

Этот метод удобен своей наглядностью, но при вычислениях вручную им не всегда можно воспользоваться, поскольку:

1. 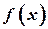может оказаться такой функцией, график которой построить очень сложно (например, ).

2. Ограниченность размеров чертежа позволяет найти корень только в некотором ограниченном промежутке.

Первый недостаток можно устранить, если удастся выписать исходное уравнение 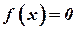в виде , при котором графики и построить значительно проще. Тогда корни уравнения находят как абсциссы точек пересечения графиков и .

Пример. Отделить корень уравнения:

Решение. Запишем это уравнение в виде 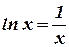. Построим графики и определим точку их пересечения (рис. 2).

Преимуществом графического метода(кроме его наглядности) является тот факт, что он часто дает возможность оценить количество корней и их знаки.