Приближенное решение нелинейных уравнений

Для достаточно сложных алгебраических и трансцендентных уравнений не всегда можно найти точное решение, поэтому очень часто приходится применять приближенные (численные) методы нахождения корней таких уравнений.

Пусть задано нелинейное уравнение (1), где функция 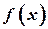определена и непрерывна на некотором (даже бесконечном) интервале . В некоторых случаях на функцию 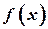можно наложить дополнительные ограничения, например, непрерывность первой и второй производной, о чем специально упоминается.

Необходимо найти корень уравнения, то есть найти те числа , которые путем подстановки их в (1) преобразовывают уравнение в верное равенство. Числа также называются нулями функции .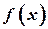

Условие существования корня уравнения (1) следует из теоремы:

Если непрерывная функция 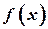принимает значения, имеющие разные знаки на концах интервала 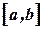, то есть 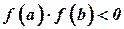, то внутри этого отрезка содержится, хотя бы, один корень уравнения 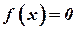. То есть, найдется хотя бы одно число такое, что . Если 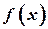является непрерывной и дифференцируемой и ее первая производная сохраняет знак внутри интервала 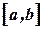, то на данном интервала можно найти только один изолированный корень уравнения.

Таким образом, при нахождении корней уравнения (1) численными методами предусматривается:

1. Функция принимает на концах интервала разные знаки;

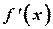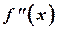2. Производные и непрерывны на интервале;

3. Производные в интервале не меняют знак.

Геометрически последнее условие означает, что предусматривается одна из четырех схем (рис. 1).

Рис. 4. 1. Геометрическая интерпретация знакопостоянства производных

Приближенное нахождение изолированных действительных корней уравнения (1) осуществляется в два этапа:

1. Находят интервалы , внутри каждого из которых содержится один и только один корень уравнения. Этот этап называется процедурой отделения корней. По сути, на этом этапе осуществляется грубое нахождение корня .

2. Грубое значение каждого корня уточняется до заданной точности одним из численных методов, в которых реализуются последовательные приближения.

Первый этап сложнее второго. Поскольку не существует достаточно эффективных методов отделения всех корней, то чаще всего используют: графический (при помощи построения и исследования графиков функций); аналитический (основанный на исследовании функции); метод последовательного перебора.