 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Теорема о необходимом и достаточном условии существовании обратной матрицы
|
|
Обратная матрица  существует (и единственна) тогда и только тогда, когда исходная матрица невырожденная
существует (и единственна) тогда и только тогда, когда исходная матрица невырожденная
Правило нахождения обратной матрицы.
Существует несколько методов вычисления обратной матрицы. Рассмотрим один из них, так называемый «метод с использованием алгебраических дополнений»
Для нахождения обратной матрицы  для матрицы А необходимо выполнить пять действий:
для матрицы А необходимо выполнить пять действий:
1.Вычислить определитель 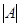 матрицы А.
матрицы А.
2. Вычислить все алгебраические дополнения для каждого элемента матрицы А.
3. Составить вспомогательную матрицу  из вычисленных дополнений.
из вычисленных дополнений.
4. Транспонировать вспомогательную матрицу  , обозначим её
, обозначим её 
5. Определить обратную матрицу  по формуле:
по формуле:  =
= 

Пример: Найти обратную матрицу для матрицы А:
А= 
Решение:
1. Вычисляем определитель матрицы А:
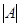 =
=  =1*2*1 - 3*2*1 + 5*1*6 - 6*2*1 - 3*5*1 + 1*2*1=1
=1*2*1 - 3*2*1 + 5*1*6 - 6*2*1 - 3*5*1 + 1*2*1=1
2. Вычисляем алгебраические дополнения к каждому элементу матрицы А:
 =4
=4  =3
=3  =-18
=-18
 =-7
=-7  =-5
=-5  =32
=32
 =3
=3 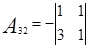 =2
=2  =-13
=-13
3. Составляем вспомогательную матрицу 
 =
= 
4. Транспонируем матрицу 
 =
= 
5 Строим обратную матрицу
 =
= 

Проверить правильность вычислений. Для этого умножим обратную матрицу на исходную:

 А=
А=  х
х  =
= 
Значит вычисления выполнены правильно.


Дата публикования: 2015-11-01; Прочитано: 383 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
