Адаптивные алгоритмы сжатия. Кодирование Хаффмена

Является практичным, однопроходным, не требующим передачи таблицы кодов. Его суть в использовании адаптивного алгоритма, т.е. алгоритма, который при каждом сопоставлении символу кода, кроме того, изменяет внутренний ход вычислений так, что в следующий раз этому же символу может быть сопоставлен другой код, т.е. происходит адаптация алгоритма к поступающим для кодирования символам. При декодировании происходит аналогичный процесс.

В начале работы алгоритма дерево кодирования содержит только один специальный символ, всегда имеющий частоту 0. Он необходим для занесения в дерево новых символов: после него код символа передается непосредственно. Обычно такой символ называют escape-символом, <ESC>. Расширенный ASCII кодируют каждый символ 8-битным числом, т.е. числом от 0 до 255. При построении дерева кодирования необходимо для возможности правильного декодирования как-то упорядочивать структуру дерева. Расположим листья дерева в порядке возрастания частот и затем в порядке возрастания стандартных кодов символов. Узлы собираются слева направо без пропусков. Левые ветви помечаются 0, а правые - 1.

Рассмотрим процесс построения кодов по адаптивному алгоритму Хаффмена для сообщения ACCBCAAABC, которое соответствует выборке 10-и значений д.с.в. из 2-го примера на построение неадаптивного кода Хаффмена:

Здесь L₁(ACCBCAAABC)=4.1 бит/сим. Если не использовать сжатия, то L₁(ACCBCAAABC)=8 бит/сим. Для рассматриваемой д.с.в. ранее были получены значения 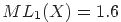бит/сим и бит/сим. С ростом длины сообщения среднее количество бит на символ сообщения при адаптивном алгоритме кодирования будет мало отличаться от значения, полученного при использовании неадаптивного метода Хаффмена или Шеннона-Фэно, т.к. алфавит символов ограничен и полный код каждого символа нужно передавать только один раз.

Теперь рассмотрим процесс декодирования сообщения 'A'0'C'100'B'1001010100101. Здесь и далее символ в апостофах означает восемь бит, представляющих собой запись двоичного числа, номера символа, в таблице ASCII+. В начале декодирования дерево Хаффмена содержит только escape-символ с частотой 0. С раскодированием каждого нового символа дерево заново перестраивается.

Выбранный способ адаптации алгоритма очень неэффективный, т.к. после обработки каждого символа нужно перестраивать все дерево кодирования. Существуют гораздо менее трудоемкие способы, при которых не нужно перестраивать все дерево, а нужно лишь незначительно изменять.

Бинарное дерево называется упорядоченным, если его узлы могут быть перечислены в порядке неубывания веса и в этом перечне узлы, имеющие общего родителя, должны находиться рядом, на одном ярусе. Причем перечисление должно идти по ярусам снизу-вверх и слева-направо в каждом ярусе.

На рис. 7.2.1 приведен пример упорядоченного дерева Хаффмена.

Рис. 7.2.1.

Если дерево кодирования упорядоченно, то при изменении веса существующего узла дерево не нужно целиком перестраивать - в нем достаточно лишь поменять местами два узла: узел, вес которого нарушил упорядоченность, и последний из следующих за ним узлов меньшего веса. После перемены мест узлов необходимо пересчитать веса всех их узлов-предков.

Например, если в дереве на рис. 7.2.1 добавить еще две буквы A, то узлы A и D должны поменяться местами (см. рис. 7.2.2).

Рис. 7.2.2.

Если добавить еще две буквы A, то необходимо будет поменять местами сначала узел A и узел, родительский для узлов D и B, а затем узел E и узел-брат E (рис.7.2.3).

Рис. 7.2.3.

Дерево нужно перестраивать только при появлении в нем нового узла-листа. Вместо полной перестройки можно добавлять новый лист справа к листу <ESC> и упорядочивать, если необходимо, полученное таким образом дерево.

Процесс работы адаптивного алгоритма Хаффмена с упорядоченным деревом можно изобразить следующей схемой: