Д) Условие прочности при изгибе

Максимальное нормальное напряжение в балке возникает в сечении, где изгибающий момент достигает наибольшей по модулю величины, то есть в опасном сечении .

Условие прочности при изгибе формулируется следующим образом: Балка будет прочной, если максимальные нормальные напряжения не превысят допускаемых напряжений

.

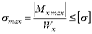Величина допускаемых напряжений назначается в зависимости от материала, из которого изготовлена балка.

Пластичные материалы обладают примерно равными пределами текучести на сжатие 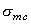и на растяжение 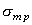равны между собой и поэтому .

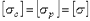Для хрупких материалов, у которых прочность при сжатии выше, чем при растяжении, допускаемые напряжения на растяжение и сжатие, как правило, не равны между собой 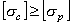и, поэтому, необходимо записывать два условия прочности

, ,

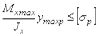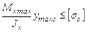где 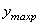и 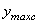- расстояния от нейтральной оси до наиболее удаленных растянутого и сжатого волокон.

18. а)поперечный изгиб. Б)Погрешности гипотез плоских сечений и о ненадавливании волокон.

А)ΣF_y=0=> Q_y=F

ΣM_y=0 => M_z=-Fx

Изгиб назыв поперечным, если в поперечном сечении возникает момент изгибающий и поперечная сила. τ=QS_x^отс/bJ_x – формула Журавского, τ_max=Q_maxS_xmax/bJ_x≤[τ] – условие прочности. Полная проверка прочности балок при поперечном изгибе заключается в определении размеров поперечного сечения по формуле Навье и дальнейшей проверки по касательным напряжениям. Т.к. наличие τ и σ в сечении относится к сложному нагружению, то оценку напряженного состояния при совместном их действии можно вычислить, используя 4 теорию прочности σ_экв4=√σ²+3τ²≤[σ].

Б)Гипотеза плоских сечений была установлена Я. Бернулли в результате экспериментов: при растяжении стержня продольные и поперечные риски, нанесенные на его поверхности до деформации, остаются прямолинейными и взаимно перпендикулярными, изменяются лишь расстояния между ними (между поперечными рисками они увеличиваются, а между продольными – уменьшаются).

В основе гипотезы плоских сечений лежит предположение, что и внутри стержня деформации имеют такой же характер, как на поверхности. Следовательно, сечения, плоские и нормальные к оси стержня до деформации, остаются плоскими и нормальными к его оси и после деформации. В этом и заключается смысл гипотезы плоских сечени