 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Метод потенціалів
|
|
При розв’язанні транспортної задачі побудований опорний план може бути досить далеким до оптимального. Тому необхідно:
по-перше, перевірити його на оптимальність,
по-друге, мати механізм його поліпшення, якщо план не є оптимальним.
Одним з методів, який дозволяє вирішити наведені завдання, є метод потенціалів.
Поставимо у відповідність кожному постачальнику A i деяку величину ui, а кожному споживачеві B j – величину vj. Ці величини називаються потенціалами постачальників та споживачів. Перевірка оптимальності базується на наступному твердженні:
Якщо план X*=(x*ij) є оптимальним, то йому відповідає така система потенціалів (u*i, v * j), для якої виконуються умови:
u*i + v*j =сij для всіх x*ij >0, (5.5)
u*i + v*j ≤сij для всіх x*ij =0, (5.6)
i =1.. m, j =1.. n.
Перша умова дозволяє відшукати систему потенціалів, а друга - перевірити план на оптимальність. Якщо план не є оптимальним (тобто, хоча б одна з умов порушується), то його поліпшення можна здійснити за рахунок однієї з тих вільних клітин, для якої має місце порушення.
Розглянемо алгоритм методу потенціалів.
1) складається система рівнянь для знаходження потенціалів. Для цього для кожної зайнятої клітини записується рівняння
ui + vj =сij. (5.7)
В отриманій системі маємо m+n– 1 рівнянь і m+n невідомих змінних (потенціалів). Тому така система має нескінчену кількість розв’язків. Нас задовольнить будь-який з них. Для цього оберемо одне зі значень одного з потенціалів довільним (вільна змінна). Як правило, для спрощення розрахунків, його обирають рівним нулю. Вибір змінної ніякого впливу на кінцевий результат не має, однак її обирають виходячи зі зручності подальших обчислень. Наприклад, в ролі вільної змінної обирають таку змінну, яка входить в найбільшу кількість рівнянь.
2) для кожної вільної клітини знаходяться величини
D ij = cij – (ui + vj). (5.8)
Якщо серед отриманих величин є від’ємні, план не є оптимальним, і його можна поліпшити.
Це здійснюється за рахунок включення у план тих клітин, (перевезень), для яких отримані від’ємні значення. Якщо всі значення оцінок D ij невід’ємні, то отриманий план є оптимальним. При цьому нульове значення величини D ij свідчить про те, що дану клітину також можна включити у план з відповідними перерахунками, однак загальна вартість перевезень при цьому не зміниться. Тобто, ми будемо мати ще один (або декілька) оптимальний план. Цей висновок важливий для практичної реалізації, коли з декількох отриманих оптимальних планів потрібно обрати той, який буде задовольняти деяким додатковим умовам.
Приклад 5.1 У двох виробників А1 і A2 є однорідний товар. У виробника А1 — 200 т, у виробника А2 — 160 т. Вказаний товар слідує відвантажити трьом споживачам Bl, B2, В3, потреба яких складає відповідно 140, 90 і 130 т. Відстані від виробника до споживача складають: від виробника А1 — 6, 4 і 2 км, від виробника A2 — 5, 3 і 2 км.
Потрібно скласти план відвантаження товару, за якого транспортні витрати були б мінімальними.
Рішення. У приведеній задачі число пунктів відправлення товару або число постачальників рівне двом, а число споживачів — трьом, тобто m = 2, а n = 3.
Очевидно, що транспортні витрати будуть якнайменшими у тому випадку, коли загальна кількість тонно-километрів буде якнайменшою.
Розташуємо всі дані в табл. 5.1.1.
Таблиця 5.1.1 - Вихідні дані
| Виробники | Наявність товару, т | Споживачі та їх потреба у товарі | ||
| В1 =140т | В2 =90т | В3 =130 т | ||
| А1 | ||||
| А2 |
Табл. 1 дозволяє нам відразу скласти першу програму. Для її отримання ми cкористуємося так званим правилом «північно-західного кута». Суть цього методу полягає в наступному: ми починаємо з відвантаження товару виробником А1 споживачу В1 тобто із заповнення клітинки А1В1, що стоїть в північно-західному кутку нашої таблиці.1. Оскільки наявність товару у виробника А1 більше потреби споживача В1 {а1>bj}, то ми віддаємо споживачу В1 всі необхідні йому 140 т, що залишилися 60 т товару — споживачу В2. Вичерпавши всі можливості виробника A1, переходимо до розподілу товару, що знаходиться у виробника A2. Оскільки попит В1 повністю задоволений, то ми переходимо до споживача В2. Йому відвантажуємо не дістаючих 30 т товару. Що залишилися в A2 130 т віддаємо споживачу В3.
Ми одержуємо першу програму або перший опорний план. При цій програмі транспортні витрати, виражені в тонно-километрах, складуть:
f1= 140x6 + 60x4 + 30x3+ 130x2= 1430 ткм.
Замітимо, що чотири клітинки виявилися заповненими. У нашій задачі число виробників m = 2, а число споживачів n = 3. Число заповнених кліток рівне, таким чином, m + n — 1 = 2 + 3 — 1 = 4.
При побудові будь-якої програми число завантажених кліток повинне бути рівне т + п— 1. Крім того, заповнені клітинки не повинні утворити циклу. Іншими словами, не повинно бути жодного прямокутника, всі вершини якого є заповненими клітинками.
Таблиця 5.1.2 – Застосування методу «північно-західного кута»
| Виробники | Наявність товару, т | Споживачі та їх потреба у товарі | ||
| В1 =140т | В2 =90т | В3 =130 т | ||
| А1 | ||||
| А2 | ||||
Останню вимогу формулюють іноді ще і так: завантажені клітинки повинні утворити викреслювану комбінацію. Це означає, що ми повинні мати нагоду викреслити всі стовпці і всі рядки, викреслюючи при цьому кожного разу не більш одну завантажену клітинку
Приклад 5.2. На складах А1, А2, А3 міститься однорідна продукція у кількостях відповідно 300, 150, 180т. Споживачі В1, В2, В3, В4 повинні отримати цю продукцію у кількостях 190, 210, 260 і 220 т відповідно.
Визначити такий варіант закріплення постачальників за споживачами, за яким загальні витрати на перевезення будуть мінімальними. Витрати на перевезення 1т продукції задаються матрицею (табл. 5.2.1). Знайти план перевезень даної транспортної задачі методом північно-західного кута, що мінімізує їх загальну вартість. Нехай транспортна задача задана наступною таблицею
Таблиця 5.2.1- Вихідні дані
| B1 190 | B2 210 | B3 260 | B4 220 | |
| A1 300 | ||||
| A2 150 | ||||
| A3 180 |
Розв’язок.
Знайдемо сумарні значення запасів вантажу та потреб у ньому.

Отже, розраховані величини не співпадають, тому дана задача є задачею відкритого типу. Щоб звести її до завдання закритого типу, уведемо фіктивного постачальника A4 з обсягом вантажу, рівного 880– 630= 250 (од). Вартості перевезень від нього до споживачів покладемо рівними нулю в результаті отримаємо наступну таблицю.
Таблиця 5.2.2 – Введення фіктивного виробника А4
| В А | B1 | B2 | B3 | B4 |
| A1 300 | ||||
| A2 150 | ||||
| A3 180 | ||||
| A4 250 |
Побудуємо опорний план, скориставшись методом мінімального елемента. Заповнення таблиці розпочинаємо з комірок з найменшим значенням вартості. В даному випадку це одна з комірок останнього рядка таблиці 5.2.2. Оберемо комірку (4.1). Оскільки при цьому запаси фіктивного споживача повністю не вичерпані, також буде заповнена ще одна комірка цього рядка, в даному випадку (4.2). Остаточно результати відображені у таблиці 3.3.
Таблиця 5.2.3– Застосування методу мінімального елемента
| В А | B1 | B2 | B3 | B4 |
| A1 300 | ||||
| A2 150 | ||||
| A3 180 | ||||
| A4 250 |
Як видно з цієї таблиці, заповненими є сім клітин, тобто, отриманий план є не виродженим. Загальна величина витрат на перевезення складає W0=3110 (г.о.)
Перевіримо отриманий план на оптимальність. Для цього скористаємось методом потенціалів.
 u 1=0, u 2= –1, u 3= 1, u 4= –6, v 1=6, v 2=6 v 3=5, v 4=4.
u 1=0, u 2= –1, u 3= 1, u 4= –6, v 1=6, v 2=6 v 3=5, v 4=4.
D11 = 3; D12 = 0; D21 = 2; D22 = 1; D24 = 3; D31 = –1; D34 = 0; D43 = 1, D44 = 2.
Отже, серед отриманих величин D ij є від’ємні, отже отриманий план можна поліпшити за рахунок клітини (3.1). Цикл перерахунку в даному випадку має вигляд (3,1) – (3,2) – (4,2) – (4,1). Новий план відображений в таблиці 5.2.4.
Таблиця 5.2.4 – Застосування методу потенціалів
| В А | B1 | B2 | B3 | B4 |
| A1 300 | ||||
| A2 150 | ||||
| A3 180 | ||||
| A4 250 |
Загальні витрати на перевезення зменшаться на 150 г.о. і становитимуть W1=2960 (г.о.).
Не відображаючи значення потенціалів цього плану, запишемо величини D ij.
D11 = 4; D12 = 1; D21 = 3; D22 = 2; D24 = 3; D32 = 1; D34 = 0; D43 = 0, D44 = 1.
Отже, отриманий в таблиці 5.2.4 план є оптимальним. Аналізуючи його, можна зробити такі висновки. Споживач B1 отримує від фіктивного споживача 40 од. вантажу. Тобто, насправді його потреби не будуть задоволені на цю ж кількість одиниць. Аналогічний висновок можна зробити стосовно споживача B2. В даному випадку його потреби не будуть задовільне ні повністю. Це є недоліком розв’язання завдання, оскільки реальні умови господарювання можуть виключати такий розв’язок. Тоді потрібно обрати інший план, який завідомо буде менш оптимальним.
Наявність нульових значень величин D ij свідчить про те, що можна побудувати ще один план, який буде рівносильний за сумарною вартістю перевезень побудованому. В даному випадку це можна зробити, включивши у план або клітину (3,4), або клітину (4,3).
В першому випадку цикл перерахунку має вигляд (3,4) – (3.3) – (1,3) – (1,4), а в другому – (4,3) – (4.10 – (3,1) – (3,3). Як видно, жоден з нових планів не включає в себе комірки другого стовпчика (тобто, інтереси споживача B2), а тому на описаний вище недолік впливу не здійснюють. Їх можна розглядати лише як альтернативу побудованому плану.
Приклад 5.3. Побудуємо за методом північно-західного кута опорний план задачі. Неважко переконатись, що дана задача є задачею закритого типу.
Перший та другий кроки наведені в таблицях 5.3.1 та 5.3.2, а опорний план – в таблиці 5.3.3.
Значення обсягів перевезень xij запишемо у нижньому правому кутку клітин таблиці. При цьому в останній стовпчик та останній рядок таблиць записуватимемо нові значення запасів та потреб.
Таблиця 5.3.1 – Перший крок методу північно-західного кута


Таблиця 5.3.2 – Другий крок методу північно-західного кута


Таблиця 5.3.3 – Опорний план, отриманий за методом північно-західного кута


Сумарні витрати на перевезення в даному випадку становлять 4∙200 + 5∙70+6∙190+…+7∙200= 4850(од)
Кількість зайнятих клітин N=7, що свідчить про те, що отриманий план є не виродженим.
Метод мінімальної вартості:
- При включенні до базису пріоритет мають змінні, яким відповідають меншим значенням cij.
- Такий підхід в загальному випадку зменшить сумарну вартість перевезень в опорному плані, а отже, він буде ближчим до оптимального.
- Серед клітин, що залишились, знову знаходиться та, якій відповідає найменша вартість перевезень, і процедура перетворення таблиці повторюється.
- Процес продовжується, доки не буде заповнена вся таблиця, тобто, не вичерпані всі запаси і не задовільнені всі потреби.
Приклад 5.4. Побудуємо за методом мінімальної вартості опорний план задачі, поданої в таблиці 5.1.1. Результати після першого та другого кроків методу а також отриманий опорний план занесемо до таблиць 5.4.1-5.4.3.
Таблиця 5.4.1 – Перший крок методу мінімальної вартості


Таблиця 5.4.2 – Другий крок методу мінімальної вартості


Таблиця 5.4.3 – Опорний план, отриманий за методом мінімальної вартості


Сумарні витрати на перевезення в даному випадку становлять 4∙90+2∙110+5∙110+…+2∙230 = 3740 (од)
Як бачимо, нами отриманий принципово інший план перевезень. І, виходячи з початкового значення W0 загальної вартості перевезень, він є кращим.
Перевіримо отриманий за методом мінімальної вартості в прикладі 5.4 опорний план на оптимальність за методом потенціалів (таблиця 5.4.3).
Перевіримо отриманий за методом мінімальної вартості опорний план на оптимальність за методом потенціалів.
Для кожної зайнятої клітини запишемо рівняння потенціалів. Отримаємо наступну систему:

В ролі вільної змінної оберемо змінну u 1=0. Тоді з першого рівняння v 1=4, а з другого v 4=2. З третього рівняння знаходимо u 2=5–4=1. Продовжуючи цей процес, знайдемо значення всіх потенціалів.
u 1=0, u 2=1, u 3= –1 v 1=4, v 2=5, v 3=3, v 4=2, v 5=3.
Далі для кожної вільної клітини розрахуємо значення оцінок D ij за формулою (5.8).
D12 = 7 – (0+5) = 2; Аналогічно D13 = 6; D15 =4; D23 = –1; D24 = 4; D32 = 4; D34 = 3; D35 = 5.
Як бачимо, серед обчислених величин є від’ємні, отже отриманий план не є оптимальним. Його можна поліпшити за рахунок включення до нього змінної x 23. Відповідно, одна зі змінних повинна вийти з опорного плану.
Включення змінної до опорного плану відбувається за таким правилом:
1. Позначимо знаком «+» клітину, яка буде відповідати новій змінній.
2. Далі побудуємо замкнений цикл, який розпочинається і закінчується у цій клітині і проходить лише через зайняті клітини. При цьому зміна маршруту в кожній новій клітині відбувається завжди під кутом 90°.
3. Побудова циклу фактично означає, яким чином зміниться обсяг вантажу, який буде перевозитись (зайняті клітини).
4. На кожному кроці включення нової клітини до циклу перерахунку будемо послідовно міняти знак з «+» на «–» і навпаки.
5. Фактично, знак «+» означає, що у відповідних клітинах збільшиться обсяг вантажу, а знак «–» – що зменшиться. Розмір вантажу, що буде переміщуватись, визначається як мінімальне значення величин xij для клітин, помічених знаком «–».
6. Такий цикл завжди існує, причому він буде єдиним. Якщо на якомусь кроці далі неможливо обрати зайняту клітину для продовження побудови циклу перерахунку, то потрібно повернутись до попереднього кроку і обрати іншу зайняту клітину.
7. Новий план знову перевіряється на оптимальність за методом потенціалів. При цьому будується нова система потенціалів.
8. Процес завершується, коли серед обчислених оцінок D ij не буде від’ємних.
Таблиця 5.4.4 – Цикл перерахунку для побудови нового плану


Початковий напрямок визначення маршруту перерахунку ролі не грає, оскільки маршрут завжди буде містити парну кількість клітин.
Таблиця 5.4.5 – Новий план перевезень


При цьому нова вартість перевезень буде становити W1 = W0 – |D23 |∙ x 21 = 3740 – 1∙110 = 3630.
 Перевіримо новий план на оптимальність. Для цього знову запишемо рівняння потенціалів.
Перевіримо новий план на оптимальність. Для цього знову запишемо рівняння потенціалів.
Розв’язок має вигляд: u 1=0, u 2=0, u 3= –1, v 1=4, v 2=6, v 3=3, v 4=2, v 5=4.
Величини D ij мають наступні значення: D12 = 1; D13 = 6; D15 =3; D21 = 1; D24 = 5; D32 = 3; D34 = 3; D35 = 4.
Оскільки серед отриманих значень D ij немає від’ємних, то побудований в таблиці 3.9 план перевезень є оптимальним.
Розподільчий метод
Сутність методу полягає в тому, що після одержання плану перевезень для кожної вільної клітинки одразу оцінюється можливість її включення до плану з метою зменшення загальної вартості перевезень.
Його перевагою є те, що не проводиться розрахунок допоміжних величин (потенціалів), а для клітинки, що включається до плану, одразу знаходиться можливий маршрут переміщення вантажу.
З іншого боку, пошук маршрутів вимагає певної кількості обчислень, що можна віднести до недоліків методу.
Алгоритм розподільчого методу має наступний вигляд:
1) Для кожної вільної клітинки знаходиться можливий маршрут переміщення вантажу.
При цьому він будується за тими ж правилами, що і для методу потенціалів: він повинен проходити лише через заповнені клітинки; в кожній клітинці повинен змінювати напрямок на 90°, і завершуватись у тій вільній клітинці, з якої він розпочинався. Початкова клітинка позначається знаком «+», а далі клітинки послідовно позначаються знаками «–» та «+».
2) Для цієї клітинки розраховується величина за вартостями тих клітинок, які увійшли до маршруту. При цьому для клітинок, помічених знаком «–», вартості також беруться зі знаком «–». Якщо значення цієї величини менше нуля, то клітинку можна включити до плану перевезень. Якщо всі побудовані оцінки додатні, то отриманий план є оптимальним.
Розглянемо застосування методу для отриманого вище початкового плану за методом мінімальної вартості.
Так, для клітини (1,2) маршрут перерахунку має наступний вигляд: (1,2): (1,2)+ – (2,2)– – (2,1)+ – (1,1)–
Тут також справа зверху біля кожної клітини маршруту вказаний знак, з яким клітина увійшла до маршруту. Тоді D12 = 7 – 6 + 5 – 4 =2
Отже, цю клітину недоцільно включати у новий план, тому що це не призведе до його поліпшення.
Аналогічно розрахуємо маршрути та величини D ij для інших незаповнених клітин. Результати розрахунків подамо у таблиці 5.4.6.
Таблиця 5.4.6 – Застосування розподільчого методу
| Клітинка | Маршрут | Значення D ij |
| (1,2) | (1,2) – (2,2) – (2,1) – (1,1) | |
| (1,3) | (1,3) – (3,3) – (3,1) – (1,1) | |
| (1,5) | (1,5) – (2,5) – (2,1) – (1,1) | |
| (2,3) | (2,3) – (3,3) – (3,1) – (2,1) | -1 |
| (2,4) | (2,4) – (1,4) – (1,1) – (2,1) | |
| (3,2) | (3,2) – (2,2) – (2,1) – (3,1) | |
| (3,4) | (3,4) – (1,4) – (1,1) – (3,1) | |
| (3,5) | (3,5) – (2,5) – (2,1) – (3,1) |
Для зручності знаки, з якими клітини увійшли до маршрутів, не відображались. Отже, в новий план потрібно включити клітину (2,3).
Звернемо увагу на те, що значення D ij вийшли такими ж, як і в методі потенціалів. Тобто, обидва методи дали однаковий результат, що свідчить про їх рівносильність.
Вибір методу, за яким здійснюється перевірка отриманого плану на оптимальність і подальша його оптимізація, рекомендується здійснювати самому користувачеві.
6. Двоїстість у лінійному програмуванні
Якщо пряма задача лінійного програмування має вигляд
 (6.1)
(6.1)
 ,
,
то двоїста задача записується так:
 (6.2)
(6.2)
за обмежень

Двоїста задача лінійного програмування утворюється з прямої задачі за такими правилами.
1. Кожному обмеженню прямої задачі відповідає змінна двоїстої задачі. Кількість невідомих двоїстої задачі дорівнює кількості обмежень прямої задачі.
2. Кожній змінній прямої задачі відповідає обмеження двоїстої задачі, причому кількість обмежень дорівнює кількості невідомих прямої задачі.
3. Якщо цільова функція прямої задачі задається на пошук найбільшого значення (max), то цільова функція двоїстої задачі — на визначення найменшого значення (min), і навпаки.
4. Коефіцієнтами при змінних в цільовій функції двоїстої задачі є вільні члени системи обмежень прямої задачі.
5. Правими частинами системи обмежень двоїстої задачі є коефіцієнти при змінних в цільовій функції прямої задачі.
6. Матриця
 ,
,
що складається з коефіцієнтів при змінних у системі обмежень прямої задачі, і матриця коефіцієнтів в системі обмежень двоїстої задачі

утворюються одна з одної транспонуванням, тобто заміною рядків стовпчиками, а стовпчиків — рядками.
Різні можливі форми прямих задач лінійного програмування та відповідні їм варіанти моделей двоїстих задач наведено у таблиці 6.1.
Таблиця 6. 1 – Можливі форми ЗЛП
| Пряма задача | Двоїста задача |
| Симетричні | |
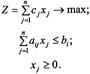
| 
|
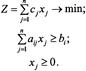
| 
|
| Несиметричні | |

| 
|

| 
|
Перша теорема двоїстості. Якщо одна з пари двоїстих задач має оптимальний план, то інша задача також має розв'язок, причому значення цільових функцій для оптимальних планів дорівнюють одне одному, тобто max Z = min F, і навпаки.
Якщо ж цільова функція однієї з пари двоїстих задач не обмежена, то друга задача взагалі не має розв'язків.
Якщо пряма задача лінійного програмування має оптимальний план X*, визначений симплекс-методом, то оптимальний план двоїстої задачі Y* визначається зі співвідношення:
 (6.3)
(6.3)
де  — вектор-рядок, що складається з коефіцієнтів цільової функції прямої задачі при змінних, які є базисними в оптимальному плані;
— вектор-рядок, що складається з коефіцієнтів цільової функції прямої задачі при змінних, які є базисними в оптимальному плані;
 — матриця, обернена до матриці D складеної з базисних векторів оптимального плану, компоненти яких узято з початкового опорного плану задачі. Обернена матриця
— матриця, обернена до матриці D складеної з базисних векторів оптимального плану, компоненти яких узято з початкового опорного плану задачі. Обернена матриця  завжди міститься в останній симплекс-таблиці в тих стовпчиках, де в першій таблиці містилася одинична матриця.
завжди міститься в останній симплекс-таблиці в тих стовпчиках, де в першій таблиці містилася одинична матриця.
За допомогою зазначеного співвідношення під час визначення оптимального плану однієї з пари двоїстих задач лінійного програмування знаходять розв'язок іншої задачі.
Друга теорема двоїстості. Якщо в результаті підстановки оптимального плану прямої задачі в систему обмежень цієї задачі i -те обмеження виконується як строга нерівність, то відповідний i -й компонент оптимального плану двоїстої задачі дорівнює нулю. Якщо i -й компонент оптимального плану двоїстої задачі додатний, то відповідне i -те обмеження прямої задачі виконується для оптимального плану як рівняння.
Третя теорема двоїстості. Двоїста оцінка характеризує приріст цільової функції, який зумовлений малими змінами вільного члена відповідного обмеження.
Економічний зміст третьої теореми двоїстості полягає в тому, що відповідна додатна оцінка показує зростання значення цільової функції прямої задачі, якщо запас відповідного дефіцитного ресурсу збільшується на одну одиницю.
Приклад 6.1. До наведеної далі задачі лінійного програмування записати двоїсту задачу. Розв'язати одну з них симплекс-методом та визначити оптимальний план іншої задачі.

Розв'язування. Перш ніж записати двоїсту задачу, необхідно пряму задачу звести до відповідного вигляду. Оскільки цільова функція Z максимізується і в системі обмежень є нерівності, то вони повинні мати знак « ». Тому перше обмеження моделі помножимо на (-1). При цьому знак нерівності зміниться на протилежний. Отримаємо:
». Тому перше обмеження моделі помножимо на (-1). При цьому знак нерівності зміниться на протилежний. Отримаємо:

Тепер за відповідними правилами складемо двоїсту задачу:
 .
.
Оскільки записані задачі симетричні, будь-яку з них можна розв'язати симплекс-методом. Наприклад, визначимо спочатку оптимальний план прямої задачі. Для цього застосуємо алгоритм симплекс-методу.

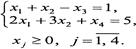
2. Векторна форма запису системи обмежень має вигляд


У системі векторів для утворення початкового одиничного базису відсутній вектор 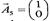 . Тому використаємо штучну змінну в першому обмеженні.
. Тому використаємо штучну змінну в першому обмеженні.
3. Розширена задача лінійного програмування буде така:


У цій задачі х4 та х5 - базисні змінні, а х1, х2, х3 — вільні. Нехай х1 = х2 = х3 = 0, тоді х4 = 5; х5 = 1.
Перший опорний план задачі: х0 = (0;0;0;5;1),Zо = -М.
4. Подальше розв'язування прямої задачі подано у вигляді симплекс-таблиці:
Таблиця 6.2 –Симплекс-таблиця розв’язку прямої задачі
| Базис | Сбаз | План | -5 | М | 
| |||
| х1 | x2 | х3 | х4 | х5 | ||||
 х5 х5
| -М | 
| -1 | |||||
| х4 | 5/3 | |||||||
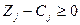
| -2 | |||||||
| -M | -М | -М | M | |||||
| х2 | -1 | - | ||||||
 х4 х4
| -1 | 
| -3 | 2/3 | ||||
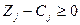
| -2 | 2 + М | ||||||
| x2 | 5/3 | 2/3 | 1/3 | |||||
| x3 | 2/3 | -1/3 | 1/3 | -1 | ||||

| 10/3 | 19/3 | 2/3 | 0 + M |
З останньої симплекс-таблиці бачимо, що оптимальний план прямої задачі
X* = (0; 5/3; 2/3; 0), Z max= 10/3.
Згідно зі співвідношенням двоїстості за першою теоремою можна записати, що оптимальний план двоїстої задачі існує і min F = max Z = 10/3, С6аз = (2; 0) та міститься в стовпчику «Сбаз» останньої симплекс-таблиці;

він також міститься в останній симплекс-таблиці у стовпчиках змінних «Х5» та «Х4», які утворювали початковий базис. Отже,
 ,
,
min F = -1 -0 + 5-2/3 = 10/3.
Застосовуючи до розв'язування прямої задачі симплекс-метод, ми знайшли її оптимальний план, а потім визначили оптимальний розв'язок двоїстої задачі за допомогою співвідношень першої теореми двоїстості.
Задача 6.2. До наведеної далі задачі лінійного програмування записати двоїсту задачу. Розв'язавши двоїсту задачу графічно, визначити оптимальний план прямої задачі.

Розв'язування. За відповідними правилами побудуємо двоїсту задачу:

 .
.
Зауважимо, що задачі несиметричні, і тому змінна y1, що відповідає рівнянню в системі обмежень прямої задачі, може мати будь-який знак, а змінна y2 — лише невід'ємна.
Двоїста задача має дві змінні, а отже, її можна розв'язати графічно (рис. 6.1).

Рисунок 6.1 – Графічна інтерпретація двоїстої задачі
Найбільшого значення цільова функція двоїстої задачі F досягає в точці В многокутника АВСD. її координати:

тобто Y* = (-2/3; 4/3); max F= 1 • (-2/3) + 4*4/3 = 14/3.
Оптимальний план прямої задачі визначимо за допомогою співвідношень другої теореми двоїстості.
Підставимо Y* у систему обмежень двоїстої задачі і з'ясуємо, як виконуються обмеження цієї задачі:

Оскільки перше обмеження для оптимального плану двоїстої задачі виконується як строга нерівність, доходимо висновку, що перша змінна прямої задачі дорівнюватиме нулю х1=0 (перша частина другої теореми двоїстості).
Тепер проаналізуємо оптимальний план двоїстої задачі. Оскільки друга компонента плану у2 = 4/3 додатна, доходимо висновку, що друге обмеження прямої задачі для X* виконуватиметься як строге рівняння (друга частина другої теореми двоїстості).
Об'єднуючи здобуту інформацію, можна записати систему обмежень прямої задачі як систему двох рівнянь, в якій х1 = 0, та визначити решту змінних:

тобто Х* = (0; 5/3; 2/3), min Z = 1 • 0 + 2 • 5/3 +2 • 2/3 = 14/3.
Умова min Z = max F = 14/3 виконується, і тому X* = (0; 5/3; 2/3); Y* = (—2/3; 4/3) є оптимальними планами відповідно прямої та двоїстої задач.
7. Цілочислове програмування
Економіко-математичні моделі у яких одна або кілька змінних мають набувати цілих значень, тобто коли така вимога випливає з особливостей технології виробництва називаються цілочисловим програмуванням. Для знаходження оптимальних планів задач цілочислового програмування застосовують дві основні групи методів (рис.7.1):
1) методи відтинання:
а) методи розв'язування повністю цілочислових задач (дробовий алгоритм Гоморі);
б) методи розв'язування частково цілочислових задач (другий алгоритм Гоморі, або змішаний алгоритм цілочислового програмування).
2) комбінаторні методи: метод віток і меж.

Рисунок 7.1. – Методи цілочислового програмування
Основою методів відтинання є ідея поступового «звуження» області допустимих розв'язків розглядуваної задачі. Пошук цілочислового оптимуму починається з розв'язування задачі з так званими послабленими обмеженнями, тобто без урахування вимог цілочисловості змінних. Далі введенням у модель спеціальних додаткових обмежень, що враховують цілочисловість змінних, многокутник допустимих розв'язків послабленої задачі поступово зменшуємо доти, доки змінні оптимального розв'язку не набудуть цілочислових значень.
Комбінаторні методи цілочислової оптимізації базуються на повному переборі всіх допустимих цілочислових розв'язків, тобто вони реалізують процедуру цілеспрямованого перебору, під час якої розглядається лише частина розв'язків (досить невелика), а решта враховується одним зі спеціальних методів.
За методом віток і меж починають з розв'язування послабленої задачі шляхом розбиття початкової задачі на дві підзадачі виключенням областей, що не мають цілочислових розв'язків, і дослідженням кожної окремої частини многокутника допустимих розв'язків.
Загальна задача цілочислового програмування записується так:
 , (7.1)
, (7.1)
за обмежень  (7.2)
(7.2)
 (7.3)
(7.3)
 (7.4)
(7.4)
Для її розв'язування застосовують ітеративний метод Гоморі:
1. Знаходять розв'язок послабленої, тобто задачі без вимог цілочисловості змінних - (7.1)-(7.3). Якщо серед елементів умовно-оптимального плану немає дробових чисел, то цей план є оптимальним планом задачі цілочислового програмування (7.1)-(7.4).
2. Коли в умовно-оптимальному плані є дробові значення, то вибирається змінна, яка має найбільшу дробову частину. На базі цієї змінної (елементів відповідного рядка останньої симплексної таблиці, в якому вона міститься) будується додаткове обмеження Гоморі:
 (7..5)
(7..5)
де символ { aij } позначає дробову частину числа.
Для визначення дробової частини будь-якого числа від цього числа віднімають цілу його частину — найбільше ціле число, що не перевищує даного. Цілу частину числа позначають символом [ ]. Наприклад, [1,3] = 1; [-1,3] = -2.
3. Додаткове обмеження після зведення його до канонічного вигляду і введення базисного елемента приєднується до останньої симплексної таблиці, яка містить умовно-оптимальний план. Здобуту розширену задачу розв'язують, а далі перевіряють її розв'язок на цілочисловість. Якщо він не цілочисловий, то процедуру повторюють, повертаючись до п. 2. Так діють доти, доки не буде знайдено цілочислового розв'язку або доведено, що задача не має допустимих розв'язків у множині цілих чисел.
Метод «віток і меж»
Нехай потрібно знайти xj — цілочислову змінну, значення якої xj* в оптимальному плані послабленої задачі є дробовим. Тоді можна стверджувати, що в інтервалі ([xj*], [хj*] + 1) цілих значень немає. Отже, допустиме ціле значення хj має задовольняти одну з нерівностей:
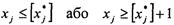 .
.
Приписавши кожну з цих умов до задачі з послабленими обмеженнями, дістанемо дві не пов'язані між собою задачі. Тобто початкову задачу цілочислового програмування (7.1)—(74) розіб'ємо на дві задачі з урахуванням умов цілочисловості змінних, значення яких в оптимальному плані послабленої задачі є дробовими. Це означає, що симплекс-методом розв'язуватимемо дві такі задачі:
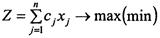 (7.6)
за умов (7.6)
за умов
| |
 (7.7) (7.7)
 (7.8) (7.8)
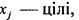 (7.9) (7.9)
 (7.10) (7.10)
 (7.11) (7.11)
|  (7.12) (7.12)
 (7.13) (7.13)
 (7.14) (7.14)
 (7.15)
де xj* - компонент розв'язку задачі (7.1)—(7.4). (7.15)
де xj* - компонент розв'язку задачі (7.1)—(7.4).
|
Далі симплекс-методом розв'язуємо послаблені задачі (7.7)— (7.10) і (7.12)—(7.15), тобто з відкиданням обмежень (7.9) і (7.14). Якщо знайдені оптимальні плани задовольняють умови цілочисловості, то ці плани є розв'язками задачі (7.1)—(7.4). Інакше пошук розв'язку задачі триває. Для подальшого розгалуження беремо задачу з найбільшим значенням цільової функції, якщо йдеться про максимізацію, і навпаки — з найменшим значенням цільової функції в разі її мінімізації. Подальше розгалуження виконується доти, доки не буде встановлено неможливість поліпшення розв'язку. Здобутий план — оптимальний.
Приклади цілочислових економічних задач
Задача 7.1. Задача лінійного розкрою. У цеху розрізують прути завдовжки 6 м на заготівки 1,4; 2 і 2,5 м. Усього в цеху мають 200 прутів. Потрібно дістати не менше як 40, 60 і 50 заготівок завдовжки відповідно 1,4; 2 і 2,5 м. Побудувати загальну і числову модель лінійного розкрою. За критерій оптимізації є сенс узяти мінімум відходів.
Розв'язування. Нехай  — вид заготівки. Кожний прут можна розрізати різними
— вид заготівки. Кожний прут можна розрізати різними  способами.
способами.
Скористаємося такими позначеннями:
аij — вихід заготовок i-го виду в разі розрізування прута j-м способом;
сj -— відходи в разі розрізування прута j-м способом;
А — кількість наявних прутів;
Ві, Di — відповідно нижня і верхня межі потреби в i-й заготівці;
xj — кількість прутів, які розрізані за j-м варіантом.
Запишемо загальну економіко-математичну модель лінійного розкрою.
Критерій оптимальності: 
за умов 

Побудуємо числову економіко-математичну модель розрізування прутів, розглянувши можливі варіанти такого розрізування:
| Довжина заготівки, м | Варіанти розрізування прутів | ||||||
| x1 | x2 | х3 | x4 | x5 | x6 | x7 | |
| 1,4 | - | — | |||||
| — | — | — | |||||
| 2,5 | — | — | — | ||||
| Довжина відходів, м | 0,4 | 0,1 | 0,6 | 1,2 | 0,7 |
Бажано, щоб у множину ввійшли всі можливі варіанти, навіть такі, які на перший погляд здаються неефективними, наприклад х6. Запишемо числову економіко-математичну модель розрізування прутів:

за умов: а) щодо кількості заготівок завдовжки
1,4 м: 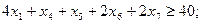
2 м: 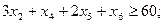 2,5 м:
2,5 м: 
б) щодо кількості наявних прутів:

в) щодо невід'ємності змінних:
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
, 
г) щодо цілочисловості змінних: х1, х2, х3, х4, х5, х6, х7 — цілі числа. Пропонуємо розв'язати цю задачу одним із методів цілочислового програмування.
Задача 7.2. Задача комівояжера. В економічному регіоні розміщено 6 пунктів (міст). Комівояжер, який виїжджає з міста 1, має побувати в кожному місті один раз і повернутися до вихідного пункту. Знайти найкоротший маршрут, якщо відстані між містами відомі (рис. 7.2). Записати загальну і числову економіко-математичну модель.

Рисунок 7.2. – Відстані між містами
Розв'язування. Нехай маємо п пунктів, де має побувати комівояжер.
Позначимо:
 .
.
Отже, хij — бульові (цілочислові) змінні. Цільовою функцією цієї задачі є мінімізація всього маршруту комівояжера:
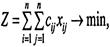
де cij — відстань між містами i та j.
Обмеження щодо одноразового в'їзду в кожне місто:

Обмеження щодо одноразового виїзду з кожного міста:

Ці обмеження не повністю описують допустимі маршрути і не виключають можливості розриву маршруту. Щоб усунути цей недолік, введемо додаткові змінні  , які набувають невід'ємних цілих значень. Запишемо обмеження, які виключають можливість існування підмаршрутів:
, які набувають невід'ємних цілих значень. Запишемо обмеження, які виключають можливість існування підмаршрутів:

де  — порядковий номер міста за маршрутом прямування комівояжера.
— порядковий номер міста за маршрутом прямування комівояжера.
Запишемо числову економіко-математичну модель комівояжера за розглядуваних умов.
Критерій оптимальності:

а) обмеження щодо одноразового в'їзду в кожне місто:
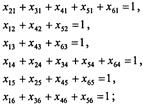
б) обмеження щодо одноразового виїзду з кожного міста:

в) обмеження щодо виключення підмаршрутів:


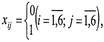
де  — цілі числа (i = 2,6; j = 2,6;
— цілі числа (i = 2,6; j = 2,6;  ).
).
Такі задачі розв'язуються спеціальними методами [1; 10].
Зауважимо, що аналогічні задачі нерідко постають на практиці, наприклад, у дрібному бізнесі.
Задача 7.3. Фермер планує виробляти три види продукції — озиму пшеницю, цукрові буряки та молоко. Сумарні витрати складаються з двох частин: постійних — kj, які не залежать від обсягу виробництва, і поточних cj на виробництво одиниці продукції, де j — номер продукції. Відповідні дані наведено в таблиці:
| Показник | Вид продукції | ||
| Озима пшениця, т | Цукровий буряк, т | Молоко, т | |
| Постійні витрати, тис. грн. | |||
| Поточні витрати на одиницю продукції, грн. | |||
| Норма витрат ріллі, га | 0,2 | 0,02 | 0,25 |
| Ціна одиниці продукції, грн. |
Визначити оптимальний план виробництва продукції кожного виду, якщо з цією метою використовується 100 га ріллі.
Розв'язування. Нехай xj — обсяг виробництва j-го виду продукції, j=1,3. Функція сумарних витрат на виробництво j-ї продукції набуває вигляду:

Як цільову функцію беремо максимізацію валового прибутку:

де уj — ціна одиниці j-ї продукції.
Обмеження щодо ріллі: 
де аj - — норма витрат ріллі на одиницю j-ї продукції; А — ресурс ріллі.
Цільова функція цієї задачі не є лінійною, оскільки має розрив у початку координат. Отже, ця задача не може бути розв'язана симплексним методом.
Щоб розв'язати цю задачу, скористаємося штучним прийомом. Введемо бульові змінні такою умовою:

її можна записати у вигляді лінійної нерівності

де М — досить велике число, за якого умова  виконується для всіх допустимих обсягів виробництва продукції.
виконується для всіх допустимих обсягів виробництва продукції.
У результаті маємо таку економіко-математичну модель:
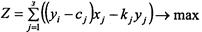
за умов 


Запишемо числову економіко-математичну модель. Очевидно, що максимум пшениці становить 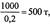 , цукрових буряків —
, цукрових буряків —  молока —
молока —  . Отже, М може дорівнювати 5000. Звідси маємо:
. Отже, М може дорівнювати 5000. Звідси маємо:

за умов
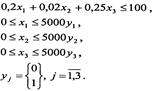
Аналогічні задачі застосовують для оцінки ефективності нового бізнесу.
Задача 7.4. Задача планування виробничої лінії. Оптимізувати режим функціонування виробничої лінії, яка охоплює 11 операцій з виготовлення двох виробів. Лінію обладнано одним багатоопераційним верстатом. Послідовність і тривалість (у хвилинах) виконання операцій відбиває рис. 7.3.

Рисунок 7.3. - Послідовність і тривалість (у хвилинах) виконання операцій
Установлено термін виготовлення кожного з виробів А та В як проміжок часу від деякого початкового моменту. Нехай це буде відповідно 120 і 150 хв. Передбачається, що в кожний момент часу на верстаті може виконуватися одна операція.
Визначити оптимальний термін початку кожної операції.
Розв'язування. Розглянемо спочатку задачу в загальному вигляді, скориставшись позначеннями:
 — час виконання j-ї операції (j = 1,n);
— час виконання j-ї операції (j = 1,n);
 — момент часу (термін) для j-го виробу, до якого необхідно завершити операцію j;
— момент часу (термін) для j-го виробу, до якого необхідно завершити операцію j;
 — час (термін) початку j-ї операції;
— час (термін) початку j-ї операції;
t — сумарний час виконання всіх операцій.
Економіко-математична модель містить три типи обмежень:
1. Послідовність виконання і-ї операції записується для всіх пар операцій 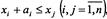 якщо i-та операція передує в часі j-й операції.
якщо i-та операція передує в часі j-й операції.
2. Обмеження не розгалуженості виробничого процесу для операцій i та j, які не виконуються одночасно  , має вигляд:
, має вигляд:
або  , якщо операція j передує в часі операції i;
, якщо операція j передує в часі операції i;
або  , якщо операція i передує в часі операції j.
, якщо операція i передує в часі операції j.
Зауважимо, що логічні обмеження виду «або-або» не можуть входити до економіко-математичної моделі задачі лінійного програмування, оскільки породжують не опуклу множину допустимих розв'язків. Тому необхідно ввести допоміжні змінні, які дозволяють записати наведені щойно логічні умови у вигляді лінійних обмежень. Це такі бульові змінні:

Увівши змінні  запишемо шукані обмеження:
запишемо шукані обмеження:

де М— досить велике число.
3. Обмеження щодо термінів виготовлення кожного виробу:
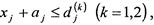
де j — остання операція для k-то виробу.
4. Усі операції мають бути виконанні до моменту часу t:

Критерій оптимальності: 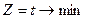 тобто ставиться задача, щоб обидва вироби були виготовлені за мінімальний час.
тобто ставиться задача, щоб обидва вироби були виготовлені за мінімальний час.
Запишемо числову економіко-математичну модель: 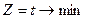 , за наведених далі умов.
, за наведених далі умов.
1. Послідовність виконання операцій:

2. Обмеження щодо не розгалуженості виробничого процесу:


3. Обмеження щодо термінів виготовлення виробів: 
4. Усі операції мають бути виконані до моменту часу

5. Обмеження на змінні: 
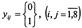
Отже, маємо частково цілочислову задачу з бульовими змінними.
Задача 7.5 Задача оптимального призначення. Розподілити чотирьох робітників за чотирма видами устаткування так, щоб їх загальна продуктивність праці була максимальною. Дані стосовно продуктивності праці кожного робітника на устаткуванні кожного виду наведено в таблиці:
| Робітник | Продуктивність праці, грн./год, на устаткуванні | |||
Розв'язування. Дану задачу можна розглядати як транспортну, в якій робітники ототожнюються з постачальниками вантажів, а види устаткування — зі споживачами цих вантажів. Обсяги пропозиції та попиту в кожному випадку дорівнюють одиниці. Отже, змінні будуть бульовими:
 .
.
Якщо cij — продуктивність праці і-го робітника на j-му устаткуванні, то економіко-математичну модель про призначення у загальному вигляді можна записати так:

за умов

Числова модель набирає вигляду:

за умов

З огляду на особливу структуру цієї задачі, зокрема її «транспортний» характер та рівність правих частин обмежень, для розв'язування можна застосувати ефективніший алгоритм, ніж для звичайної задачі цілочислового програмування з бульовими змінними.
8. Нелінійні оптимізаційні моделі економічних систем
Розв'язуючи задачі оптимального управління (планування), доводиться враховувати нелінійний характер взаємозв'язків між економічними показниками. У загальному вигляді нелінійна економіко-математична модель має вигляд:
 (8.1)
(8.1)
за умов
 , (8.2)
, (8.2)
де  і
і  —нелінійні функції.
—нелінійні функції.
Задачу нелінійного програмування намагаються звести до лінійного вигляду. Проте в такому разі можливі значні похибки. Нехай, наприклад, собівартість продукції у визначено як функцію  , де х — обсяги виробництва. Ввівши заміну
, де х — обсяги виробництва. Ввівши заміну  , дістанемо лінійну залежність
, дістанемо лінійну залежність  . За такої заміни похибки немає. А коли
. За такої заміни похибки немає. А коли  , то заміна цієї залежності деякою лінійною функцією
, то заміна цієї залежності деякою лінійною функцією  призводить до значних похибок, що ілюструє рис. 8.1.
призводить до значних похибок, що ілюструє рис. 8.1.

Рисунок8.1 - Графічне зображення похибки двох функцій
У точках х1 і х3, значення собівартості для обох розглядуваних функцій однакові, але в усіх інших точках ці значення відрізняються, причому в точці х2 значною мірою:
Дата публикования: 2015-10-09; Прочитано: 3557 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
