Задание № 2. 1. На основе структурных группировок из задания 1 построить вариационные частотные и кумулятивные ряды распределения (по каждому признаку)

1. На основе структурных группировок из задания 1 построить вариационные частотные и кумулятивные ряды распределения (по каждому признаку), оформить в таблицы, изобразить графически.

2. Проанализировать вариационные ряды распределения, вычислив для каждого из них:

· среднее арифметическое значение признака;

· медиану, квартили и моду;

· среднее квадратическое отклонение;

· коэффициент вариации.

3. Проверить теорему о разложении дисперсии, используя данные о аналитической группировки.

4. Изобразить корреляционное поле. Построить уравнение регрессии. Определить тесноту связи между признаками, используя дисперсионный и корреляционный анализ.

5. Сделать выводы.

Ряд распределения – это числовой ряд, который представляет собой упорядоченное распределение единиц статистической совокупности. Он характеризует состав (структуру) изучаемого явления.

Объем совокупности: N = 30.

Таблица 2.1.

Вариационный частотный и кумулятивный ряд распределения по среднегодовой численности, занятых в экономике, млн. чел.

Группы	xi	Кол-во, fi	xi * fi	Накопленная частота, S	(x - xср)2*f
0.03 - 0.51	0.27		3.24		3.98
0.51 - 0.99	0.75				0.0737
0.99 - 1.47	1.23		7.38		0.88
1.47 - 1.95	1.71		1.71		0.75
1.95 - 2.43	2.19		4.38		3.61
2.43 - 2.91	2.67		2.67		3.33
Итого			25.38		12.63

Гистограмма – графическое изображение интервального ряда распределения. При ее построении на оси абсцисс откладывают интервалы ряда. Над осью абсцисс строятся прямоугольники, основанием которых является интервал, а высота – соответствующая этому интервалу частота.

Кумулята – ломаная линия, изображающая ряд накопленных частот. Накопленные частоты наносятся в системе координат в виде ординат для границ интервалов; соединяя нанесенные точки отрезками прямых, получаем кумуляту. Кумуляту называют также полигоном накопленных частот.

Рис.1. Гистограмма вариационного ряда по среднегодовой численности занятых в экономике, млн.чел.

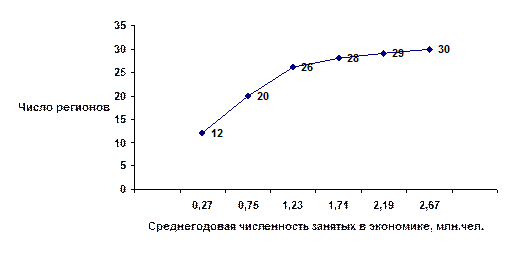
Рис. 2. Кумулята вариационного ряда по среднегодовой численности занятых в экономике, млн.чел..

Рис. 3. Полигон вариационного ряда по среднегодовой численности занятых в экономике, млн.чел.

Таблица 2.2.

Вариационный частотный и кумулятивный ряд распределения по числу дорожно-транспортных происшествий на 100 тыс. населения

Группы	xi	Кол-во, fi	xi * fi	Накопленная частота, S	(x - xср)2*f
59.2 - 105	82.1		328.4		17237.94
105 - 150.8	127.9		1534.8		4726.68
150.8 - 196.6	173.7		1910.7		7409.33
196.6 - 242.4	219.5		658.5		15445.62
Итого			4432.4		44819.57

Рис. 4. Гистограмма вариационного ряда по числу дорожно-транспортных происшествий.

Рис. 5. Кумулята вариационного ряда по числу дорожно-транспортных происшествий.

Рис. 6. Полигон вариационного ряда по числу дорожно-транспортных происшествий.

Признак № 1: Среднегодовая численность занятых в экономике, млн. чел.

Таблица 2.3.

Вычисление среднего арифметического значения признака, среднего квадратического отклонения для вариационного ряда среднегодовой численности, занятых в экономике

Группы	xi	Кол-во, fi	xi * fi	Накопленная частота, S	(x - xср)2*f
0.03 - 0.51	0.27		3.24		3.98
0.51 - 0.99	0.75				0.0737
0.99 - 1.47	1.23		7.38		0.88
1.47 - 1.95	1.71		1.71		0.75
1.95 - 2.43	2.19		4.38		3.61
2.43 - 2.91	2.67		2.67		3.33
Итого			25.38		12.63

Мода

Мода - наиболее часто встречающееся значение признака у единиц данной совокупности.

где x₀ – начало модального интервала; h – величина интервала; f₂ –частота, соответствующая модальному интервалу; f₁ – предмодальная частота; f₃ – послемодальная частота.

Выбираем в качестве начала интервала 0.03, так как именно на этот интервал приходится наибольшее количество.

Наиболее часто встречающееся значение ряда – 0.39

Медиана

Медиана делит выборку на две части: половина вариант меньше медианы, половина — больше.

В интервальном ряду распределения сразу можно указать только интервал, в котором будут находиться мода или медиана. Медиана соответствует варианту, стоящему в середине ранжированного ряда. Медианным является интервал 0.03 - 0.51, т.к. в этом интервале накопленная частота S, больше медианного номера (медианным называется первый интервал, накопленная частота S которого превышает половину общей суммы частот).

Таким образом, 50% единиц совокупности будут меньше по величине 0.69

Квартили.

Квартили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 25% единиц совокупности будут меньше по величине Q₁; 25% будут заключены между Q₁ и Q₂; 25% - между Q₂ и Q₃; остальные 25% превосходят Q₃.

Таким образом, 25% единиц совокупности будут меньше по величине 0.33

Q₂ совпадает с медианой, Q₂ = 0.69

Остальные 25% превосходят значение 1.19.

Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего).

Среднее квадратическое отклонение (средняя ошибка выборки).

Каждое значение ряда отличается от среднего значения 0.85 в среднем на 0.65

Коэффициент вариации - мера относительного разброса значений совокупности: показывает, какую долю среднего значения этой величины составляет ее средний разброс.

Поскольку v>70%, то совокупность приближается к грани неоднородности, а вариация сильная.

Признак № 2 – число дорожно-транспортных происшествий на 100 тыс. населения

Таблица 2.4.

Вычисление среднего арифметического значения признака для вариационного ряда распределения числа дорожно-транспортных происшествий на 100 тыс. населения

Группы	xi	Кол-во, fi	xi * fi	Накопленная частота, S	(x - xср)2*f
59.2 - 105	82.1		328.4		17237.94
105 - 150.8	127.9		1534.8		4726.68
150.8 - 196.6	173.7		1910.7		7409.33
196.6 - 242.4	219.5		658.5		15445.62
Итого			4432.4		44819.57

Мода

Мода - наиболее часто встречающееся значение признака у единиц данной совокупности.

где x₀ – начало модального интервала; h – величина интервала; f₂ –частота, соответствующая модальному интервалу; f₁ – предмодальная частота; f₃ – послемодальная частота.

Выбираем в качестве начала интервала 105, так как именно на этот интервал приходится наибольшее количество.

Наиболее часто встречающееся значение ряда – 145.71

Медиана

Медиана делит выборку на две части: половина вариант меньше медианы, половина — больше.

В интервальном ряду распределения сразу можно указать только интервал, в котором будут находиться мода или медиана. Медиана соответствует варианту, стоящему в середине ранжированного ряда. Медианным является интервал 105 - 150.8, т.к. в этом интервале накопленная частота S, больше медианного номера (медианным называется первый интервал, накопленная частота S которого превышает половину общей суммы частот).

Таким образом, 50% единиц совокупности будут меньше по величине 146.98

Квартили.

Квартили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 25% единиц совокупности будут меньше по величине Q₁; 25% будут заключены между Q₁ и Q₂; 25% - между Q₂ и Q₃; остальные 25% превосходят Q₃.

Таким образом, 25% единиц совокупности будут меньше по величине 118.36

Q₂ совпадает с медианой, Q₂ = 146.98

Остальные 25% превосходят значение 177.86.

Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего).

Среднее квадратическое отклонение (средняя ошибка выборки).

Каждое значение ряда отличается от среднего значения 147.75 в среднем на 38.65

Относительные показатели вариации.

К относительным показателям вариации относят: коэффициент осцилляции, линейный коэффициент вариации, относительное линейное отклонение.

Коэффициент вариации - мера относительного разброса значений совокупности: показывает, какую долю среднего значения этой величины составляет ее средний разброс.

Поскольку v ≤ 30%, то совокупность однородна, а вариация слабая. Полученным результатам можно доверять.

3.

По аналитической группировке измеряют связь при помощи эмпирического корреляционного отношения. Оно основано на правиле разложения дисперсии: общая дисперсия равна сумме внутригрупповой и межгрупповой дисперсий.

1. Находим средние значения каждой группы.

Общее средние значение для всей совокупности:

2. Дисперсия внутри группы при относительном постоянстве признака-фактора возникает за счет других факторов (не связанных с изучением). Эта дисперсия называется остаточной:

Расчет для группы: 0.03 - 0.51 (1,2,3,4,5,6,7,8,9,10,11,12)

Таблица 2.5

Расчетная таблица

yj	(yj - yср)2	Результат
59.2	(59.2 - 158.94)2	9948.4
242.4	(242.4 - 158.94)2	6965.29
	(218.0 - 158.94)2	3487.89
	(196.0 - 158.94)2	1373.32
158.6	(158.6 - 158.94)2	0.12
145.2	(145.2 - 158.94)2	188.83
152.7	(152.7 - 158.94)2	38.96

Продолжение таблицы 2.5

149.9	(149.9 - 158.94)2	81.75
125.8	(125.8 - 158.94)2	1098.37
88.9	(88.9 - 158.94)2	4905.84
189.5	(189.5 - 158.94)2	933.81
181.1	(181.1 - 158.94)2	490.99
Итого		29513.57

Определим групповую (частную) дисперсию для 1-ой группы:

Расчет для группы: 0.51 - 1 (13,14,15,16,17,18,19,20)

Таблица 2.6

Расчетная таблица

yj	(yj - yср)2	Результат
143.5	(143.5 - 154.33)2	117.18
123.9	(123.9 - 154.33)2	925.68
173.7	(173.7 - 154.33)2	375.39
124.6	(124.6 - 154.33)2	883.58
95.8	(95.8 - 154.33)2	3425.18
230.6	(230.6 - 154.33)2	5817.88
148.7	(148.7 - 154.33)2	31.64
193.8	(193.8 - 154.33)2	1558.28
Итого		13134.8

Определим групповую (частную) дисперсию для 2-ой группы:

Расчет для группы: 1 - 1.48 (21,22,23,24,25,26)

Таблица 2.7

Расчетная таблица

yj	(yj - yср)2	Результат
165.5	(165.5 - 143.53)2	482.53
142.2	(142.2 - 143.53)2	1.78
148.5	(148.5 - 143.53)2	24.67
126.9	(126.9 - 143.53)2	276.67
103.5	(103.5 - 143.53)2	1602.67
174.6	(174.6 - 143.53)2	965.14
Итого		3353.45

Определим групповую (частную) дисперсию для 3-ой группы:

Расчет для группы: 1.48 - 1.97 (27,28)

Таблица 2.8

Расчетная таблица

yj	(yj - yср)2	Результат
143.8	(143.8 - 161.9)2	327.61
	(180.0 - 161.9)2	327.61
Итого		655.22

Определим групповую (частную) дисперсию для 4-ой группы:

Расчет для группы: 1.97 - 2.45 (29)

Таблица 2.9

Расчетная таблица

yj	(yj - yср)2	Результат
127.8	(127.8 - 127.8)2
Итого

Определим групповую (частную) дисперсию для 5-ой группы:

Расчет для группы: 2.45 - 2.93 (30)

Таблица 2.10

Расчетная таблица

yj	(yj - yср)2	Результат
174.7	(174.7 - 174.7)2
Итого

Определим групповую (частную) дисперсию для 6-ой группы:

3. Внутригрупповые дисперсии объединяются в средней величине внутригрупповых дисперсий:

Средняя из частных дисперсий:

4. Межгрупповая дисперсия относится на счет изучаемого фактора, она называется факторной

δ² = ((158.94-154.31)²*12 + (154.33-154.31)²*8 + (143.53-154.31)²*6 + (161.9-154.31)²*2 + (127.8-154.31)²*1 + (174.7-154.31)²*1 +...)/30 = 72.93

Определяем общую дисперсию по всей совокупности, используя правило сложения дисперсий:

σ² = 1555.23 + 72.93 = 1628.17

Проверка:

Проверим этот вывод путем расчета общей дисперсии обычным способом:

Таблица 2.11

Расчетная таблица

yi	(yi - yср)2	Результат
59.2	(59.2 - 154.31)2	9046.55
242.4	(242.4 - 154.31)2	7759.26
	(218.0 - 154.31)2	4055.99
	(196.0 - 154.31)2	1737.78
158.6	(158.6 - 154.31)2	18.38
145.2	(145.2 - 154.31)2	83.05
152.7	(152.7 - 154.31)2	2.6
149.9	(149.9 - 154.31)2	19.48
125.8	(125.8 - 154.31)2	813.01
88.9	(88.9 - 154.31)2	4278.9
189.5	(189.5 - 154.31)2	1238.1
181.1	(181.1 - 154.31)2	717.53
143.5	(143.5 - 154.31)2	116.93
123.9	(123.9 - 154.31)2	924.97
173.7	(173.7 - 154.31)2	375.84
124.6	(124.6 - 154.31)2	882.88
95.8	(95.8 - 154.31)2	3423.81
230.6	(230.6 - 154.31)2	5819.66

продолжение таблицы 2.11

148.7	(148.7 - 154.31)2	31.51
193.8	(193.8 - 154.31)2	1559.2
165.5	(165.5 - 154.31)2	125.14
142.2	(142.2 - 154.31)2	146.73
148.5	(148.5 - 154.31)2	33.79
126.9	(126.9 - 154.31)2	751.49
103.5	(103.5 - 154.31)2	2581.99
174.6	(174.6 - 154.31)2	411.55
143.8	(143.8 - 154.31)2	110.53
	(180.0 - 154.31)2	659.8
127.8	(127.8 - 154.31)2	702.96
174.7	(174.7 - 154.31)2	415.62
Итого		48845.03

4.

Рис. 7 Поле корреляции и уравнение линейной регрессии

Для расчета параметров регрессии построим расчетную таблицу

Таблица 2.12

Расчетная таблица для нахождения параметров регрессии

x	y	x2	y2	x • y
0.61	124.6	0.37	15525.16	76.01
0.38	152.7	0.14	23317.29	58.03
2.04	127.8	4.16	16332.84	260.71
1.96		3.84		352.8
1.67	143.8	2.79	20678.44	240.15
1.08	142.2	1.17	20220.84	153.58
0.49	125.8	0.24	15825.64	61.64
1.44	174.6	2.07	30485.16	251.42
1.14	148.5	1.3	22052.25	169.29
1.31	126.9	1.72	16103.61	166.24
1.35	103.5	1.82	10712.25	139.73
0.94	148.7	0.88	22111.69	139.78
0.49	88.9	0.24	7903.21	43.56
0.19		0.0361		37.24
0.98	193.8	0.96	37558.44	189.92
0.43	149.9	0.18	22470.01	64.46
0.09		0.0081		19.62
0.29	158.6	0.0841	25153.96	45.99
0.08	242.4	0.0064	58757.76	19.39
0.03	59.2	0.0009	3504.64	1.78
0.7	95.8	0.49	9177.64	67.06
0.56	123.9	0.31	15351.21	69.38
0.7	230.6	0.49	53176.36	161.42
1.06	165.5	1.12	27390.25	175.43
0.49	189.5	0.24	35910.25	92.86
0.49	181.1	0.24	32797.21	88.74
0.31	145.2	0.0961	21083.04	45.01
0.58	173.7	0.34	30171.69	100.75
0.54	143.5	0.29	20592.25	77.49
2.93	174.7	8.58	30520.09	511.87
25.35	4629.4	34.24	763223.18	3881.33

Параметры уравнения регрессии.

Выборочные средние.

Выборочные дисперсии:

Среднеквадратическое отклонение

Коэффициент корреляции

Ковариация.

Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле:

Линейный коэффициент корреляции принимает значения от –1 до +1.

Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:

0.1 < r_xy < 0.3: слабая;

0.3 < r_xy < 0.5: умеренная;

0.5 < r_xy < 0.7: заметная;

0.7 < r_xy < 0.9: высокая;

0.9 < r_xy < 1: весьма высокая;

В нашем примере связь между признаком Y фактором X слабая и обратная.

Кроме того, коэффициент линейной парной корреляции может быть определен через коэффициент регрессии b:

Уравнение регрессии (оценка уравнения регрессии).

Линейное уравнение регрессии имеет вид y = -2.38 x + 156.32

Коэффициентам уравнения линейной регрессии можно придать экономический смысл.

Коэффициент регрессии b = -2.38 показывает среднее изменение результативного показателя (в единицах измерения у) с повышением или понижением величины фактора х на единицу его измерения. В данном примере с увеличением на 1 единицу y понижается в среднем на -2.38.

Коэффициент a = 156.32 формально показывает прогнозируемый уровень у, но только в том случае, если х=0 находится близко с выборочными значениями.

Но если х=0 находится далеко от выборочных значений х, то буквальная интерпретация может привести к неверным результатам, и даже если линия регрессии довольно точно описывает значения наблюдаемой выборки, нет гарантий, что также будет при экстраполяции влево или вправо.

Подставив в уравнение регрессии соответствующие значения х, можно определить выровненные (предсказанные) значения результативного показателя y(x) для каждого наблюдения.

Связь между у и х определяет знак коэффициента регрессии b (если > 0 – прямая связь, иначе - обратная). В нашем примере связь обратная.