Простейшая элементарная деформация

Простейшей элементарной деформацией является относительное удлинение некоторого элемента:

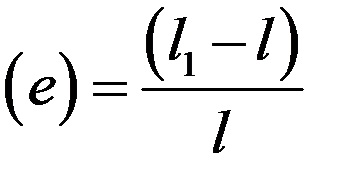
где 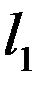- длина элемента после деформации,

- первоначальная длина этого элемента.

На практике чаще встречаются малые деформации, так что .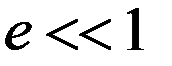

Характеристики деформации. Закон Гука, модуль Юнга, графики диффузии. Энергия упр. Диффузии.

Сила, действующая на единицу площади поперечного сечения S, называется напряжением:

δ=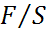

Количественной мерой, характеризующей степень деформации, испытываемой телом, является его относительная деформация.

ε =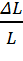

Английский физик Р.Гук экспериментально установил, что для малых деформаций относительное удлинение ε и напряжение δ прямо пропорциональны друг другу:

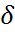=Eε,

Где коэффициент пропорциональности Е называется модулем Юнга.

Из вышеперечисленных формул следует:

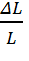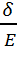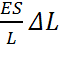ε = = = или F= =kΔL,

где k коэффициент упругости.Последнее выражение также задает закон Гука.

Вычислим потенциальную энергию сжатого стержня, которая равна работе, совершаемой внешними силами при деформации:

П=A= ,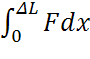

Где х – обсалютное удлинение стержня.Согласно закону Гука:

А=kx= .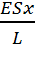

Поэтому

П= = ,

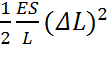Т.е. потенциальная энергия сжатого стержня пропорциональна квадрату деформации