 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Переходные процессы в синхронном электроприводе
|
|
Переходные процессы в синхронном электроприводе отличаются сложностью и большим многообразием, что определяется наличием не скольких магнитосвязанных обмоток, несимметрией магнитной системы, регулированием во многих режимах тока возбуждения.
В общем случае переходные процессы в синхронном электроприводе являются электромеханическими и описываются следующей системой уравнений:
 (5.4)
(5.4)
 (5.5)
(5.5)
 (5.6)
(5.6)
 (5.7)
(5.7)
 (5.8)
(5.8)
где  – напряжения, токи и сопротивление фазных обмоток;
– напряжения, токи и сопротивление фазных обмоток;
 – потокосцепления этих обмоток, определяемые индуктивностью и взаимной индуктивностью обмоток и токами, по ним протекающими.
– потокосцепления этих обмоток, определяемые индуктивностью и взаимной индуктивностью обмоток и токами, по ним протекающими.
Система уравнений (5.4) описывает электромагнитные процессы в цепях статора.
Уравнение (5.5) описывает переходный процесс в обмотке возбуждения СД. Если на роторе имеются другие обмотки, например успокоительные, то добавляются уравнения этих обмоток. Уравнение (5.6) дает общее выражение для электромагнитного момента синхронного двигателя, который в соответствии с теорией электрических машин определяется частной производной по геометрическому углу Qг=Q/ р от общего запаса электромагнитной энергии W эм. Электромагнитная энергия определяется полусуммой произведений потокосцеплений обмоток на их токи и находится с помощью (5.7). Для неявнополюсного СД выражение (5.6) в конечном виде для установившегося режима имеет вид (5.8). Уравнение (5.8) описывает механическое движение ротора синхронного двигателя. В него помимо электромагнитного (синхронизирующего) момента СД входят асинхронный момент М ас, создаваемый пусковой обмоткой, и момент нагрузки М с.
Система уравнений (5.4) – (5.8) позволяет анализировать все возможные виды переходных процессов, возникающих в синхронном электроприводе: пуск синхронного привода и его синхронизацию, изменение нагрузки на его валу и регулирование тока возбуждения. Обычно для упрощения анализа переходных режимов уравнения (5.4) –(5.8) преобразуются к более простым, записанным относительно новых переменных и не содержащим при них периодических коэффициентов. Наиболее распространена форма записи этих преобразованных выражений в виде уравнений Парка-Горева. Несмотря на упрощения, получаемые в результате подобных преобразований уравнений, для их решения необходимо использование ЭВМ.
Аналитическими методами могут быть проанализированы лишь простейшие переходные процессы при принятии ряда допущений. В качестве примера рассмотрим переходный процесс в синхронном приводе, связанный с небольшими изменениями скорости и внутреннего неявнополюсного СД без учета электромагнитных переходных процессов.
Переходный процесс в этом случае относится к классу механических и описывается уравнением (5.8). При малых изменениях скорости и угла входящие в него моменты, синхронизирующей М и асинхронный M ac, могут быть представлены в следующем упрощенном виде:
 (5.9)
(5.9)
 (5.10)
(5.10)
где b – жесткость механической характеристики СД, обусловленной пусковой обмоткой.
В результатеуравнение (5.8) ротора СД при малых изменениях координат его движения принимает вид
 (5.11)
(5.11)
Характеристическое уравнение, соответствующее (5.11), и его корни запишутся в виде
 (5.12)
(5.12)
 (5.13)
(5.13)
где 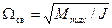 – частота свободных колебаний СД;
– частота свободных колебаний СД;
 – механическая постоянная времени СД, определяемая асинхронной пусковой обмоткой.
– механическая постоянная времени СД, определяемая асинхронной пусковой обмоткой.
Из (5.13) следует, что при  корни характеристического уравнения вещественные и отрицательные и переходный процесс имеет апериодический характер. При обратном соотношении этих параметров, т. е. при
корни характеристического уравнения вещественные и отрицательные и переходный процесс имеет апериодический характер. При обратном соотношении этих параметров, т. е. при  характеристическое уравнение (5.12) имеет комплексные корни, в соответствии с чем переходные процессы имеют колебательный характер.
характеристическое уравнение (5.12) имеет комплексные корни, в соответствии с чем переходные процессы имеют колебательный характер.
Частота этих затухающих колебаний W определяется выражением
 (5.14)
(5.14)
а степень успокоения колебаний характеризуется величиной a=1/ Т м,ас. Чем меньше Т м,ас, т. е. чем больше жесткость b пусковой характеристики, тем быстрее затухают колебания. При b=0 затухание отсутствует и СД совершает свободные колебания с частотой Wсв.
Общее решение уравнения (5.11) имеет вид
 (5.15)
(5.15)
где постоянная Qм, и сдвиг фазы y определяется в зависимости от начальных условий для конкретного переходного процесса.
На рис. 5.8. в качестве примера показаны графики переходного процесса при вхождении СД в синхронизм, которые могут быть получены с помощью (5.15).

Рис. 5.8. Графики переходного процесса вхождения в синхронизм СД
Дата публикования: 2015-10-09; Прочитано: 745 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
