Силы и напряжения в поперечных сечениях бруса

Растяжение (сжатие) – это вид нагружения бруса, при котором в его поперечных сечениях возникает только один внутренний силовой фактор – продольная сила N.

При растяжении и сжатии внешние силы приложены вдоль продольной оси z (рисунок 109).

Рисунок 109

Применяя метод сечений, можно определить величину ВСФ – продольную силу N при простом нагружении .

Внутренние силы (напряжения), возникающие в произвольном поперечном сечении при растяжении (сжатии), определяются с помощью гипотезы плоских сечений Бернулли:

сечение бруса, плоское и перпендикулярное оси до нагружения, остается таким же и при нагружении.

Отсюда следует, что волокна бруса (рисунок 110) удлиняются на одинаковые величины. Значит внутренние силы (т.е. напряжения), действующие на каждое волокно будут одинаковы и распределены по сечению равномерно.

Рисунок 110

Так как N – равнодействующая внутренних сил, то N = σ · А, згачит нормальные напряжения σ при растяжении и сжатии определяются по формуле:

[Н/мм² = МПа], (72)

где А – площадь поперечного сечения.

Пример 24. Два стержня: круглого сечения диаметром d = 4 мм и квадратного сечения со стороной 5 мм растягиваются одинаковой силой F = 1000 Н. Какой из стержней больше нагружен?

Дано: d = 4 мм; а = 5 мм; F = 1000 Н.

Определить: σ₁ и σ₂ – в стержнях 1 и 2.

Решение:

При растяжении продольная сила в стержнях N = F = 1000 Н.

Площади поперечных сечений стержней:

; .

Нормальные напряжения в поперечных сечениях стержней:

, .

Так как σ₁ > σ₂, то первый стержень круглого сечения нагружен больше.

Пример 25. Трос, свитый из 80 проволочек диаметром 2 мм растягивается силой 5 кН. Определить напряжение в поперечном сечении.

Дано: к = 80; d = 2 мм; F = 5 кН.

Определить: σ.

Решение:

N = F = 5 кН, ,

тогда .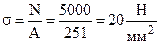

Здесь А₁ – площадь сечения одной проволочки.

Примечание: сечение троса – не круг!

2.2.2 Эпюры продольных сил N и нормальных напряжений σ по длине бруса

Для расчетов на прочность и жесткость сложно нагруженного бруса при растяжении и сжатии необходимо знать значения N и σ в различных поперечных сечениях.

Для этого строятся эпюры: эпюра N и эпюра σ.

Эпюра – это график изменения продольной силы N и нормальных напряжений σ по длине бруса.

Продольная сила N в произвольном поперечном сечении бруса равна алгебраической сумме всех внешних сил, приложенных к оставшейся части, т.е. по одну сторону от сечения

(73)

Внешние силы F, растягивающие брус и направленные в сторону от сечения, считаются положительными.

Порядок построения эпюр N и σ

1 Поперечными сечениями разбиваем брус на участки, границами которых являются:

а) сечения на концах бруса;

б) где приложены силы F;

в) где меняется площадь сечения А.

2 Нумеруем участки, начиная со

свободного конца.

3 Для каждого участка, используя метод

сечений определяем продольную силу N

и строим в масштабе эпюру N.

4 Определяем нормальное напряжение σ

на каждом участке и строим в

масштабе эпюру σ.

Пример 26. Построить эпюры N и σ по длине ступенчатого бруса (рисунок 111).

Дано: F₁ = 10 кН; F₂ = 35 кН; А₁ = 1 см²; А₂ = 2 см².

Решение:

1) Разбиваем брус на участки, границами которых являются: сечения на концах бруса, где приложены внешние силы F, где меняется площадь сечении А – всего получилось 4 участка.

2) Нумеруем участки, начиная со свободного конца:

с I по IV. Рисунок 111

3) Для каждого участка, используя метод сечений, определяем продольную силу N.

Продольная сила N равна алгебраической сумме всех внешних сил, приложенных к оставшейся части бруса . Причем внешние силы F, растягивающие брус считаются положительными.

Таблица 13

Участок	Оставшаяся часть	N
I		NI = 0
II		NII = F1 = 10 кН
III		NIII= F1 = 10 кН
IV		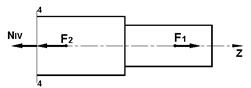NIV=F1 – F2=10-35= = -25 кН

4) Строим в масштабе эпюру N. Масштаб указываем только положительными величинами N, на эпюре знак «плюс» или «минус» (растяжение или сжатие) указывается в кружочке в прямоугольнике эпюры. Положительные величины N откладываются выше нулевой оси эпюры, отрицательные – ниже оси.

5) Проверка (устная): В сечениях, где приложены внешние силы F, на эпюре N будут вертикальные скачки, равные по величине этим силам.

6) Определяем нормальные напряжения в сечениях каждого участка :

; ;

; .

Строим в масштабе эпюру σ.

7) Проверка: Знаки N и σ одинаковы.

Подумай и ответь на вопросы

52 Можно ли считать, что поперечные сечения бруса остаются при растяжении плоскими и перпендикулярными оси?

1) нельзя; 2) можно.

53 Зависят ли напряжения при растяжении (сжатии) стержней от формы их поперечного сечения (квадрат, прямоугольник, круг и др.)?

1) зависят; 2) не зависят.

54 Зависит ли величина напряжения в поперечном сечении от материала, из которого изготовлен стержень?

1) зависит; 2) не зависит.

55 Какие точки поперечного сечения круглого стержня нагружены больше при растяжении?

1) на оси бруса; 2) на поверхности круга;

3) во всех точках сечения напряжения одинаковы.

56 Стержни из стали и дерева с равной площадью поперечного сечения растягиваются одинаковыми силами. Будут ли равны возникающие в стержнях напряжения?

1) в стальном напряжение больше;

2) в деревянном напряжение больше;

3) в стержнях возникнут равные напряжения.

57 Для бруса (рисунок 112) построить эпюры N и σ, если F₁ = 2 кН; F₂ = 5 кН; А₁ = 1,2 см²; А₂ = 1,4 см².

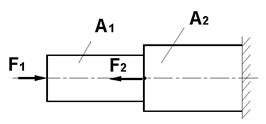
Рисунок 112