Сложение и вычитание. Сначала рассматриваются те упражнения на сложение и вычи­тание, в которых сумма минут (секунд) меньше

Сначала рассматриваются те упражнения на сложение и вычи­тание, в которых сумма минут (секунд) меньше, чем 60, сумма часов меньше, чем 24, сумма месяцев меньше, чем 12.

1) 3 ч+5 ч=8 ч 8 мес.+З мес. =

23 ч-11 ч=12 4 мес. 28 мин-19 мин=9 мин

мин 3 ч 17 мин—17 мин=3 4 3 4 17 мин—3 4=17 мин

2) 3 ч+17 мин=3 ч 17

3)	3 ч 20 мин + 30 мин	10 мин 25 с 5 мин	12 ч 35 мин + 8 ч 12 мин
3 ч 50 мин 3 ч 20 мин ~~ 10 мин	15 мин 2Й с 10 мин 25 с "~ 7 мин	20 ч 47 мин 23 ч 25 мин ~~17 ч 17 мин
3 ч 10 мин	3 мин 21) с	6ч 8 мин

Выполнение упражнений такого вида можно проводить и устно '•{•а записи или с записью в строчку. Они, как правило, включают-и в устный счет.

После этого рассматриваются более сложные упражнения, в ноторых сумма минут (секунд) равна или больше 60, сумма часов больше 24, сумма месяцев больше, чем 12, и т. д., и при вычита­нии крупные меры необходимо выразить в мелких.

Рассмотрение таких упражнений целесообразно проводить в гакой последовательности: I) 35 мин+25 мин=60 мин=1 ч 1 ч—45 мин=15 мин

"• 1 С

60 мин—45 мин=15 мин

2) 35 мин+45 мин=80 мин=1 ч 20 мин

1 ч 20 мин—45 мин=35 мин

1 ч=60 мин

60 мин+20 мин=80 мин

80 мин—45 мин=35 мин

3 ч 20 мин+30 мин=3 ч 50 мин 3 ч 20 мин+2 ч=5 ч 20 мин

|3 ч 50 мин—30 мин=3 ч 20 мин 3 ч 50 мин—2 ч= 1 ч 50 мин

О Ч ^\_/ 1ПГ111 I — * —

(Складываются и вычитаются числа одного наименования.)

4 и-40мин=3ч20мин

Я и 20 мин+40 мин=4 ч

4 ч=3 ч 60 мин 3 ч 60 мин ~~ 40 мин 3 ч 20 мин

20 мин+40 мин=60 мин= 1 ч

Зч+1ч=4ч

: ч 10 мин—50 мин=3 ч 20 мин

3 ч 20 мин4-50 мин=4 ч 10 мин

4 ч 10 мин=3 ч 70 мин _3 ч 70 мин ~ 50 мин 3 ч 20 мин

20 мин+50 мин=70 мин=

= 1 ч 10 мин

3 ч+1 ч 10 мин=4 ч 10 мин

ю*

4)Зч20мин+1 ч 15мин= =4 ч 35 мин

4 ч 35 мин—1 ч 15 мин= =3 ч 20 мин

5) 3 ч 20 мин+1 ч 40 мин=4 ч 60 мин=5 ч

3 ч 20 мин+1 ч 55 мин=4 ч 75 мин=5 ч 15 мин 5 ч 15 мин—1 ч 55 мин=

1-й способ.. 75 _5 ч Ьй'мин 1 ч об мин

2-й способ.

5 ч 15 мин=4 ч 75 мин

4 ч 75 мин—1 ч 55 мин=3 ч 20 мин

3 ч 20 мин

Арифметические действия с числами, выраженными в мера] времени и мерах метрической системы, сравниваются, устанавл! ваются их сходство и различие.

Например: «Реши примеры, объясни их решение. В чем схода во и в чем различие решения этих примеров?»

Зч 58 мин,3р. 58 к. _7м40см _7ч 40 мт
1 ч 46 мин 1 р. 46 к. 1 м 50 см 1 ч 50 ми»

Вопросы и задания

1.Каковы дидактические требования изучения единиц измерения време
ни, развития временных представлений учащихся с интеллектуальным недо
развитием?

2. Составьте фрагмент одного из уроков по ознакомлению учащихся
единицами измерения времени: час, минута, год.

3. Сравните решение примеров: 535—248, 5 р. 35 к.—2 р. 48 к.|
5 ч 35 мин—2 ч 48 мин. Какой из этих примеров вызовет наибольший
трудности у учащихся? Почему?

4. На примерах из учебников математики покажите задания, направлен­
ные на развитие мышления и речи учащихся при развитии временных пред­
ставлений.

Глава 17 МЕТОДИКА ИЗУЧЕНИЯ ОБЫКНОВЕННЫХ ДРОБЕЙ

К моменту изучения долей, а затем и обыкновенных дробей у школьников с нарушением интеллекта имеется уже некоторый жизненно-практический опыт в образовании и наблюдении долей целых предметов или величин.

В играх, в своей практической деятельности они сталкивались с потребностью разделить целый предмет на равные части, напри-292

•р. распилить доску пополам, отрезать половину или четверть |нты, тесьмы, разрезать репу, булку, яблоко на две или четыре |вные части, разделить пополам конфету, разделить на две, три, «тыре равные части отрезок и т. д.

\ Однако при изучении дробей учащиеся встречаются со многи-ци новыми свойствами и качествами дробных чисел, значительно Отличающими их от натуральных: название, запись, возможность Исполнения таких преобразований над дробями, которые изменят |нешний вид дроби, но дробь останется равной данной.

Новизна этого раздела математики, а также его жизненно-Практическая значимость вызывают у учащихся большой интерес. Это объясняется использованием при изучении дробей большого:количества наглядных пособий, дидактического материала, акти-! визацией практической деятельности учащихся.

Изучение обыкновенных дробей расширяет представление ум­ственно отсталых школьников о числах. Учащиеся узнают, что, кроме целых чисел, существуют еще и дробные, которые обладают особыми свойствами, отличными от свойств целых чисел, а изуче­ние арифметических действий с дробями убеждает их, что дроби, как и целые числа, можно складывать, вычитать, умножать, де­лить, что все действия над дробными числами подчиняются тем же законам, что и действия над целыми числами. На примере изучения дробей учитель имеет возможность показать то общее, что свойственно всем числам, и то особенное, что свойственно только дробным числам. Все это способствует развитию наблюда­тельности, внимания, формированию логического мышления, уме­ния находить причинные связи и т. д.

Изучение дробей способствует развитию речи, обогащению словаря учащихся новыми словами и выражениями: разделить на равные части, пополам, доля, дробь, смешанное число, числитель, знаменатель, сократить, привести к наименьшему общему знаме­нателю и др.

Велико для учащихся с нарушением интеллекта жизненно-практическое значение изучения дробей. С дробными числами в форме обыкновенных дробей учащимся приходится сталкиваться в школьных мастерских (столярной, слесарной, переплетной, швей­ной и т. д.), на производственной практике. Незнание дробей может задержать овладение профессией, затруднит ориентацию выпускников школы VIII вида в повседневной жизни.

На уроках, где учащиеся получают первоначальное предс' ние об образовании, преобразованиях, свойствах дробей и д< виях над ними, совершенно необходимо использовать доста количество наглядных пособий, дидактического материала.. этом учитель не только организует наблюдения учащихся, т включает их в активную практическую деятельность с дидакти'мч] ким материалом, а затем углубляет и конкретизирует предстанл* ние о дробных числах при решении жизненно-практических задач Например, выполняются такие задания: отпилить -^ (половину доски, отогнуть -т часть картонного листа для приготовления КС робки, вырезать шесть шестых долей круга, сшить их и образе вать донышко берета и т. д. Таким образом, доли ^, р ^ конкре тизируются в представлении учащихся.

Какие же наглядные пособия и дидактический материал целе сообразно использовать при изучении обыкновенных дробей?

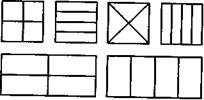
Рис. 22

Это такие пособия: предм«ты, которые легко разделить равные части, например: яблс ко, торт, репа, арбуз, апельси^ и т. д.; при делении этих пре метов на части образуются доли, значительно отличаю! щиеся от целого, — это поле вина, четверть яблока (апель| сина); макеты предметов или шара, разделенных на равные части;

фанерные, картонные, бумажные круги, разделенные на равные части;

квадраты, прямоугольники, полоски, разделенные на равные части (рис. 22);

классные счеты с вертикальными прутьями и набором долей единицы;

таблицы с рисунками предметов, кругов, квадратов, прямо­угольников, отрезков, разделенных на равные части;

таблицы с долями и названиями долей;

таблицы, иллюстрирующие сравнение обыкновенных дробей между собой, сравнение их с единицей, преобразования обыкно­венных дробей и действия над ними.