Геометричні параметри різальної частини косозубых зуборізних гребінок

Статичні геометричні параметри косозубой зуборізної гребінки

Косозубая зуборізна гребінка (рис. 4.11) має плоску передню поверхню, яка розташовується паралельно торцю нарізуваного зубчатого колеса. В процесі обробки гребінка здійснює головний зворотно-поступальний рух різання, швидкість `V якого направлена під кутом w до осі нарізуваного колеса.

Рисунок 4.11 – Косозуба зуборізна гребінка.

Гребінка має вершинну різальну кромку і дві бічні різальні кромки, положення яких визначається кутом a_S.

Задня поверхня косозубой гребінки є сукупністю задніх площин на вершинній і бічних різальних кромках. Задню поверхню можна вважати фасонною циліндровою поверхнею, твірні якою йдуть під кутом r.

Виберемо систему координат XYZ. Направимо вісь Z перпендикулярно передній площині гребінки, вісь Х – по вершинній різальній кромці гребінки. У вибраній системі координат XYZ вектор `V статичної швидкості різання буде:

. (4.298)

Вектор `Р₁ що йде по вершинній різальній кромці буде:

. (4.299)

Вектор `Р₂, що йде по бічній різальній кромці АВ, буде:

. (4.300)

Вектор `Р₃, що йде по бічній різальній кромці EF, буде:

. (4.301)

Вектор нормали `N_П до передньої площини

. (4.302)

Статичний кут l_с нахилу різальної кромки визначається за залежностю:

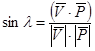. (4.303)

Відповідно до цієї формули для бічної різальної кромки АВ матимемо:

. (4.304)

Для вершинної кромки

, (4.305)

Тобто

.

Статичний передній кут g_нс, в нормальному до різальної кромки перетині, визначається по залежності:

. (4.306)

Вектор нормали `N_р до статичної площини різання для вершинної кромки буде:

. (4.307)

Скалярний добуток векторів `N<sub>р</sub> та `N_П буде рівний нулю. Звідси статичний передній кут g_нс на вершинній кромці буде рівний нулю.

Вектор нормали `N_р до статичної площини різання для бічної різальної кромки АВ буде:

. (4.308)

Скалярний добуток векторів `N<sub>р</sub> та `N_П буде:

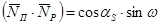. (4.309)

Векторний добуток векторів `N<sub>р</sub> та `N_П буде:

. (4.310)

Розкриваючи визначник, отримаємо:

. (4.311)

Модуль векторного добутку буде:

. (4.312)

Таким чином, статичний передній кут g_нс на бічній різальній кромці АВ в нормальному перетині буде:

. (4.313)

Для другої бічної різальної кромки EF статичний передній кут g_нс буде:

. (4.314)

Статичний задній кут a_нс в нормальному до різальної кромки перерізі визначається по залежності:

. (4.315)

У системі XYZ вектор `З, що йде по твірній задній поверхні, буде:

. (4.316)

Вектор нормали `N_з до задньої поверхні для вершинної різальної кромки буде:

. (4.317)

Скалярний добуток векторів `N<sub>р</sub> та `N_з буде:

. (4.318)

Векторний добуток векторів `N<sub>р</sub> та `N_з буде:

. (4.319)

Модуль векторного добутку буде:

. (4.320)

Таким чином, на вершинній різальній кромці гребінки статичний кут a_Н буде рівний:

. (4.321)

. (4.322)

Вектор нормали `N_з до задньої площини на бічній різальній кромці АВ буде рівний:

. (4.323)

Скалярний добуток векторів `N<sub>р</sub> та `N_з буде:

. (4.324)

Векторний добуток векторів `N<sub>р</sub> та `N_з буде:

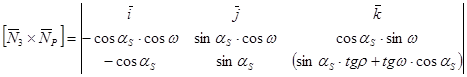. (4.325)

Розкриваючи визначник і перетворюючи отримаємо:

. (4.326)

Модуль векторного добутку буде:

. (4.327)

Таким чином, на бічній різальній кромці АВ статичний задній кут a_нс буде рівний:

. (4.328)

Для вершинної кромки при a_S=90° матимемо tga_нс=tgr. Цей же результат був отриманий при безпосередньо розглянуті вершинної кромки. На другій бічній різальній кромці EF кут a_S має негативне значення.

. (4.329)

Аналіз показує, що різниця між величинами задніх кутів на різних бічних різальних кромках невелика. Передні ж кути g_нс на різних бічних різальних кромках істотно відрізняються один від одного. Для поліпшення умов різання доцільно на кромці з позитивними передніми кутами знімати фаски і зменшувати величину переднього кута g_нс, а на другій бічній кромці з негативними передніми кутами проводити вишліфовку канавки на передній поверхні і таким чином збільшувати передні кути.