Задачи для самостоятельного решения. Задача 1. Преобразовать в СДНФ булеву функцию, заданную формулой

Задача 1. Преобразовать в СДНФ булеву функцию, заданную формулой

а) f=( ® у)(zÅ );

б) f= ;

в) f=( ®z)V(y® ).

Задача 2. По таблице истинности получить СДНФ булевой функции

а) f=(x ® )(z® );

б) f= .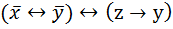

§ 2. Совершенная конъюнктивная нормальная форма (СКНФ)

Существует и другая нормальная форма (конъюнктивная).

Выражение (отрицание на любых местах) называется элементарной дизъюнкцией (ЭД).

Конъюнкция нескольких ЭД называется конъюнктивной нормальной формой (КНФ).

Если к тому же все ЭД правильны и полны, то КНФ называется совершенной (СКНФ).

Рассмотрим способ получения СКНФ с помощью СДНФ.

Пусть дана булева функция f(x₁…x_n). Двойственной булевой функцией называется булева функция f*, заданная формулой

f*(x₁…x_n)=

Заметим, что (f*)*=f.

Например, для f=x V y двойственной является f* = = xy.

Таким образом, двойственной к дизъюнкции является конъюнкция и наоборот.

Теорема (закон двойственности). Двойственная к композиции булевых функций есть соответствующая композиция двойственных булевых функций (композиция булевых функций – сложная функция, составленная из нескольких булевых функций).

Следствие 1. Если в формуле присутствует только дизъюнкция, конъюнкция и отрицания, то для получения достаточно заменить дизъюнкцию конъюнкцией и наоборот.

Следствие 2. Двойственной к СДНФ является СКНФ.

Из следствия 2 вытекает практический алгоритм преобразования данной формулы в СКНФ, используя двойственность:

1) найти f*;

2) преобразовать f* в СДНФ;

3) еще раз взять двойственную. (f*)*=f= СДНФ*=СКНФ.

Аналогично тому, как с помощью таблицы истинности была получена СДНФ, можно получить СКНФ. Для этого в последнем столбце таблицы выбираем нули, а в исходных наборах 0 заменим переменной, 1 – отрицанием переменной.