 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Понятие о полноте системы функций алгебры логики
|
|
Система элементарных булевых функций j 1, j 2,..., jm называется функционально полной, если любую функцию алгебры логики можно представить в виде суперпозиции этих функций.
Примером функционально полной системы элементарных булевых функций служит система трех функций: 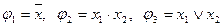 . Это следует из того, что любую функцию алгебры логики можно представить в виде формулы с помощью конъюнкции, дизъюнкции и отрицания (4).
. Это следует из того, что любую функцию алгебры логики можно представить в виде формулы с помощью конъюнкции, дизъюнкции и отрицания (4).
Однако это не единственная функционально полная система. Примерами функционально полных систем элементарных функций также являются:
1) 
2) 
3)  ;
;
4) 
5) 
6) 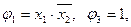
И другие
Доказательством полноты приведенных выше систем элементарных функций может служить возможность сведения любой из них к функционально полной системе из трех элементарных функций  .
.
Дата публикования: 2015-09-18; Прочитано: 317 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
