Таблицы истинности для логических функций двух переменных Обозначение функции и выражение через операции И, ИЛИ, НЕ
х 1
Название
Специальное обозначение
Чтение
х 2
f 0 = 0
Константа «0»
Всегда «0»
f 1 = х 1 х 2
Конъюнкция
х 1 х 2
х 1 и х 2
f 2 =
Запрет по х 2
Неверно, что если х 1 , то х 2
f 3 = х 1
Переменная х 1
х 1
f 4 =
Запрет по х 1
Неверно, что если х 2 , то х 1
f 5 = х 2
Переменная х 2
х 2
f 6 =
Сложение по модулю 2
х 1 Å х 2
х 1 неравнозначно х 2
f 7 = х 1 Ú х 2
Дизъюнкция
х 1 Ú х 2
х 1 или х 2
f 8 =
Функция (стрелка) Пирса
x 1 ¯ x 2
Ни х 1 , ни х 2
f 9 =
Эквивалентность
x 1 «x 2
х 1 равнозначно х 2
f 10 =
Инверсия х 2
Не х 2
f 11 =
Импликация
x 2 ® x 1
Если х 2 , то х 1
f 12 =
Инверсия х 1
Не х 1
f 13 =
Импликация
x 1 ® x 2
Если х 1 , то х 2
f 14 =
Функция (штрих) Шеффера
x 1 / x 2
Неверно, что х 1 и х 2
f 15 = 1
Константа «1»
Всегда «1»
Дата публикования: 2015-09-18 ; Прочитано: 414 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
studopedia.org - Студопедия.Орг - 2014-2026 год. Студопедия не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования
(0.374 с) ... 

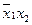
 Ú
Ú 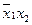
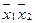
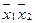 Ú
Ú 


 Ú
Ú 


 Ú
Ú 
 Ú
Ú 
