Метод искусственного базиса

Позволяет объединить оба этих этапа в одном за счет введения дополнительных переменных как в ограничениях, так и в целевую функцию. Вместо исходной канонической задачи ЛП рассматривается расширенная задача:

(n>m)

где M – достаточно большое положительное число,

при ограничениях:

();

(); ().

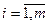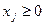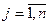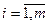Для расширенной задачи исходное допустимое базисное решение очевидно:

(); ().

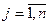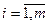Значение целевой функции для этого решения .

Введение в целевую функцию коэффициентов – M при дополнительных переменных эквивалентно введению «штрафа» за включение в базисное решение переменных (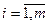). Поэтому числа – M, которые по абсолютной величине значительно больше остальных коэффициентов целевой функции, позволяют выводить из базиса дополнительные переменные, заменяя их переменными исходной задачи. Поэтому метод имеет еще одно название – «больших штрафов».

Таким образом, если в результате решения расширенной задачи получено оптимальное решение вида:

(); (),

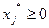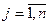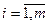где все дополнительные переменные равны нулю, то вектор дает оптимальный результат исходной задачи, для которой .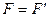

Если оптимальное решение расширенной задачи содержит хотя бы одну положительную дополнительную переменную , то исходная задача не имеет допустимых базисных решений, т. к. ее ограничения не совместимы.

Пример использования метода искусственного базиса.

Исходная задача:

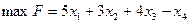
при ограничениях:

Расширенная задача:

Представим целевую функцию в виде двух групп слагаемых (с множителем M и без него):

Перепишем для записи в симплекс – таблицу в виде двух строк:

Симплекс – таблица:

Номер итерации	F, 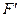и базовая переменная	Значения
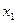
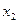
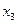
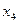
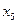
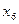
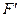
		-6M	-3 M	-5 M	-3 M	-3 M
	-5	-3	-4
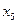
			3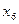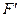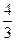
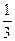		-M	- M		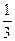M	M
	-4		-2
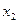
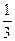
				-2
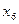
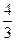
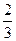
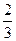
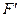
			-3
				-	-

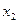
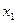
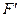
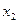
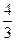
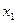
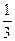
в точке (1,0,1,0) ит.к. значения переменных .

Двойственная задача ЛП.

Рассмотрим две следующие задачи:

Задача 1

при ограничениях:

();

().

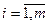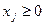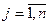Задача 2

при ограничениях:

();

().

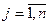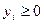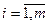Эти задачи образуют так называемую двойственную пару задач ЛП. Первая задача называется исходной, а вторая – двойственной.

В этих задачах используются одни и те же константы, однако исходная задача является задачей максимизации, а двойственная – задачей минимизации. Число переменных двойственной задачи равно числу ограничений исходной и наоборот; знаки неравенств в ограничениях являются обратными; коэффициенты целевой функции одной задачи являются свободными членами ограничений другой.

Пример записи двойственной задачи:

Исходная задача

при ограничениях

Двойственная задача

при ограничениях

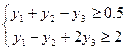
Между решениями исходной и двойственной задач существует точная связь, которую можно представить следующими свойствами:

1) Любое допустимое решение исходной задачи определяет оценку снизу для оптимального значения целевой функции двойственной задачи;

2) Любое допустимое решение двойственной задачи дает оценку сверху для целевой функции исходной задачи;

3) Для оптимальных решений прямой и двойственной задач значения целевых функций совпадают.

Есл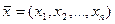и и - допустимые решения прямой и двойственной задач соответственно, то первые два свойства означают, что всегда выполняется неравенство

Для оптимальных решений и справедливо выражение

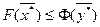
Чтобы доказать эти положения: 1) умножим каждое i – е ограничение прямой задачи на , наоборот, каждое j – е ограничение двойственной задачи на .

Так как 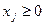(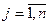) и 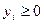(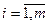), то знаки не изменяются:

();

();

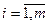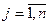Суммируем все соотношения в каждой группе:

или .

Для доказательства полученного положения отметим, что неравенство выполняется также и для оптимального решения двойственной задачи , т. е.

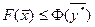
При этом, как следует из постановки прямой задачи справедливо неравенство

Отсюда получаем, что .

Аналогичные рассуждения можно привести и для оптимального решения исходной задачи , для которого

Одновременно имеем, что . Отсюда также получаем, что .