Симплекс – метод решения задачи ЛП

Является основным методом решения задач ЛП, представленных в канонической форме записи.

Разработан в 1949 г. американским математиком Дж. Данценгом.

Идея симплекс – метода заключается в следующем.

Сначала выбирается одно из допустимых базисных решений, соответствующее некоторой вершине многогранника.

Для этого свободные переменные приравниваются к нулю и решается система уравнений, образованная ограничениями.

Если при этом некоторые из базисных переменных окажутся отрицательными, то необходимо выбрать другие свободные переменные, т. е. перейти к новому базису.

Далее для полученного допустимого базисного решения проверяется: достигнут ли здесь экстремум целевой функции.

Если экстремум не достигнут, то осуществляется переход к ближайшему допустимому

базисному решению, соответствующему соседней вершине многогранника, для которой

значение целевой функции возрастает (при поиске max) или убывает (при поиске min).

Рассмотрим метод на примере:

при ограничениях

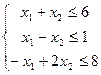
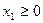
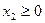
Если ввести дополнительные слабые переменные :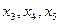

; ; ; ; .

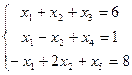
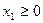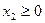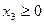Перепишем задачу в следующем виде

;

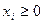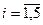
Общее число переменных m + n = 5, число уравнений в системе ограничений m = 3. Следовательно, в каждом базисном решении имеется две свободных и три базисных переменных.

Выберем в качестве свободных переменные 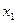и 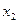. Приравняем их нулю и получим базисное решение:

; ; ; ; .

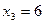Так как все переменные неотрицательны, то это решение является допустимым базисным решением, при котором значение целевой функции .

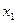Для полученного решения максимум целевой функции F не достигнут, т. к. в выражении для целевой функции обе свободные переменные и 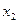входят с отрицательным знаком. Поэтому, увеличивая значение любой из них, можно получить большее значение целевой функции F.

Но увеличивать значение свободной переменной можно только путем ее перевода в базисные. При этом необходимо одну из базисных переменных перевести в свободные.

Укажем способ, по которому производится выбор таких переменных.

Для перевода из свободных переменных в базисную целесообразно выбрать такую переменную, которая входит в выражение для целевой функции F с наибольшим по абсолютной величине отрицательным коэффициентом. В данном примере это .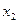

При возрастании свободной переменной некоторые из базисных переменных начнут уменьшаться. Так как отрицательные значения переменных недопустимы, то в качестве новой свободной переменной следует выбрать такую базисную переменную, которая раньше других принимает нулевое значение.

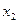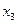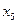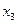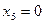При увеличении для уменьшаются значения переменных и . Переменная принимает нулевое значение при ; переменная при 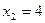. Следовательно, свободной переменной вместо 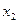должна стать переменная .

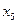Общее правило выбора: для определения базисной переменной, переводимой в свободную, вычисляются отношения свободного члена уравнения к коэффициенту при свободной переменной, переводимой в базисные. При этом отрицательные отношения не учитываются. В итоге выбирается базисная переменная, входящая в уравнение с наименьшим отношением.

В частности для второго уравнения:

для третьего: - неустойчивость

для четвертого: .

Таким образом, для перехода к новому допустимому базисному решению, увеличивающему значение F необходимо перевести:

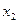- из свободных в базисные;

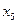- из базисных в свободные переменные.

Все уравнения задачи необходимо переписать таким образом, чтобы в последнем уравнении (где присутствует 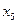) коэффициент при 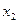стал равным единице, а в оставшихся строках – нулю.

Процедура, с помощью которой это достигается, называется сменой базиса и осуществляется следующим образом:

- уравнение, соответствующее базисной переменной, переводимой в свободные (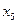), делится на коэффициент при свободной переменной, переводимой в базисные ();

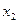- для каждого из оставшихся уравнений определяется коэффициент при свободной переменной , переводимой в базисные. Далее полученное на предыдущем шаге уравнение уменьшается на коэффициент (- ) и складывается с каждым i – м уравнением.

Продолжим пример:

После первого шага, называемого нормировкой:

После второго шага окончательно получаем:

Приравняв нулю свободные переменные получим новое допустимое базисное решение и значение целевой функции:

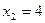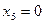; ; ; ; ;F=8.

Максимум целевой функции также не достигнут, т. к. в выражении для F переменная 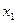входит с отрицательным знаком. Поэтому 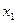следует перевести из свободных в базисные.

Чтобы определить базисную переменную, переводимую в свободные, вычисляется отношение свободных членов уравнений к коэффициентам при 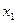(справа от уравнений). Выбирается строка с минимальным положительным отношением (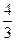). Базисная переменная из этой строки (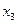) переводится в свободные.

Выполняем схему базиса и получаем:

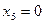; ; ; ; ;F=10.

Полученное допустимое базисное решение является решением задачи, т. к. при увеличении любой свободной переменной (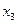, 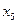) значение целевой функции может только уменьшаться. Это объясняется тем, что коэффициенты при свободных переменных в выражении для F положительны.

Таким образом, в качестве критерия оптимальности можно рассматривать знаки коэффициентов при свободных переменных в выражении целевой функции.

В случае задачи максимизации – это неотрицательные коэффициенты в выражении целевой функции; минимизации – неположительные.

С учетом сказанного общая схема решения задачи ЛП симплекс – методом имеет вид:

Начало

Выбор исходного

допустимого базиса

проверка

отличимости

решения

Нет Конец

Определение свободной переменной,

переводимой в базисные

Определение базисной переменной,

переводимой в свободные

Смена базиса