 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Решение. Расширенная матрица системы имеет вид
|
|
Здесь
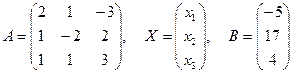 .
.
Расширенная матрица системы имеет вид
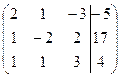 .
.
Выполним прямой ход метода Гаусса.
Шаг 1. Для удобства вычислений поменяем местами первую и вторую строки:
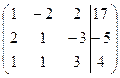 .
.
Так как 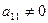 , то умножая первую строку на (-2) и на (-1) и прибавляя полученные строки соответственно ко второй и третьей строкам, исключим переменную
, то умножая первую строку на (-2) и на (-1) и прибавляя полученные строки соответственно ко второй и третьей строкам, исключим переменную 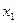 из всех строк, начиная со второй:
из всех строк, начиная со второй:
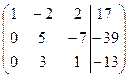 .
.
Шаг 2. Так как 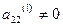 , то умножим вторую строку на (-3/5) и прибавим к третьей, таки образом исключим переменную
, то умножим вторую строку на (-3/5) и прибавим к третьей, таки образом исключим переменную 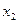 из третьей строки:
из третьей строки:
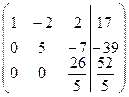 .
.
Получили систему уравнений, соответствующую последней матрице:
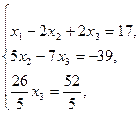
откуда, используя обратный ход метода Гаусса, найдем из третьего уравнения 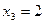 ; из второго уравнения найдем
; из второго уравнения найдем 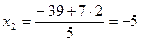 ; из первого уравнения
; из первого уравнения 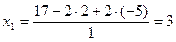 .
.
Ответ: (3; -5; 2).
Пример 7. Решить систему линейных уравнений методом Гаусса:
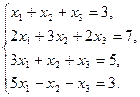
Дата публикования: 2015-09-17; Прочитано: 455 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
