Решение. Вычислим определитель системы

Вычислим определитель системы

.

Так как Δ ≠ 0, то решение системы может быть найдено по формулам Крамера (5). Для этого найдем :

.

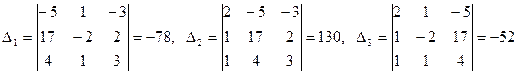Подставляя найденные значения определителей в формулы (5), получим искомое решение системы: .

Пример 5. Найти решение системы примера 4 с помощью обратной матрицы.

Решение.

Здесь

.

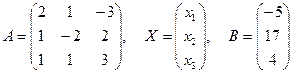Так как определитель матрицы системы отличен от нуля: |A|=-26, то матрица А имеет обратную. Для нахождения обратной матрицы вычислим алгебраические дополнения элементов матрицы . Транспонированная матрица имеет вид:

.

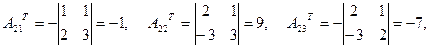
Согласно формуле (3), матрица , обратная к матрице А имеет вид

.

Проверим правильность вычисления , исходя из определения обратной матрицы (2) и используя формулу (1):

Матричное решение системы (8) в силу формулы (6) имеет вид

,

откуда следует (из условия равенства двух матриц), что .

Пример 6. Решить систему линейных уравнений методом Гаусса: