Решение. Рассмотрим минор первого порядка , следовательно, ранг матрицы

Рассмотрим минор первого порядка , следовательно, ранг матрицы .

Далее рассмотрим минор второго порядка: , т.к. минор второго порядка отличен от нуля, то . Найдем значение минора третьего порядка:

, следовательно, ранг матрицы равен 3, т.е. .

6. Алгоритм вычисления обратной матрицы:

1. Найти определитель исходной матрицы. Если = 0, то матрица А – вырожденная и обратная ей матрица не существует. Если , то матрица А – невырожденная и обратная матрица существует.

2. Найти матрицу 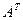, транспонированную к матрице А.

3. Найти алгебраические дополнения элементов транспонированной матрицы , , и составить из них присоединенную матрицу : , , .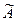

4. Вычислить обратную матрицу по формуле: .

5. Проверить правильность вычисления обратной матрицы , исходя из ее определения: .

Вычисление обратной матрицы методом Гаусса:

1) к матрице А приписать справа единичную матрицу Е той же размерности;

2) путем преобразований методом Гаусса над строками расширенной матрицы (А | E) матрица А приводится к единичной матрице;

3) в результате вычислительного процесса на месте приписанной справа матрицы Е получится обратная матрица .

Схематично процесс нахождения обратной матрицы выглядит следующим образом: (А | E) (E | ).

Пример 3. Найти обратную матрицу методом Гаусса для .