Основные положения. Классический метод расчета переходных процессов заключается в непосредственном интегрировании дифференциальных уравнений

Классический метод расчета переходных процессов заключается в непосредственном интегрировании дифференциальных уравнений, описывающих изменения токов и напряжений на участках цепи в переходном процессе.

В общем случае при использовании классического метода расчета составляются уравнения электромагнитного состояния цепи по законам Ома и Кирхгофа для мгновенных значений напряжений и токов, связанных между собой на отдельных элементах цепи соотношениями:

- резистор (идеальное активное сопротивление): ;

- катушка индуктивности (идеальная индуктивность): ;

- конденсатор (идеальная емкость): , .

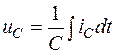Например, для последовательной цепи, содержащей линейные резистор r, катушку индуктивности L и конденсатор С (рис.1.6), при ее подключении к источнику ЭДС e по второму закону Кирхгофа имеем

или

. (1.1)

Подставив в (1.1) значение тока через конденсатор , получим линейное неоднородное дифференциальное уравнение второго порядка относительно :

.

В общем случае для цепи с n независимыми накопителями энергии уравнение, описывающее переходный процесс, имеет вид:

, (1.2)

где х – искомая функция времени (напряжение, ток, потокосцепление и т.п.); f (t) - известное возмущающее воздействие (напряжение и (или) ток источника электрической энергии); - k -й постоянный коэффициент, определяемый параметрами цепи.

Порядок данного уравнения равен числу независимых накопителей энергии в послекоммутационной цепи, под которыми понимаются катушки индуктивности и конденсаторы в упрощенной схеме, получаемой после объединения индуктивностей и соответственно емкостей элементов, соединенных последовательно или параллельно.

Наличие индуктивных связей на порядок дифференциального уравнения не влияет.

В зависимости от порядка дифференциальных уравнений, описывающих исследуемую цепь, различают цепи первого, второго и более высокого порядка.

Как известно из математики, общее решение неоднородного уравнения (1.2) представляет собой сумму частного решения исходного неоднородного уравнения и общего решения однородного уравнения, получаемого из исходного путем приравнивания его левой части к нулю.

Поскольку с математической стороны не накладывается каких-либо ограничений на выбор частного решения (1.2), применительно к электротехнике в качестве последнего удобно принять решение, соответствующее искомой величине х в установившемся послекоммутационном режиме (теоретически для t → ∞).

Частное решение уравнения (1.2) определяется видом функции f (t), стоящей в его правой части, и поэтому называется принужденной составляющей (обозначается х_пр).

Для цепей с заданными постоянными или периодическими напряжениями (токами) источников принужденная составляющая определяется из расчета установившегося режима работы цепи после коммутации любым методом расчета линейных электрических цепей. Например, при синусоидальном источнике питания рекомендуется использовать символический метод расчета.

Вторая составляющая общего решения х уравнения (1.2) – решение (1.2) с нулевой правой частью – соответствует режиму, когда внешние (принуждающие) силы (источники энергии) на цепь непосредственно не воздействуют. Влияние источников проявляется здесь через энергию, запасенную в полях катушек индуктивности и конденсаторов. Данный режим работы схемы называется свободным и описывается линейным однородным дифференциальным уравнением (1.3), общее решение которого называется свободной составляющей (обозначается х_св).

. (1.3)

В соответствии с вышесказанным, общее решение уравнения (1.2) имеет вид

х = х_пр + х_св. (1.4)

Соотношение (1.4) показывает, что в классическом методе расчета послекоммутационный режим рассматривается как наложение друг на друга двух режимов – принужденного, длящегося теоретически бесконечно долго, и свободного, имеющего место только в течение переходного процесса.

Поскольку принцип наложения справедлив только для линейных систем, метод решения, основанный на указанном разложении, справедлив только для линейных цепей.

В соответствии с определением свободной составляющей х_св в ее выражение входят постоянные интегрирования, число которых равно порядку дифференциального уравнения. Постоянные интегрирования находятся из начальных условий.

Выражение свободной составляющей определяется видом корней характеристического уравнения и зависит от значений параметров схемы (r, L, C) и схемы их соединений [1,2,3].

Зависимость вида свободной составляющей от вида корней характеристического уравнения приведена в табл.1.1.

Таблица 1.1

Вид корней характеристического уравнения	Выражение для свободной составляющей
Корни p 1, p 2, …, pn вещественные и различные
Корни p 1, p 2, …, pn вещественные и p 1= p 2= …= pm = p (m<n)
Пары комплексно-сопряженных корней pk,k+1= – δk ± jωk

Необходимо помнить, что, поскольку с течением времени свободная составляющая затухает, вещественные части корней характеристического уравнения не могут быть положительными.

При вещественных корнях х_св монотонно затухает, и имеет место апериодический переходный процесс. Наличие пары комплексно сопряженных корней обусловливает появление затухающих синусоидальных колебаний (колебательный переходный процесс).

Важной характеристикой при исследовании переходных процессов является постоянная времени τ, определяемая для цепей первого порядка, как:

,

где р – корень характеристического уравнения.

Постоянную времени можно интерпретировать как временной интервал, в течение которого свободная составляющая уменьшится в е раз по сравнению со своим начальным значением. Теоретически переходный процесс длится бесконечно долго, однако на практике считается, что он заканчивается при (3÷4) τ.