Цилиндрической поверхностью

В отличие от прямолинейчатых ци-линдрической и конической поверхнос-тей сферическая криволинейчата и от-личается тем, что фигура любого её плоского сечения является окружнос-тью. Поэтому образующие цилиндри-ческих поверхностей необходимо за-ключать в плоскости уровня, в которых окружности их сечения сферы изобра-жаются в натуральную величину.

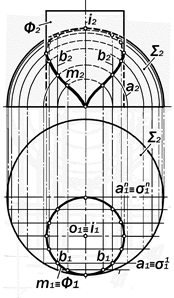
Рис.16.45. Графическое решение

позиционной задачи на пересечение сферы с поверхностью горизонтально-проецирующего цилиндра

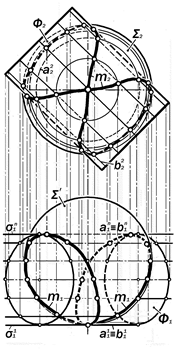
Рис.16.46. Графическое решение

позиционной задачи на пересечение сферы с поверхностью фронтально расположенного цилиндра

Пример 16.7. Построить двухкартин-ный комплексный чертёж пересекающихся поверхностей шара S и горизонтально-проецирующего цилиндра Ф (рис.16.45).

Анализ условия: 1.Так как пересекаю-щиеся поверхности являются кривыми, то линия их пересечения будет пространст-венной кривой;

2. Так как цилиндрическая поверхность Ф прямолинейчата, то точки встречи её об-разующих с сферой S будут точками иско-мой линии m их пересечения;

3.Так как поверхность Ф занимает в пространстве горизонтально-проецирую-щее положение, то её вырожденная в ли-нию горизонтальная проекция Ф₁, в силу собирательного свойства, содержит в себе горизонтальную проекцию m₁ искомой ли-нии m. Поэтому решение задачи сводится к построению фронтальной проекции m₂ этой линии путём графического моделирования отношения принадлежности точек линии m к поверхности шара S.

Решение: 1. Через необходимое и дос-таточное количество точек горизонтальной проекции m₁ линии m провести фронталь-ные параллели а₁¹ … а₁ⁿ;

2. Построить фронтальные проек-ции а₂¹ … а₂ⁿ этих параллелей в виде концентрических окружностей;

3. По точкам линии m₁ построить то-чки линии m₂ и соединить их плавной кри-вой линией.

Пример 16.8. Построить двухкартин-ный комплексный чертёж пересекающихся поверхностей шара S и фронтально рас-положенного цилиндра Ф (рис.16.46).

Анализ условия: Так как образующие цилиндрической поверхности Ф являются фронтальными линиями уровня, то их соот-ветственные пары определяют фронталь-ные плоскости s, пересекающие сферу S по её фронтальным параллелям а₁¹ … а₁ⁿ.

Поэтому поставленную задачу следует решать методом вспомогательных секущих плоскостей s, рассекающих поверхность S по окружностям а, а поверхность Ф – по её образующим b.

Решение: 1. В пределах горизонталь-ной проекции Ф₁ цилиндрической поверх-ности Ф провести горизонтально горизонта-льные следы s₁¹…s₁ⁿ ;

2. Построить фронтальные проекции а₁¹…а₁ⁿ линий пересечения s и S;

3. Построить фронтальные проекции b₂¹ …b₂ⁿ линий пересечения s и Ф;

4. Последовательно отметить точки пе-сечения фронтальных проекций компланар-ных линий а и b и соединить их плавной

кривой линией m₂ c учетом их видимости;

5.По фронтальной проекции m₂ линии m построить её горизонтальную проекцию m₁ на основе графического моделирования отношения принадлежности её точек как к поверхности Ф, так и к поверхности S.

Пример 16.9. Построить двухкартин-ный комплексный чертёж пересекающихся поверхностей шара S и цилиндра Ф обще-го положения (рис.16.47).

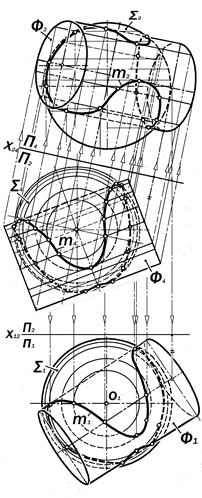
Рис. 16.47. Графическое решение позиционной задачи на пересечение сферы с поверхностью цилиндра общего положения

Анализ условия: Так как образующие поверхности цилиндра Ф занимают в про-странстве общее положение, то их можно заключать только в проецирующие плоско-сти, пересекающие сферу по окружностям, которые проецируются на П₁ и П₂ в эллип-сы. Для того, чтобы воспользоваться прое-кциями параллелей сферы в их натураль-ную величину, следует преобразовать дан-ный комплексный чертёж способом замены плоскостей проекций, расположив новую

фронтально-проецирующую плоскость про-

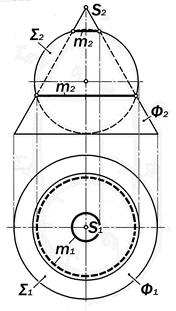
Рис.16.48. Графическое решение позиционной задачи на пересечение соосных сферы и поверхности конуса вращения

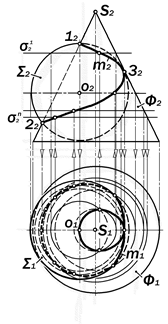
Рис.16.49. Графическое решение позиционной задачи на пересечение сферы и поверхности конуса вращения с фронтальной плоскостью симметрии

екций П₄ параллельно образующим цилин-дрической поверхности Ф. Проекция повер-хностей Ф и S на П₄ в паре с их проекцией на П₂ приводят к условию примера 16.8 (см. рис.16.46), решение которого приводит к построению фронтальной проекции m₂ ис-комой линии m. Её горизонтальная проек-ция m₁ строится на основе графического моделирования отношения принадлежно-сти её точек к поверхности сферы.

Решение: 1. Провести ось х₂₄ паралле-льно фронтальным проекциям образующих поверхности Ф;

2. Построить проекции Ф₄ и S₄ по зако-нам способа замены плоскостей проекций;

3. Построить проекции m₄ и m₂ по алго-ритму решения примера 16.8;

4. По m₂ построить m₁ моделируя отношение точек линии m к поверхности S.