Пересечение призматических и пирамидальных поверхностей

Общие замечания. Логика систем-ного исследования требует рассмотре-ния всех вариантов сочетания пересе-кающихся поверхностей, расположен-ных так или иначе в пространстве.

Анализ рис.16. 34 показывает, что

если одна или обе пересекающиеся призматические поверхности занимают проецирующие положения, то соответ-ственно одна или обе проекции иско-мой линии их пересечения, в силу соби-рательного свойства их вырожденных проекций, как бы содержатся в исход-ном условии. В случае необходимости следует графически промоделировать отношение принадлежности точек иско-мой линии к той поверхности, образу-ющие которой занимают в пространст-ве общее положение.

Анализ рис.16.35 показывает, что фигуры оснований поверхностей Ф и S

общего положения в пределах между крайними положениями горизонталь-ных следов s₁¹ и s₁ ⁿ вспомогательных

секущих плоскостей s являются косоу-гольными проекциями на П₁ искомой линии m по направлениям образующих

этих поверхностей (рис.16. 36). В этом случае получается, что фигуры основа-ний данных поверхностей в пределах их участков m₁¹ и m₁ⁿ также обладают собирательными свойствами, благода-ря чему полученный дважды косоуголь-ный комплексный чертёж линии m об-ладает свойством обратимости, позво-ляющим построить эту линию по её двум косоугольным проекциям.

Если пересекаются поверхности призмы Ф и пирамиды S, то фигура ли-нии m их пересечения, как принадле-жащая обеим поверхностям, будет про-ецироваться на плоскую фигуру осно-вания призмы Ф из центра S _Ф^¥, удален-ного по направлению её образующих в бесконечность, а на плоское основание пирамиды S – из её конечно располо-женной вершины S.

Так как обе поверхности прямоли-нейчаты, то параллельно-косоугольная проекция m ₁^Ф искомой линии m распо-ложится на линии основания поверх-ности Ф в пределах наложения на неё косоугольной проекции линейного кар-каса пирамиды S, а её центральная проекция m ₁ ^S совпадёт с фигурой осно-вания пирамиды S. Эти две проекции определяют обратным проецированием искомую линию m.

Пример 16.2.. Построить комплекс-ный чертёж пересекающихся призмати-ческой Ф и пирамидальной поверхности S с некомпланарными основаниями (рис. 16. 37).

Решение: 1. Построить проекции d₁, d₂ линии d пересечения оснований поверх-ностей Ф и S;

2. Спроецировать вершину S пирамиды

S по направлению рёбер призмы Ф на пло-скость её основания в точку К, a на плос-кость своего основания в точку L и изобра-зить их на комплексном чертеже;

3. Построить косоугольные проекции линейного каркаса пирамиды S на грани двугранного угла оснований данных повер-хностей. При этом проекции ребер пирами-ды, идущие в проекцию L вершины S, изла-мываются на ребре d и направляются в проекцию К вершины S на основание приз-мы Ф;

4. Точки пересечения проекций ребер пирамиды с фигурой основания призмы яв-

лются косоугольными проекциями искомых точек встречи ребер пирамиды с поверхно-стью призмы и наоборот, точки пересече-

ния проекций ребер призмы из вершины S

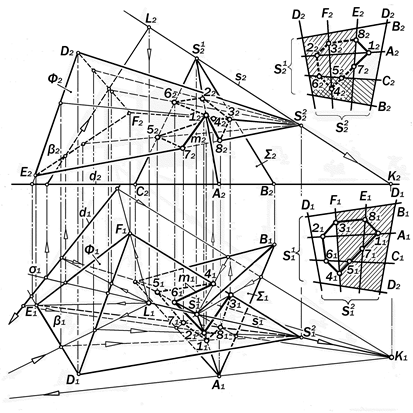
Рис.16.38. Графическое решение

позиционной задачи на пересечение двух пирамидальных поверхностей

на плоскость основания пирамиды с фигу-

рой этого основания являются централь-ными проекциями точек встречи рёбер при-змы с поверхностью пирамиды.

5. Построенные проекции вершин ис-комой пространственной ломаной линии m пересечения данных поверхностей соеди-нить между собой с учётом видимости, пользуясь способом условных разверток (см. рис.16.35).