Треугольников и их свойства

Процесс получения тени, падаю-щей от плоской фигуры на плоскость, является классическим примером прое-цирования этой фигуры световыми лу-чами, в результате которого устанавли-ваются коллинеарные соответствия ме-жду её элементами и элементами фигу-ры тени, конструктивное содержание которых описывается теоремой Дезар-га о двух гомологичных треугольниках (см. рис.6.12, 6.14).

ПРАВИЛО 34. Если плоская фигура параллельна одной из плоскостей про-екций, то фигура её действительной тени конгруэнтна данной фигуре, а фигура мнимой тени гомологична фи-гуре действительной тени в преобра-зовании сдвига относительно оси х₁₂ (рис. 13.28, а,б).

Рис13. 27 Иллюстрация правила 34

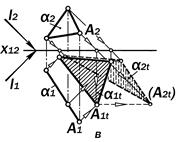
ПРАВИЛО 35. Если данная плоская фигура является проецирующей, то проекция тени, падающей от неё на плоскость проекций, к которой она не перпендикулярна, есть фигура, гомо-

логичная невырожденной проекции

данной фигуры, а фигура мнимой тени

соответственна фигуре действите-

льной тени в преобразовании сдвига относительно х₁₂ как оси гомологии

(рис.13. 28, а – г).

Рис. 13. 28. Иллюстрация правила 35

ПРАВИЛО 36. Если данная фигура занимает в пространстве общее по-ложение, то фигуры её действитель-ной и мнимой теней гомологичны фи-гурам их соответствующих ортого-нальных проекций при осях гомологий – их соответствующих следах h₁°, f₂°

(рис 13.30, 13.31).

Рис. 13.29. Иллюстрация правила 36

ПРАВИЛО 37. Если порядок чтения обозначений вершин той или иной про-екции плоской фигуры по или против часовой стрелки совпадает с поряд-ком чтения её одноименной тени, то такая проекция изображает освещен-ную сторону этой фигуры, а если этот порядок чтения нарушается, то соответствующая проекция фигуры изображает её обратную сторону, на-ходящуюся в собственной тени (см. рис.13.30, 13.31).

Рис. 13.30. Иллюстрация правил 37 и 38

ПРАВИЛО 38. Если плоская фигура отбрасывает тень на пересекающие-ся плоскости, то проекция фигуры па-

дающей тени изламывается на проек-

ции линии их пересечения (рис.13.31).

13.3.2. Проекции теней квадратов, прямоугольников и их свойства.

Для случаев, когда плоскости квад-

ратов или прямоугольников являются плоскостями уровня, справедливо пра-вило 34.

ПРАВИЛО 39. Фигура тени, падаю-щей на П₂ от горизонтального ква-драта со сторонами, параллельными и перпендикулярными к П₂, есть па-раллелограмм, равновеликий по пло-щади данному квадрату, так как он со-стоит из двух прямоугольных треуго-льников, которые конгруэнтны двум треугольникам, составляющим дан-ный квадрат (рис.13.32).

Рис.13.31. Иллюстрация правила 39.

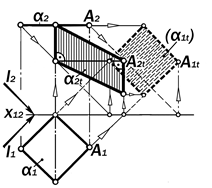
ПРАВИЛО 40. Фигура тени, падаю-щей на П₂ от горизонтального квадра-та со сторонами, расположенными к ней под 45° есть параллелограмм, со-стоящий из двух прямоугольных тре-угольников, гомологичных двум треу-гольникам, составляющий данный ква-драт (рис.13.33).

Рис.13.32. Иллюстрация правила 40

Рис. 13.33. Иллюстрации правила 41

Рис.13.34. Иллюстрация правила 42

. Рис. 13.35. Иллюстрация правила 43

ПРАВИЛО 41. Если стороны прое-цирующего квадрата расположены по отношению к той или иной плоскости проекций под углом 45°, а его плос-кость наклонена к неперпендикуляр-ной к ней плоскости проекций также под 45°, то фигура тени, падающей на ту плоскость проекций, к которой этот квадрат перпендикулярен, бу-дет ромбом (рис.13. 34, а,б).

ПРАВИЛО 42. Если фигура квадра-та a занимает такое общее поло-жение в пространстве, при котором её горизонтальный след h₁° перпенди-кулярен к горизонтальной проекции l₁ светового луча l, а её плоскость сим-метрична плоскости П₁ относитель-но плоскости d, перпендикулярной световым лучам, то фигурой его па-дающей на П₁ тени будет конгруэнт-ный ему квадрат (рис. 13.34).

Очевидно, что это правило спра-

ведливо не только для крадрата, но и для любой плоской фигуры, именно так расположенной в пространстве.

Получается, что фигура падаю-

щей тени конгруэнтна освещаемой фи-гуре не только тогда когда их плоско-сти параллельны.

ПРАВИЛО 43. Если наклонные сле-ды проецирующих плоскостей пря-моугольников, стороны которых явля-ются линиями их уровня и наиболь-шего уклона, расположены перпенди-клярно к одноименным проекциям све-тового луча, то на одной плоскости проекций фигурой тени данного пря-моугольника будет прямоугольник, а на второй, - параллелограмм как резу-льтат преобразования сдвига этого прямоугольника (рис. 13. 35, а, б).

ПРАВИЛО 44. Если наклонные сле-ды проецирующих плоскостей прямо-угольников параллельны одноимен-ным проекциям светового луча, то, независимо от расположения их сто-рон по отношению к плоскостям про-екций, их падающие тени совпадают с их соответствующими следами. (рис. 13.36, а, б).

Вполне очевидно, что это правило справедливо не только для прямоуголь-

ников, но и для любых других плоских

фигур иной конфигурации.

Рис.13.36. Иллюстрации правила 44

ПРАВИЛО 45. Если проекции парал-лельных строн произвольного прямо-угольника или параллелограмма па-раллельны одноименным проекциям светового луча, то его действитель-ная и мнимая тени представляют собой прямые линии (рис. 13.37).

Рис13.37. Иллюстрация правила 45.