Игровой подход к принятию решений в условиях неопределённости

Достаточно часто решения приходится принимать в условиях неопределенности, когда или про­цесс выполнения операции является неопределенным, или нам со­знательно противодействует противник, или нет ясных и четких целей (задач) операции. Следствием неопределенности является то, что успех операции зависит не только от наших решений, но и от чьих-то решений или действий.

В целом ряде задач приходится анализировать ситуации, в ко­торых сталкиваются какие-то противоборствующие стороны (две или более), каждая из которых преследует свою цель, причем ре­зультат любого мероприятия каждой из сторон зависит от того, какие действия предпримет противник. Столкновение противоположных интересов участников приводит к возникновению конфликтных ситуаций. Необходимость анализировать такие ситуации, в свою очередь, привела к возникновению теории игр, задачей которой является выработка рекомендаций по рациональному образу действия участников конфликта. Теорию игр можно определить как теорию математических моделей при­нятия решений в условиях конфликта. Теория игр – это теория математических моделей, интересы участников которых различны.

Чтобы исключить трудности, возникающие при анализе практических конфликтных ситуаций в результате наличия многих несущественных факторов, строится упрощённая модель ситуации. Такая модель называется игрой. Конфликтная ситуация в игровой модели развивается по определённым правилам (обратите внимание на то, что крайний экстремизм: «На­рушать любое правило» является правилом). Естественным примером конфликтных ситуаций служат широко распространённые игры – шахматы, шашки, карточные игры. Поэтому теории игр свойственна следующая терминология: «игроки» (стороны, участвующие в конфликте), «выигрыш» (исход конфликта) и т.д.

Среди задач, требующих применения теории игр, можно на­звать следующие:

- анализ конфликтных ситуаций в экономике (простым экономическим примером конфликтной ситуа­ции, для описания которой применяется теория игр, является кон­курентная борьба торговых фирм или промышленных предприя­тий);

- обменные и торговые операции;

- анализ и проектирование иерархических структур управле­ния и экономических механизмов (например, анализ различных моделей стимулирования);

- анализ коалиционного поведения.

Теория игр предназначена для получения решений в играх, ко­торые играются только один раз. Если игра повторяется, то надо использовать статистические методы. В единичной, неповторяющейся игре теория игр либо позволяет выбрать одно определенное “хорошее” в том или ином смысле решение из множества возможных решений, либо по­лучить характеристики того случайного механизма, с помощью которого один раз выбирается какое-то одно из возможных решений.

3.2. Основные понятия теории игр.

Обычно, достижение цели сопровождается каким-то выигры­шем, который является своего рода мерой эффективности. Конеч­но, при разных решениях участников могут быть разные величи­ны выигрышей. Если участников двое, то совокупность всех выиг­рышей можно представить в виде таблицы — матрицы выигры­шей или платежной матрицы, которая определяет, какой платеж должен быть сделан одним участником другому. Игра двух лиц с нулевой суммой — это такая игра, в которой сумма выигры­шей участников после конца игры равна нулю (сколько один выиграл, столько другой проиграл).

Важным понятием теории игр яв­ляется понятие стратегии. Стратегия,— это установленный игро­ком метод выбора ходов в течение игры. Можно понимать страте­гию как план проведения игры, причем этот план настолько ис­черпывающий, что он не может быть нарушен действиями про­тивника.

Суммируя все сказанное, можно сказать, что матричная игра с нулевой суммой двух лиц, у каждого из которых имеется конеч­ное множество стратегий, представляется в виде матрицы выигры­шей одного из игроков (выигрыши другого противоположны по знаку), которые являются элементами матрицы и показывают, что получает этот игрок при каждой комбинации какой-то своей стра­тегии и какой-то стратегии противника. Обычно считается, что строки матрицы соответствуют стратегиям первого игрока, столб­цы — стратегия второго, первый выбирает строку, второй — столбец, на пересечении стоит выигрыш первого игрока (возможно, что он отрицателен, то есть первый игрок в проигрыше). Если раз­мерность матрицы , то игра называется игрой , то есть размерность игры определяется числом стратегий. Матричные иг­ры — не единственный тип игр, но мы займемся иг­рами этого типа.

Рассмотрим пример.

Пример 3.1. Пусть двое игроков, одновременно и не зная выбора против­ника, кладут на стол по монете. При совпадении сторон обе мо­неты забирает первый игрок, при несовпадении обе монеты заби­рает второй игрок У каждого из игроков по две стратегии {Г, Р} и {Г, Р}. Число возможных ситуаций — четыре. Пусть выигрыш первого игрока (+1), его проигрыш (-1). Тогда матрица игры имеет вид:

,

где слева выписаны стратегии первого игрока, над матрицей — стратегии второго.

Надо отметить важную терминологическую деталь: стратегии, указываемые в приведенных примерах слева от платежной матри­цы и над ней, называются чистыми, каждый игрок применяет в игре только одну из своих возможных стратегий.

Теперь, используя понятие чистой стратегии, рассмотрим сле­дующую ситуацию [2]. На один и тот же рынок первая фирма A может поставлять какие-то три своих продукта А1, А2,А3, вторая - B— че­тыре продукта B1, B2, B3, B4. В силу некоторых обстоятельств, в частности из-за нежелания устраивать конкуренцию между соб­ственными продуктами, каждая из фирм собирается поставлять на данный рынок только какой-то один из своих продуктов. Пла­тежная матрица для первой фирмы имеет вид:

.

Элемент aij матрицы — размер выигрыша 1-ой фирмы, если она поставляет на рынок продукт Ai, а вторая фирма – продукт Bj.

Принятие решений каждой фирмой о том, какой продукт по­ставлять на данный рынок, и есть выбор определенной чистой стратегии. Ясно, что первой фирме хотелось бы поставлять на ры­нок продукт A1, но она опасается, что вторая фирма поставит про­дукт B1 и тогда вместо выигрыша в 20 единиц фирме грозит про­игрыш в 5 единиц. Ясно, что вторая фирма хотела бы поставлять на рынок либо B1, либо B4,так как при этом первая фирма имела бы максимальный проигрыш, что означает максимальный выиг­рыш второй фирмы. Но для второй фирмы очевидна рискован­ность этих решений: B1 или B4, встретившись на рынке с продук­том A1 или A2 первой фирмы (который дает этой фирме выигрыш в 20 или 18 единиц), принесут второй фирме 20 или 18 единиц убытков. Даже в ситуации, когда вторая фирма только осваивает новый рынок, она, естественно, хочет иметь эти потери поменьше.

Представляется логичным следующее осторожное поведение каждой из фирм. Первая фирма смотрит, какой минимальный вы­игрыш она получает при каждой из своих стратегий: A1 дает (-5), A2 дает (0), A3 дает (-5). Выбрав стратегию A2 (она дает макси­мальный выигрыш среди минимально возможных), первая фирма получает не меньше чем (0). Более того, если вторая фирма выбе­рет, например, четвертую стратегию, то первая выиграет (+6). Ви­дим, что осторожное поведение для первой фирмы диктует ей та­кое поведение: среди выигрышей aij в каждой строке найти выиг­рыш ai = , а затем выбрать стратегию с таким номером i, для которого выигрыш ai максимален 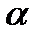= . Окончательно получается, что при разумной осторожности 1-ая фирма может получить не меньше 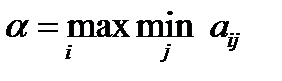. Величина 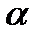- гарантированный выигрыш первого игрока, называется нижней ценой игры. Стратегия Ai0, обеспечиваю­щая получение 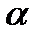, называется максиминной.

Поскольку платежная матрица выписана как матрица выигрышей первой фирмы, постольку вто­рая фирма, действуя с разумной осторожностью, будет рассуж­дать так. В каждом столбце (она ведь «контролирует» столбцы, выбирая, какой товар отправить на рынок) определяется максималь­ный проигрыш этой фирмы, то есть максимальный выигрыш пер­вой фирмы, bj = 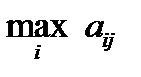, потом выбирается тот столбец, то есть та стратегия, для которой = 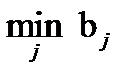. В этом случае вторая фирма потеряет не больше чем . Величина называется верхней ценой игры, а соответствующая выигрышу стратегия Bj0 — минимаксной.

Достаточно просто доказывается, что всегда

= <= =

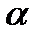В самом деле, пусть ars= , aqp= .

Ясно, что ars — минимальный элемент r-ой строки, значит, ars <= arp, элемент aqp — максимален в р-ом столбце, поэтому arp<= aqp, следовательно, ars<= arp<= aqp, что и требовалось дока­зать.

Фактический выигрыш игрока А при разумных дейст­виях партнеров ограничен нижней и верхней ценой игры. Если же эти выражения равны, т. е.

= =v,

то выигрыш игрока А — вполне определенное число, игра называется вполне определенной, а выигрыш v называет­ся значением игры или ценой игры и равен элементу матрицы ai0j0. Вполне определенные игры называют играми с седловой точ­кой. Элемент ai0j0 в матрице такой игры является одновре­менно минимальным в строке i0, максимальным в столбце j0 и называется седловой точкой. Седловой точке соответ­ствуют оптимальные стратегии игроков, их совокупность является решением игры, которое обладает следующим свой­ством: если один из игроков придерживается своей опти­мальной стратегии, то для другого отклонение от его опти­мальной стратегии не может быть выгодно.

Седловая точка может быть не единственной, но при этом значение aij во всех седловых точках будет одним и тем же, равным цене игры v.

Пример 3.2. Определить нижнюю и верхнюю цены для игр, заданных платежными матрицами A1 и А2:

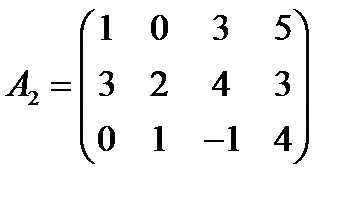
Решение. Минимальные значения aij в строках мат­рицы А1 равны соответственно 2, 3, 1. Максимальное значе­ние из них равно 3. Следовательно, — нижняя цена игры, которой соответствует матрица A1, равна 3.

Для определения (верхней цены данной игры) найдем максимальные значения элементов в столбцах матрицы. По столбцам соответственно имеем: 4, 5, 6, 5. Следовательно, = 4. Для матрицы А2

,

.

Таким образом, = = v — цена игры. Решение дан­ной игры состоит в выборе игроком А стратегии А2, при этом его выигрыш не меньше 2; для игрока В оптимальной является стратегия В2, позволяющая ограничить его про­игрыш этим же числом. Легко видеть, что отклонение одним из игроков от оптимальной стратегии приводит к уменьше­нию выигрыша (для игрока А) и увеличению проигрыша (для игрока В).

Итак, если игровая матрица содержит седловую точку, то решение игры известно. Каждый из игроков применяет свою оптимальную стратегию. Возникает вопрос нахождения ре­шения для игр, матрицы которых не содержат седловой точ­ки. В этих играх . Применение минимаксных страте­гий для каждого из игроков обеспечивает выигрыш, не превышающий , и проигрыш, не меньший . Естествен­ным для каждого игрока является вопрос увеличения вы­игрыша (уменьшения проигрыша). Поиски такого решения состоят в том, что игроки применяют не одну, а несколько стратегий. Выбор стратегий осуществляется случайным образом. Случайный выбор игроком своих стратегий называется смешанной стратегией.

В игре, матрица которой имеет размерность , стра­тегии игрока А задаются наборами вероятностей X = (х1, х2,…,хm), с которыми игрок применяет свои чистые стратегии. Эти наборы можно рассматривать как m-мерные векторы, для компонент которых выполняются условия

Аналогично, для игрока В определяют n-мерные векторы Y = (y1,y2,…,yn), соответствующие его смешанным стра­тегиям. Стратегии игроков А и В, для которых вероятности xi и yj отличны от нуля, называются активными.

Согласно основной теореме теории игр, каждая конечная игра имеет по крайней мере одно решение, которым может быть и определенная смешанная стратегия. Выигрыш игрока А при использовании смешанных стратегий определяется как математическое ожидание выигрыша, т.е. 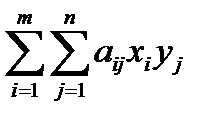или (в векторной записи) XAY'. Применение оптимальной стратегии позволяет получить выигрыш, равный цене игры [3]

.

Для оптимальных стратегий игроков имеет место соот­ношение

.

Применение игроком А оптимальной стратегии X* должно обеспечивать ему при любых действиях игрока В выигрыш не меньше цены игры v. Поэтому выполняются следующие соотношения:

(3.1)

Аналогично, для игрока В оптимальная стратегия Y* долж­на обеспечить при любых стратегиях игрока А проигрыш, не превышающий величину v, т. е. справедливо соотноше­ние

(3.2)

Доминирование стратегий. Если платежная матрица такова, что каждый элемент некоторой строки i не меньше соответствующе­го элемента строки к и по меньшей мере один ее элемент строго больше соответствующего элемента строки к, то говорят, что стра­тегия Aj игрока 1 доминирует его стратегию Ak. Доминируемая стра­тегия не может быть оптимальной чистой стратегией игрока 1 и даже не может войти в его оптимальную смешанную стратегию с ненулевой вероятностью, поэтому ее можно исключить из рас­смотрения, вычеркнув из матрицы строку к. Аналогично: если каждый элемент некоторого столбца j не больше соответству­ющего элемента столбца r и по меньшей мере один его элемент строго меньше соответствующего элемента столбца r, то гово­рят, что стратегия Bj игрока 2 доминирует его стратегию Br. Поэтому столбец r матрицы можно вычеркнуть.

Пример 3.3 [2]. Рассмотрим пример использования теории игр при решении экономической задачи, которая может возникнуть в практике менеджера.

Предположим, есть две фирмы А и В, торгующие одним и тем же товаром, который пользуется спросом в течение N единиц времени. Пусть c — доход от продажи товара в едини­цу времени, причем продажа товара по заниженной цене законо­дательно запрещена. Далее, пусть качество товара зависит от вре­мени поступления на рынок: чем позже товар поступает на ры­нок, тем качество выше, причем реализуется только товар более высокого качества. Наконец, пусть фирма В хочет разорить фир­му А, не заботясь о своих доходах. Фирма В может использовать в качестве законного средства только момент поступления своего товара на рынок. Пусть i — момент поступления товара на ры­нок от фирмы А, j — момент поступления товара от фирмы В, выбор моментов — единственно возможные управленческие ре­шения, фирма А хочет максимизировать свой доход, фирма В, как уже сказано, хочет минимизировать доход фирмы А.

Найдем функцию выигрыша, то есть доход фирмы А. Если А выпустит товар в момент i, а В — в момент j > i (скажем, i = 2, j= 5), то А не будет иметь конкурентов в течение j - i единиц времени и получит за это время доход с (j – i). Начиная с момен­та j, на рынке будет более «свежий» товар фирмы В, поэтому с момента j фирма А теряет свой доход. Если j < i, то есть фирма В раньше А выбрасывает на рынок свой товар; то доход фирмы А будет равен c (n + 1 - i). Если, наконец, i =j, то товары обеих фирм имеют одинаковый спрос, и каждая из фирм получает до­ход с (п + 1 - i)/2. Получаем функцию выигрыша фирмы А (она же функция проигрыша В):

Пусть, например, п = 4. Тогда платежная матрица игры имеет вид:

Даже без строгих доказательств, на уровне здраво­го смысла, видно, что величину c в записи матрицы можно опус­тить.

Во-вторых, размерность матрицы можно уменьшить, удалив доминируемые стратегии: для фир­мы В, контролирующей столбцы, первый столбец заведомо хуже второго, так как первая стратегия этой фирмы несет ей больший проигрыш, чем вторая. Фирма В свою первую стратегию исполь­зовать не будет (эта стратегия — доминируемая), поэтому можно перейти к матрице:

.

Фирма А не станет использовать свою четвертую стратегию, так как при выборе этой фирмой третьей стратегии ее выигрыш может быть лишь больше или равен выигрышу, соответствующе­му четвертой стратегии.

Поэтому можно перейти к матрице:

Теперь видим, что фирме В не стоит использовать третью из оставшихся стратегий, так как она доминируется второй, при вы­боре которой проигрыш этой фирмы меньше.

Поэтому переходим к матрице:

.

Наконец, видим, что фирма А не станет использовать свою вто­рую из оставшихся стратегий, так как выигрыш по ней меньше, чем по третьей. В итоге получаем матрицу:

которая не имеет седловой точки, то есть решение надо искать не в чистых, а в смешанных стратегиях.

Для последней матрицы оптимальные вероятности мож­но найти, например, графически и получить для А: X*= (0,5; 0,5), для В: Y*= (0,5; 0,5), что дает для исходной матрицы (с учетом отбрасывания второй и четвертой стратегии для А и первой и чет­вертой стратегии для В): X*= (0,5; 0; 0,5; 0), Y* = (0; 0,5; 0,5; 0). Цена игры (выигрыш, доход А или проигрыш В):

то есть, возвращаясь к истинной стоимости, v=1.5c. Смысл полу­ченного результата ясен: фирма А должна с равными вероятнос­тями выпускать товар в 1-й или 3-й момент, а фирма В — во 2-й или 3-й. При этом ожидаемый выигрыш А равен 1,5с (разорит ли А такой уровень дохода, это уже другой вопрос).

3.3. Сведения матричной игры к задаче линейного программирования [2, 3]

Если седловая точка отсутствует, то общим методом решения игры любой (конечной) размерности является сведение игры двух лиц с нулевой суммой к задаче линейного программирования. Из основного положения теории стратегических игр следует, что при использовании смешанных стратегий существует по меньшей мере одно оптимальное решение с ценой игры v, причем, , т.е. цена игры находится между ниж­ним и верхним значениями игры. Величина v неизвестна, но мож­но предположить, что v > 0. Это условие выполняется, поскольку путем преобразования матрицы всегда можно сделать все ее эле­менты положительными. Таким образом, если в исходной платеж­ной матрице имеется хотя бы один неположительный элемент, то первым шагом в процедуре сведения игры к задаче линейного программирования должно быть ее преобразование в матрицу, все элементы которой строго положительны. Для этого достаточно увеличить все элементы исходной матрицы на одно и то же число , где . При таком преобразовании мат­рицы оптимальные стратегии игроков не изменяются.

Допустим, что смешанная стратегия игрока 1 складывается из стратегий A1,A2,…,Am с вероятностями соответственно х1, х2,…,хm (). Оптимальная смешанная стратегия игрока 2 скла­дывается из стратегий B1, B2,…,Bn с вероятностями y1,y2,…,yn

Условия игры определяются платежной матрицей

.

Если игрок 1 применяет оптимальную смешанную стратегию, а игрок 2 — чистую стратегию Bj, то средний выигрыш игрока 1 (математическое ожидание выигрыша) составит х1a1j + х2a2j+…+xmamj, j=1,…,n.

Игрок 1 стремится к тому, чтобы при любой стратегии игрока 2 его выигрыш был не менее чем цена игры v (смотри (3.1)) и сама цена игры была максимальной. Такое поведение игрока 1 описывается следующей моделью линейного программирования:

(игрок 1 стремится максимизировать свой выигрыш),

х1a11 + х2a21+…+xmaь1 v

х1a12 + х2a22+…+xmam2 v

х1a1n + х2a2n+…+xmamn v,

Преобразуем систему ограничений, разделив все члены неравенств на v (v >0) и обозначим ti =xi. Из условия х1 + х2+…+xm =1 следует, что t1 + t2+…+tm =1/v. В результате получаем следующую задачу линейного программирования:

t1 + t2+…+tm min

t1a11 + t2a21+…+tmaь1 1

t1a12 + t2a22+…+tmam2 1 (3.3)

t1a1n + t2a2n+…+tmamn 1

ti 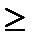0, i=1,…,m.

Поведению игрока 2 соответствует двойственная задача:

u1 + u2+…+un max (эквивалентно v min: игрок 2 стремится минимизироиать свой средний проигрыш)

a11u1+a12u2+…+a1nun 1

a21u1+a22u2+…+a2nun 1 (3.4)

am1u1+am2u2+…+amnun 1,

где uj 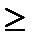0, j=1,…,n

Таким образом, для решения игры имеем пару симметричных двойст­венных задач линейного программирования. Используя свойство симметричности, можно решить одну из них, а решение второй задачи найти на основании оптимального плана двойствен­ной к ней задачи.

Задача (3.3) всегда имеет решение. Получив ее оптимальное решение t1*, t2*,…, tm*, можно найти цену игры v*=1/(t1*+ t2*+…+ tm), оптимальные значения x1*, x2*,…, xm (xi*= ti*v*) и, следовательно, оптималь­ную стратегию игрока 1. Оптималь­ную стратегию игрока 2 находим по формуле yi*= ui*v*.

Если исходная матрица увеличивалась на d, то для получения цены первоначальной игры v* нужно умень­шить на d.

3.4. Матричная игра двух лиц с ненулевой постоянной суммой [1]

Конечная игра, в которой сумма выигрышей обоих игроков не равна нулю и постоянна для всех сочетаний их чистых стратегий, называется матричной игрой двух лиц с ненулевой постоянной сум­мой. Пусть — матрица выигрышей игрока 1 и — матрица выигрышей игрока 2. Причем aij +bij =c для всех i=1,…,m; j=1,…,n.

Такого рода игра сводится к игре двух лиц с нулевой суммой следующим образом:

каждому игроку выплачивается сумма с/2;

решается игра с нулевой суммой с матрицей выигрышей

игрока 1, где .

Действительно, в игре с преобразованной таким способом мат­рицей выигрышей игрок 2 получает сумму для всех i = 1,..., т; j = 1,..., п, т.е. новая игра является игрой с нулевой суммой. При этом каждый игрок ничего не теряет от того, что каждый из них в игре получает на с/2 меньше, поскольку по с/2 они получили перед игрой.

Примеры

Пример 1[1]. Выбор стратегии. Матрица некоторой игры имеет вид

B A	B1	B2	B3	B4	Минимальный выигрыш игрока 1
A1
A2
A3
Максимальный проигрыш игрока 2

Найдите оптимальные стратегии игроков.

Решение. В этой игре игрок 1 имеет три возможные страте­гии: A1, A2, A3, а игрок 2 — четыре возможные стратегии: B1, B2, B3, B4.

Рассмотрим процесс принятия игроками решения (предпола­гается, что они действуют рационально). Взглянув на таблицу, можно заметить, что если игрок 1 не знает, как поступит его про­тивник, то, действуя наиболее целесообразно и считая, что про­тивник будет действовать подобным же образом, он выберет стра­тегию A2, которая гарантирует ему наибольший из трех возмож­ных наименьших выигрышей: 9, 13, 8. Другими словами, игрок 1 руководствуется принципом максиминного выигрыша. Эгот выигрыш 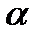= есть нижняя цена игры. Для нашего примера 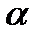= 13.

Игрок 2 рассуждает аналогично: если он выберет стратегию B1, то потеряет самое большее 23, если стратегию B2, то — 40, и т.д. В результате он выберет стратегию B3, которая гарантирует ему наименьший из четырех возможных проигрышей: 23, 40, 13, 25. Принято говорить. что игрок 2 руководствуется принципом мини­максного проигрыша. Этот проигрыш есть верхняя цена игры. Для нашей матрицы = 13.

Ситуация (A2, B3) есть седловая точка и 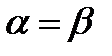= 13 есть цена игры.

При наличии седловой точки ни одному из участников игры невыгодно отклоняться от своей минимаксной стратегии: он бу­дет наказан противником тем, что получит меньший выигрыш.

Пример 2[1]. Где строить?

Две конкурирующие крупные торговые фирмы Ф1 и Ф2 пла­нируют построить в одном из четырех небольших городов Г1, Г2, Г3 и Г4, лежащих вдоль автомагистрали, по одному универсаму. Взаимное расположение городов, расстояние между ними и чис­ленность населения показаны на рис.3.1.

Чис­ленность населения (тыс. чел.): Г1 – 30; Г2 – 50; Г3 – 40; Г4 - 30

рис.3.1

Прибыль каждой фирмы зависит от численности населения городов и степени удаленности универсамов от места жительства потенциальных покупателей. Специально проведенное исследова­ние показало, что прибыль в универсамах будет распределяться между фирмами следующим образом:

Универсам фирмы Ф1 по сравнению с универсамом фирмы Ф2 расположен от города	Распределение прибыли между фирмами
Ф1	Ф2
Ближе	75%	25%
На одинаковом расстоянии	60%	40%
Дальше	45%	55%

Например, если универсам фирмы Ф1 расположен к городу Г1 ближе универсама фирмы Ф2, то прибыль от покупок, сделанных жителями данного города, распределится следующим образом: 75% получит Ф1, остальное — Ф2.

Представьте описанную ситуацию как игру двух лиц.

В каких городах фирмам целесообразно построить свои уни­версамы?

Решение. Составим платежную матрицу игры, в которой иг­роком 1 будет фирма Ф1, а игроком 2 — фирма Ф2. Стратегии обо­их игроков: строить свой универсам в городе Г1, в городе Г2 и т.д. Элементы матрицы — прибыль фирмы Ф1 (в тыс. руб.), которая, как предполагается, пропорциональна (причем с одним и тем же коэффициентом) числу покупателей. Величина указанного коэф­фициента пропорциональности для выбора оптимального места размещения универсамов значения не имеет, поэтому примем его равным единице.

Ф2 Ф1	Г1	Г2	Г3	Г4
Г1		76,5	91,5	91,5
Г2	103,5		91,5	103,5
Г3	88,5	88,5		103,5
Г4	88,5	76,5	76,5

Платежная матрица имеет вид

Рассмотрим примеры расчета значений элементов (Г1, Г2) и (Г3, Г4) матрицы.

Ситуация (Г1, Г2) означает, что фирма Ф1 строит универсам в городе Г1, а фирма Ф2— в городе Г2. Число покупателей фирмы Ф1 складывается из покупателей четырех городов. Для ситуации (Г1, Г2) число покупателей из Г1: 0,75 30, из Г2: 0,45 50, из Г3: 0,45 40, из Г4: 0,45 30, т.е. в сумме 76,5 тыс. руб. Для ситуации (Г3, Г4) число покупателей из Г1: 0,75 30, из Г2: 0,75 50, из Г3: 0,75 40, из Г4:0,45-30, т.е. в сумме 103,5 тыс. руб. Элементы мат­рицы выигрышей фирмы Ф2 — дополнения до числа 150 (общее число жителей в четырех городах). Таким образом, имеет место игра двух лиц с ненулевой постоянной суммой, оптимальные стратегии которой те же, что и для соответствующей игры с ну­левой суммой.

Полученная платежная матрица имеет седловую точку (Г2, Г2). Соответствующий элемент матрицы равен 90.

Таким образом, обеим фирмам следует строить свои универ­самы в одном и том же городе Г2, при этом прибыль фирмы Фх составит 90 тыс., а фирмы Ф2 — 60 тыс. руб.

Пример 3[2]. Магазин может завезти товар п типов (i = 1,..., п, i — номер типа товара). Если товар будет пользоваться спросом, то прибыль от его реализации будет рi, если товар не будет поль­зоваться спросом, то убыток составит li. Прогноз спроса отсутст­вует. Первый игрок — магазин, второй — покупательский спрос, который играет роль «природного фактора», а не разумного про­тивника. Товары считаются такими, что спрос на один из них оз­начает отсутствие спроса на другие.

Платежная матрица имеет вид:

При отсутствии прогноза спроса гарантированный для магази­на результат получается при ориентации на наихудший спрос. Пусть, например, известна следующая исходная информация:

Тип товара	Доход	Убыток

Платежная матрица

.

Решение этой игры получаем, решив соответствующую ЗЛП для игрока 1: X* = (0,16; 0,19; 0,21; 0,21; 0,23). Магазин должен пользоваться смешанной стратегией с частотами X* = (0,16; 0,19; 0,21; 0,21; 0,23), его ожидаемый выигрыш v = 1,4. Смысл этого результата в том, что магазину целесообразно закупить товар всех типов в пропор­циях: 16% — 1-го типа, 19% — 2-го типа, 21% — 3-го типа, 21% — 4-го типа и 23% — 5-го типа. Согласитесь, что «здравый смысл» рекомендует завезти товар 5-го типа «побольше» и не завозить товар 1-го типа вовсе.

Пример 4[1]. Двухпальцевая «игра морра».

Каждый игрок показывает один или два пальца и называет число пальцев, которое, по его мнению, показал его противник (ни один из игроков не видит, какое число пальцев на самом деле показывает его противник). Если один из игроков угадывает правильно, он выигрывает сумму, равную сумме числа пальцев, по­казанных им и его противником. В противном случае (если ни­кто не угадывает)— ничья. Если оба угадали, то игроки платят друг другу одинаковую сумму, в результате также ничья.

Вопросы:

Существует ли в данной игре седловая точка?

Кто из игроков в среднем выигрывает и сколько?

Как часто игрок 1 должен говорить, что его противник по­
казал два пальца?

Как часто игрок 2 должен показывать один палец?

Решение. Прежде всего определим стратегии игроков и по­строим платежную матрицу.

Стратегиями игрока 1 (строки таблицы) являются четыре пары чисел. Первое число каждой пары — это число пальцев, показан­ное им, второе — число пальцев, которое, как он предполагает, показал его противник. Такие же стратегии имеет игрок 2.

Платежная матрица размером 4 х 4 и другая информация пред­ставлены в следующей таблице:

Игрок 2   Игрок1	(1,1)	(1,2)	(2,1)	(2,2)	Минимальный выигрыш игрока 1
(1, 1)			-3		-3
(1, 2)	-2				-2
(2,1)				-4,	-4
(2,2)		_2			-3
Максимальный проигрыш игрока 2

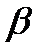Нижняя цена игры =-2, верхняя цена игры = 2.

Как видим, , поэтому седловой точки не существует и ре­шение в чистых стратегиях отсутствует. Для решения данной игры построим соответствующую задачу линейного программирования. Для этого сначала преобразуем платежную матрицу таким обра­зом, чтобы все ее элементы были положительными. Максималь­ное по абсолютной величине значение неположительного элемента платежной матрицы равно 4, поэтому к матрице достаточно при­бавить число 5:

Игрок 2   Игрок1	(1,1)	(1,2)	(2,1)	(2,2)	Минимальный выигрыш игрока 1
(1, 1)
(1, 2)
(2,1)
(2,2)
Максимальный проигрыш игрока 2

Оптимальная стратегия игрока 1 находится решением следу­ющей задачи линейного программирования:

t1 + t2+t3+ t4 min

5t1 +3t2+8t3 +5t4 1

7t1 +5 t2+5t3 +2t4 1

2t1 +5t2+5t3 +9t4 1

5t1 +8t2+1t3 +5t4 1

ti 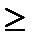0, i=1,…,4.

Используя надстройку EXCEL Поиск решения, получаем решение задачи линейного программирования t1*=0, t2*=0,1143, t3*=0, t4*=0,0857.

Оптимальное значение целевой функции равно 0,2. Решение двойственной задачи имеет вид u1*=0, u2*=0,1143, u3*= 0,0857 u4*= 0. Переходя к переменным исходной задачи и учитывая, что цена игры v равна v = 1/(t1* + t2*+t3*+ t4*) = 5 и вероятность xi i-ой чистой стратегии равна xi = ti* v, получаем:

x1 = 0, x2 = 0,5715, x3 = 0, x4 = 0,4285.

Это означает, что при многократном повторении игры первая стратегия (1,1) и третья стратегия (2,1) игроком 1 не должны ис­пользоваться; вторая стратегия (1,2) должна использоваться с ча­стотой 0,5715, четвертая стратегия (2, 2) — с частотой 0,4285.

Аналогично определяем оптимальную стратегию игрока 2:

y1 =0, y2 = 0,1143 5= 0,5715, y3=0,0857 5=0,4285, y4 = 0,

т.е. игрок 2 должен использовать лишь свою вторую стратегию (1,2) с частотой 0,5715 и третью стратегию (2, 1) с частотой 0,4285.

Так как исходная матрица была увеличена на 5, получаем, что цена первоначальной игры равна 0 (5 – 5=0). Таким образом, исход игры — ничья.

Ответы: 1. Нет, не существует. 2. Ничья.

3. Всегда. 4. 0,572.

Пример 5[1]. Доминирование стратегий.

Платежная матрица для двух игроков имеет вид

Стратегии игрока2 г   Стратегии игрока 1
			-8
			-8
					-1
	-2

Преобразуйте игру, исключив доминируемые стратегии.

Решение. Для игрока 1: вторая стратегия (строка 2 матрицы) доминирует четвертую и шестую стратегии, поэтому четвертую и шестую строки можно вычеркнуть. Для игрока 2: третья стратегия (столбец 3) доминирует четвертую, поэтому четвертый столбец можно вычеркнуть, и т.д.

Результирующая матрица имеет вид

Стратегии игрока 2     Стратегии игрока 1
	-8

Пример 6[1]. Как завоевать рынок?

Два конкурирующих друг с другом предприятия, выпускающие стиральные машины, имеют следующие доли общего сбыта своей продукции на местном рынке: 53% — предприятие 1 и 47% — предприятие 2.

Оба предприятия пытаются увеличить объем своих продаж. Для этого у них есть следующие альтернативы: а1 (b1) — расширить сеть сбыта; а2 (b2) — рекламировать свою продукцию; а3 (b3) — увеличить ассортимент (число моделей стиральных машин); а4 (b4) — ничего не предпринимать.

Анализ показал, что при осуществлении обоими предприяти­ями указанных мероприятий доля (в %) предприятия 1 на рынке стиральных машин изменится следующим образом:

Стратегии предприятия 2     Стратегии предприятия 1	b1	b2	b3	b4
а1	-4	-5	-1
а2	-1		-3
а3	-3		-5
а4	-8	-7	-6

Сформулируйте данную ситуацию в виде игры.

Вопросы:

Какое из мероприятий предприятия 1 наиболее эффективно?

Какую долю на рынке будет иметь предприятие 1?

Какое из мероприятий предприятия 2 наиболее эффективно?

С какой частотой следует предприятию 2 использовать стра­
тегию «реклама»?

Решение. Приведенную выше таблицу можно рассматривать как платежную матрицу игры двух лиц с нулевой суммой. Альтер­нативы, имеющиеся в распоряжении предприятий, — стратегии игроков. Прежде всего следует исключить доминируемые страте­гии игроков: а4 игрока 1 и Ь4 игрока 2. В результате получим

Стратегии предприятия 2     Стратегии предприятия 1	b1	b2	b3
а1	-4	-5	-1
а2	-1		-3
а3	-3		-5

Увеличив все элементы матрицы на 6, решим следующую за­дачу линейного программирования:

t1 + t2+t3 min

2t1 +5t2+3t3 1

t1 +6t2+7t3 1

5t1 +3t2+t3 1,

Используя надстройку Поиск решения ППП EXEL, получаем решение задачи линейного программирования t1*=0,105, t2*=0,158, t3*=0.

Оптимальное значение целевой функции равно 0,26. Решение двойственной задачи имеет вид u1*=0,105 u2*=0, u3*= 0,158. Переходя к переменным исходной задачи и учитывая, что цена игры v равна v = 1/(t1* + t2*+t3 *) = 3,85 и вероятность xi i-ой чистой стратегии равна xi = ti* v, получаем:

x1 = 0,4, x2 = 0,6, x3 = 0, x4 = 0.

Цена игры, соответствующая первоначальной мат­рице, равна -2,15 (3,85 - 6). Таким образом, предприятие 1 при многократном повторении игры должно использовать с частотой 0,4 стратегию а1 (расширить сеть сбыта), с частотой 0,6 — страте­гию а2 (рекламировать свою продукцию), а стратегии а3 (увели­чить ассортимент) и а4 (ничего не предпринимать) не использо­вать вовсе. При этом доля сбыта предприятия на рынке уменьшит­ся на 2,15%. Оптимальная смешанная стратегия предприятия 2: с частотой 0,4 использовать стратегию b1 (расширить сеть сбыта) и с частотой 0,6 — стратегию b3 (увеличить ассортимент). Страте­гии b2 (рекламировать свою продукцию) и b4 (ничего не делать) не применять вовсе. Доля предприятия 2 на рынке увеличится на 2,15%. Казалось бы, поскольку в результате осуществления своих мероприятий предприятие 1 «теряет рынок», ему не следует ни­чего предпринимать, однако в этом случае оно потеряет еще боль­ше (в соответствии со стратегией а 4) из-за действий предприятия 2, которому они выгодны.

Ответы: 1. Реклама. 2. 50,85%.

Увеличение ассортимента.

С нулевой частотой, т.е. стратегия «реклама» предприятием­
2 вообще не должна применяться.

Контрольные вопросы и задания

Вопросы

1. Как определить нижнюю и верхнюю цену матричной игры
и какое соотношение существует между ними?

2. Сформулируйте основную теорему теории матричных игр.

3. Какие существуют методы упрощения игр?

4. На чем основана связь матричной игры и задачи линейного
программирования?

Тесты

Вопрос 1. Нижняя цена матричной игры определяется следующей формулой:

1)

2)

3)

4)

5)

Вопрос 2. Верхняя цена матричной игры определяется следующей формулой:

1)

2)

3)

4)

5)

Вопрос З. Какова верхняя цена следующей игры?

Стратегии игрока 2     Стратегии игрока 1
		-4
	-4
		-6

Варианты ответов:

1)1; 2)3; 3)4; 4)5; 5)6.

Вопрос 4. Какова нижняя и верхняя цена игры для нижепри­веденной матрицы?

Стратегии игрока 2     Стратегии игрока 1
			-3	-1
					-2
				-4

Варианты ответов:

1) (-4,10); 2) (0,5); 3) (2,4); 4) (3,5); 5) (2,8).

Вопрос 5. Чему равно значение элемента матрицы игры в сед-ловой точке?

Стратегии игрока 2     Стратегии игрока 1
		-5

Варианты ответов:

1) 6; 2) 8; 3) 15; 4) 25; 5) седловая точка отсутствует.

Вопрос 6. Используя свойство доминирования стратегий игро­ков, максимально редуцируйте следующую матрицу игры:

Стратегии игрока 2     Стратегии игрока 1

Какова размерность результирующей матрицы?

Варианты ответов:

1) 1 х 2; 2) 2 х 1; 3) 2 х 2; 4) 3 х 2; 5) 3 х 3.

Вопрос 7. Найдите цену следующей игры

Стратегии игрока 2     Стратегии игрока 1

Варианты ответов:

1)1; 2)1,5; 3)2; 4)2,5; 5)3.

Вопрос 8. Два игрока одновременно и независимо показывают 0,1, 2 или 3 пальца. Игрок, показавший большее число пальцев, платит другому игроку сумму, равную разности чисел пальцев, показанных им и его соперником. Какова цена такой игры?

Варианты ответов:

1)3; 2)2; 3)1; 4)0; 5)-1.

Вопрос 9. Два игрока одновременно и независимо показывают 1,2 или 3 пальца. Пусть s — сумма чисел пальцев, показанных обо­ими противниками. Если s — нечетное, то игрок 1 платит друго­му игроку сумму s, если же s — четное, эту сумму выплачивает иг­рок 2. Чему равна цена такой игры?

Варианты ответов:

1)-1; 2)0; 3)1; 4)1,3; 5)1,7.

Вопрос 10. Постройте платежную матрицу следующей игры.

Игрок 2 прячет в одном из n мест предмет стоимостью сj (j=1,2,…,n). Игрок 1 ищет этот предмет в одном из n мест, и если находит, то получает сj, в противном случае получает 0. Пусть n=4 и вектор стоимости предметов с = (5, 7, 3, 12). Чему равна цена игры?

Варианты ответов:

1)1,75; 2)1,57; 3)1,32; 4)1,23; 5)1,12.

Задание 3.1. В задачах 3.1.1 – 3.1.10 найдите решение игр, определяемых следующими платёжными матрицами:

3.1.1 3.1.2 3.1.3 3.1.4 3.1.5

3.1.6 3.1.7 3.1.8 3.1.9 3.1.10

Задание 3.2.

Задача 3.2.1. По требованию рабочих некоторой компании проф­союз ведет с ее руководством переговоры об организации горячих обедов за счет компании. Профсоюз, представляющий интересы рабочих, добивается того, чтобы обед был как можно более качест­венным и, следовательно, более дорогим. Руководство компании имеет противоположные интересы. В конце концов стороны до­говорились о следующем. Профсоюз выбирает одну из шести фирм (Ф1,…,Ф6), поставляющих горячее питание, а руководство компании — набор блюд из семи возможных вариантов (B1,…,B7). После подписания соглашения профсоюз формирует следующую платежную матрицу, элементы которой представляют стоимость набора блюд:

Вариант Фирма   Ф	B1	B2	B3	B4	B5	B6	B7
Ф1	2,3	4,3	3,3	2,8	5,2	2,9	3,3
Ф2	4,2	2,2	2,7	4,2	2,2	3,7	2,7
Ф3	1,2	3,7	2,7	5,2	1,2	1,7	3,7
Ф4	4,2	1,7	2,2	1,4	2,9	3,2	1,2
Ф5	3,2	3,2	2,9	2,2	6,2	2,4	1,7
Ф6	1,7	4,2	2,5	3,2	4,7	2,7	2.0

Определите оптимальные стратегии игроков и цену игры.

Вопросы:

Чему равна цена игры?

Какая фирма наиболее предпочтительна для профсоюза?

Какой набор руководство компании считает наиболее «вы­
годным»?

Чему равна нижняя цена игры?

- Задача 3.2.2. Две телевизионные компании (А и В) планируют к размещению в эфире по две передачи (новостную и спортивную). Новости компании А долее популярны, чем новости компании В, но компания В готовит лучшие спортивные передачи. Опросы показали, что если А и В одновременно размещают новостную программу, то доля аудитории составит 55% к 45% соответственно, если обе компании демонстрируют спортивную программу, то доля аудитории составит 44% к 56%. Если А показывает спорт в то время, как В – новости, доля аудитории каждой компании – 50%. Если А показывает новости, а В – спортивные репортажи, доля аудитории составит 52% к 48%. Решите игру. Как изменится решение при других соотношениях аудитории компаний?

- Задача 3.2.3. Фирма, занимающаяся производством и переработкой сельскохозяйственной продукции, может: 1) сразу предложить продукцию на рынок; 2) продавать после небольшого периода хранения; 3) продавать после дополнительной обработки. Потребители могут приобрести продукцию: 1) немедленно; 2) в течение небольшого периода времени; 3) в течение длительного периода времени. В зависимости от выбранных стратегий поведения на рынке и сложившейся конъюнктуры доход предприятия определяется следующей таблицей:

Выбор потребителя

Стратегия поведения

Определите оптимальные пропорции производства и переработки продукции.

Задача 3.2.4. Имеются два предприятия, которые в дополнение к основной продукции могут выпускать побочную продукцию од­ного и того же назначения — пластмассовые игрушки. Известно, что они могут продавать ее в одном и том же городе. Игрушки немного отличаются по конструкции, оформлению, удобству и т.д. Первое предприятие может выпускать игрушки типа A1, A2,…, Am; второе — типа B1, B2,… Bn. Себестоимость и цена игрушек у всех предприятий одинаковы. Всего в течение года продается N игрушек. Если первое предприятие выпускает игрушки типа Аi, а второе — типа Bj, то первое предприятие продаст rijN игрушек, а второе — (N— rijN). Каждое предприятие стремится получить максимальный доход от продажи игрушек.

Пусть m = 4, n = 5, N= 300 000, цена одной иг­рушки составляет 20 руб., элементы матрицы {rij }4;5 представле­ны в таблице:

Игрушки предприятия 2 Игрушки предприятия 1	B1	B2	B3	B4	B5
А1	0,2	0,7	0,4	0,8	0,3
А2	0,8	0,5	0,1	0,3	0,7
А3	0,4	0,6	0,9	0,5	0,6
А4	0,7	0,3	0,5	0,3	0,5

Сформулируйте игру двух лиц, считая игроком 1 первое пред­приятие. Определите выигрыш (доход от продажи) каждого пред­приятия.

Вопросы:

Каков общий средний доход первого предприятия?

Каков общий средний доход второго предприятия?

Какое изделие следует выпускать первому предприятию
с наибольшей вероятностью?

Какое изделие следует выпускать "второму предприятию
с наибольшей вероятностью?

Какова частота применения стратегии «Выпускать изделие B2»?

Задача 3.2.5. Завод выпускает скоропортящуюся продукцию, которую может:

А1 – сразу отправить потребителю;

А2 – отправить на склад для хранения;

А3 – подвергнуть дополнительной обработке для длительного хранения.

Потребитель, в свою очередь, может приобрести продукцию:

В1 – немедленно;

В2 – в течение небольшого периода;

В3 – после длительного периода времени.

В случае стратегий А2 и А3 завод несет дополнительные затраты на хранение и обработку продукции, которые не требуются для А1. Однако при А2 следует учесть возможные убытки из-за порчи продукции, если потребитель выберет стратегии В2 или В3. Матрица затрат представлена в таблице:

Bj Ai	В1	В2	B3
A1
A2
A3

Вопросы: