Одиниці вимірювання величин молекулярної фізики

Концентрація молекул – величина, що дорівнює відношенню 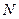кількості молекул до об'єму , який вони займають:

,

Молярна маса - входить у рівняння Клапейрона-Мендєлєєва:

,

де кількість молів речовини є масою моля речовини;

.

Універсальна газова стала – дорівнює відношенню роботи 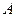здійснюваної ідеальним газом під час ізобаричного його нагрівання до інтервалу 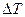температур і кількості молів речовини газу, що нагрівається.

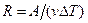, де ;

,

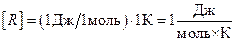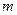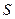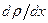Коефіцієнт дифузії – визначається з формули: де - маса газу, перенесеного за час через площадку ; – градієнт густини.

Звідси одержуємо:

;

1 дорівнює коефіцієнту дифузії середовища, в якому через площадку в 1 перпендикулярно градієнту густини 1 переноситься за 1 с речовина масою 1 кг.

Динамічна в’язкість (коефіцієнт в’язкості). На основі молекулярно-кінетичної теорії виведено наступну формулу динамічної в’язкості:

.

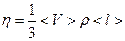тут - густина газу, - середня швидкість хаотичного руху молекул, - середня довжина вільного пробігу молекул.

Тоді: 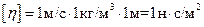(паскаль – секунда ).

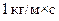Градієнт температури (векторна величина) – швидкість зміни температури в деякому напрямку:

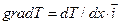, де - одиничний вектор уздовж осі . Під час рівномірного розподілу температури в напрямку градієнту:

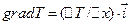
Отже .

Температурний коефіцієнт лінійного розширення 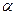- це відношення відносного лінійного видовження тіла до зміни температури, що викликала це видовження: , якщо в інтервалі , то Звідси .

Температурний коефіцієнт об’ємного розширення визначається з співвідношення: 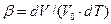. Якщо в інтервалі , то , звідси .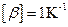

Питома теплоємність – кількість теплоти, необхідна для нагрівання одиниці маси тіла на один кельвін:

, отже .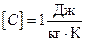

Теплопровідність - величина, що чисельно дорівнює відношенню кількості теплоти, перенесеної через одиничну плоску поверхню, нормальну до вектора градієнта температури, за 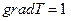, до часу, протягом якого ця теплота перенесена. З рівняння теплопровідності:

, ;

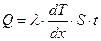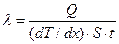звідси

Поверхневий натяг 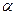- величина, що дорівнює відношенню сили , що діє на ділянці контура поверхні рідини до довжини цієї ділянки: , .