 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Виды деформаций стержня и связанные с ними геометрические характеристики поперечных сечений
|
|
Тема №1
Геометрические характеристики поперечных сечений стержня.
Лекция №1
Виды деформаций стержня и связанные с ними геометрические характеристики поперечных сечений
При расчетах элементов конструкций используются различные геометрические характеристики поперечных сечений.
Так, например, при центральном сжатии стержня силой  (рис.1.1) используется площадь поперечного сечения -
(рис.1.1) используется площадь поперечного сечения -  . Она применяется при определении напряжений
. Она применяется при определении напряжений  и деформаций
и деформаций  стержня.
стержня.

Рис. 1.1 Центральное сжатие стержня
Стержни могут иметь различную форму поперечных сечений: круг, прямоугольник, тавр, уголок, швеллер, двутавр и др. При работе стержня на сжатие, сжимающую силу желательно прикладывать в центре тяжести сечения (рис.1.1). Координаты центра тяжести плоской фигуры (поперечного сечения стержня) определяются по формулам известным из курса теоретической механики:
 , ,
|  . .
| (1.1) |
В формулах (1.1)  и
и  - статические моменты поперечного сечения относительно осей
- статические моменты поперечного сечения относительно осей 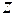 и
и  соответственно.
соответственно.
В случае работы стержня на изгиб (рис.1.2) необходимо использовать более сложные геометрические характеристики: момент инерции сечения относительно оси 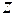 ; момент инерции сечения относительно оси
; момент инерции сечения относительно оси  ; центробежный момент инерции сечения относительно осей
; центробежный момент инерции сечения относительно осей  (
( ,
,  ,
,  ).
).

Рис. 1.2 Изгиб стержня
Эти геометрические характеристики входят в формулы для вычисления напряжений  и перемещений
и перемещений  .
.
При работе стержня на кручение (рис.1.3) используется геометрическая характеристика поперечного сечения стержня полярный момент инерции 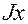 (
( ).
).

Рис. 1.3 Кручение стержня
Эта геометрическая характеристика входит в формулы для вычисления касательных напряжений  и углов закручивания (перемещений)
и углов закручивания (перемещений) 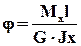 .
.
Дадим определение геометрических характеристик через интегралы по площади.
1.2 Площадь, статические моменты и центр тяжести.
Рассмотрим поперечное сечение стержня произвольной формы площадью  (рис.1.4). Обозначим через
(рис.1.4). Обозначим через  точку с координатами
точку с координатами 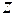 ,
,  . В окрестности точки выделим элементарную площадку площадью
. В окрестности точки выделим элементарную площадку площадью  .
.

Рис. 1.4
Сумма элементарных площадей  по всему сечению называется площадью
по всему сечению называется площадью  (рис. 1.4).
(рис. 1.4).
Статическим моментом сечения относительно оси 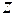 (
( ) называется сумма (по всему сечению) произведений элементарных площадей
) называется сумма (по всему сечению) произведений элементарных площадей  на координату
на координату  (рис. 1.4).
(рис. 1.4).
Статическим моментом сечения относительно оси  (
( ) называется сумма (по всему сечению) произведений элементарных площадей
) называется сумма (по всему сечению) произведений элементарных площадей  на координату
на координату 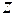 (рис. 1.4).
(рис. 1.4).
Таким образом, площадь и статические моменты сечения относительно осей 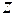 ,
,  определяются через интегралы по площади:
определяются через интегралы по площади:
 , ,
|  , ,
|  . .
| (1.2) |
Площадь и статические моменты сечения можно вычислять, используя обычные интегралы. Рассмотрим плоскую фигуру ограниченную функцией  на отрезке
на отрезке  (рис.1.5)
(рис.1.5)
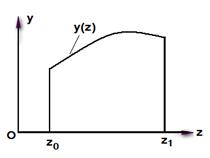
Рис. 1.5 Плоская фигура, ограниченная кривой  на
на 
Из курса высшей математики известно, что площадь и статические моменты определяются по формулам:

| 
| 
| (1.3) |
При параллельном переносе осей статические моменты меняются и могут принимать положительные или отрицательные значения, а также быть равными нулю. Ось, проходящая через центр тяжести, называется центральной. Статический момент сечения относительно центральной оси равен нулю. Ось симметрии фигуры является центральной осью.
Из формул (1.1) следует

| 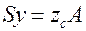 . .
| (1.4) |
Статический момент относительно оси 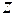 (
( ) равен произведению всей площади сечения
) равен произведению всей площади сечения  на координату
на координату  ее центра тяжести.
ее центра тяжести.
Статический момент относительно оси  (
( ) равен произведению всей площади сечения
) равен произведению всей площади сечения  на координату
на координату  ее центра тяжести (рис.1.4).
ее центра тяжести (рис.1.4).
Рассмотрим простейшие примеры определения площади, статических моментов и положения центра тяжести сечения.
Пример 1.1 Найти площадь прямоугольника (рис.1.6)
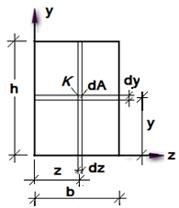
Рис. 1.6 Прямоугольник
Зафиксируем произвольную точку  прямоугольника координатами
прямоугольника координатами 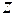 ,
,  . Вблизи точки
. Вблизи точки  выделим элементарную площадку площадью
выделим элементарную площадку площадью 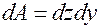 . Площадь элементарной горизонтальной полоски равна
. Площадь элементарной горизонтальной полоски равна  . Тогда площадь прямоугольника равна сумме по высоте сечения площадей элементарных горизонтальных полосок, т.е.
. Тогда площадь прямоугольника равна сумме по высоте сечения площадей элементарных горизонтальных полосок, т.е.  .
.
Проведем аналогичные вычисления, используя обычный определенный интеграл (1.3) В данном случае  ,
,  ,
,  . Тогда
. Тогда  .
.
Пример 1.2 Найдем координаты центра тяжести прямоугольного треугольника 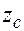 ,
, 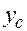 (рис.1.7). Используем формулы (1.3) для
(рис.1.7). Используем формулы (1.3) для  и
и  .
.
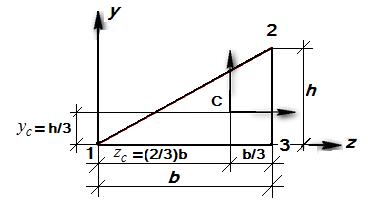
Рис. 1.7Прямоугольный треугольник
Уравнение прямой  . Отрезок интегрирования
. Отрезок интегрирования  ,
,  . Площадь
. Площадь  . Статические моменты
. Статические моменты  ,
,
 .
.
Координаты центра тяжести: 
 ;
;  .
.
Таким образом, центр тяжести в прямоугольном треугольнике удален от вершины прямого угла на 1/3 длин катетов.
Из курса аналитической геометрии известно, что координаты центра тяжести произвольного треугольника определяются через координаты вершин треугольника по формулам:
 , ,
|  . .
| ( ) )
|
Например, для треугольника (рис.1.7) получим:
 ;
;  .
.
Пример 1.3 Найдем координату центра тяжести полукруга 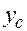 (рис.1.8). Используем формулу (1.3) для
(рис.1.8). Используем формулу (1.3) для  .
.
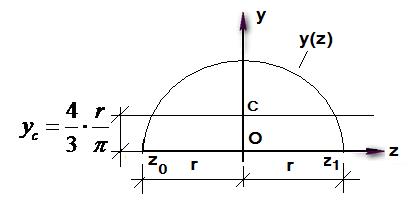
Рис. 1.8 Полукруг
Уравнение дуги полуокружности 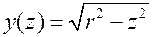 ,
,  ,
,  . Статический момент равен
. Статический момент равен  ,
,
 . Следовательно,
. Следовательно,  .
.
Статические моменты сложного сечения, разбитого на простейшие части (рис.1.9,a), для которых известны площади  и положение центра тяжести
и положение центра тяжести  ,
,  определяются по формулам:
определяются по формулам:
 , ,
|  . .
| (1.5) |
Пример 1.4 Определим центр тяжести сложного сечения, состоящего из двух фигур (рис.1.9,а).
Начало координат примем в т.О. Исходную фигуру разобьем на две простые: прямоугольник и треугольник. Площадь прямоугольника и его координаты центра тяжести:  ;
; 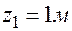 ;
;  . Площадь треугольника и его координаты центра тяжести:
. Площадь треугольника и его координаты центра тяжести:  ;
;  ;
;  .
.
Площадь сложной фигуры 
Статические моменты:  ;
;
 .
.
Координаты центра тяжести:  ;
;  . Центральные оси сложной фигуры показаны на рис. 1.9,б.
. Центральные оси сложной фигуры показаны на рис. 1.9,б.
Сделаем проверку найденных координат центра тяжести. Статические моменты относительно центральных осей равны нулю ( ,
,  ).
).
Вычислим координаты центров тяжести прямоугольника и треугольника относительно центральных осей всей фигуры:  ;
;  ;
;
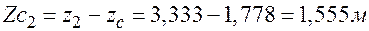 ;
;  ;
;

| 
|
Рис. 1.9 Сложное сечение из двух фигур
 ;
;
 .
.
Координаты центров тяжести определены верно (погрешность соответствует правилу округления, применяемому при вычислениях).
1.3 Моменты инерции сечений.
Осевым моментом инерции сечения относительно данной оси называется сумма по всему сечению произведений элементарных площадей  на квадрат их расстояний до данной оси (рис.1.10). Таким образом,
на квадрат их расстояний до данной оси (рис.1.10). Таким образом,

| 
| (1.6) |
Полярным моментом инерции сечения относительно данной точки (полюс О) называется сумма по всему сечению произведений элементарных площадей  на квадрат их расстояний до этой точки (рис.1.10) .. Следовательно,
на квадрат их расстояний до этой точки (рис.1.10) .. Следовательно,

| (1.7) |
Осевые и полярный моменты инерции всегда положительны и выражаются в  или
или  .
.
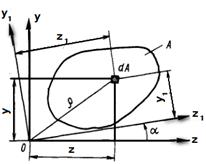
Рис. 1.10 К определению моментов инерции
Отметим интересное свойство: полярный момент инерции  равен сумме осевых моментов инерции
равен сумме осевых моментов инерции  и
и  относительно любой пары взаимно перпендикулярных осей
относительно любой пары взаимно перпендикулярных осей 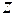 и
и  , проходящих через полюс О.
, проходящих через полюс О.
Действительно, как видно из рис.1.10, 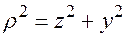 , и
, и
 .
.
Следовательно,
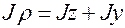 . .
| (1.8) |
Если оси 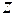 и
и  повернуть относительно полюса на угол
повернуть относительно полюса на угол  (рис.1.10), то
(рис.1.10), то  и, следовательно
и, следовательно 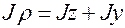 .
.
Таким образом, при любом повороте осей относительно начала координат сумма осевых моментов остается постоянной
 . .
| (1.10) |
Центробежным моментом инерции сечения относительно координатных осей  , называется сумма по всему сечению произведений элементарных площадей
, называется сумма по всему сечению произведений элементарных площадей  на их координаты
на их координаты  (рис.1.10).
(рис.1.10).
Таким образом,

| (1.11) |
Центробежный момент инерции  выражается в
выражается в  или
или  и может быть положительным, отрицательным и равным нулю в зависимости от положения относительно координатных осей.
и может быть положительным, отрицательным и равным нулю в зависимости от положения относительно координатных осей.
На рис.1.11 показано четыре различных положения прямоугольного треугольника относительно центральных осей  .
.

Рис. 11К определению знака центробежного момента инерции
Центробежный момент инерции  , если сумма площадей треугольника отмеченных знаком плюс (четверти где
, если сумма площадей треугольника отмеченных знаком плюс (четверти где  ) больше чем сумма площадей отмеченных знаком минус.
) больше чем сумма площадей отмеченных знаком минус.
Из последних рассуждений следует, что если одна из осей 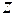 или
или  является осью симметрии сечения, то
является осью симметрии сечения, то  (рис. 1.12).
(рис. 1.12).

Рис. 1.12 Центробежный момент для симметричных сечений 
Если поперечное сечение задается как плоская фигура, ограниченная кривой  на отрезке
на отрезке  (рис.1.5), то осевые и центробежный моменты инерции определяются по формулам:
(рис.1.5), то осевые и центробежный моменты инерции определяются по формулам:

| 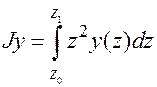
| 
| (1.12) |
Пример 1.5 Определить моменты инерции прямоугольного сечения относительно центральных осей (рис.1.13).
Разобьем прямоугольник на элементарные горизонтальные полоски площадью  . Элементарный момент инерции горизонтальной полоски относительно оси
. Элементарный момент инерции горизонтальной полоски относительно оси 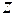 равен
равен  . Для вычисления момента инерции прямоугольника необходимо просуммировать элементарные моменты полосок по высоте сечения
. Для вычисления момента инерции прямоугольника необходимо просуммировать элементарные моменты полосок по высоте сечения
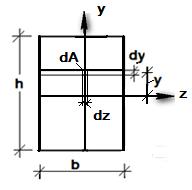
Рис. 1.13 К примеру 1.5
 . Аналогично
. Аналогично  .
.
Дата публикования: 2015-09-17; Прочитано: 1117 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
