Окружность. Общее уравнение окружности с центром в ( ) и радиусом имеет вид:

Общее уравнение окружности с центром в () и радиусом имеет вид:

Это уравнение может быть упрощено для частных случаев, например

является уравнением, определяющим окружность с центром в полюсе и радиусом .^[15]

Прямая

Радиальные прямые (те, которые проходят через полюс) определяются уравнением

где — угол, на который прямая отклоняется от полярной оси, то есть, где — наклон прямой в прямоугольной системе координат. Нерадиальная прямая, перпендикулярно пересекает радиальную прямую в точке определяется уравнением

Параметрические уравнения линии

Уравнения вида (1.19) Называются параметрическими уравнениями линии, если при изменении В некотором промежутке формулы (1.19) дают координаты любой точки данной линии и только таких точек. Если линия задана уравнением В полярных координатах, то ее пара Метрические уравнения можно записать так: (1.20) В уравнениях (1.20) роль параметра играет полярный угол

3. Кривые 2-го порядка. Уравнение эллипса, гиперболы, параболы.

Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида

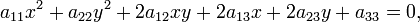
в котором по крайней мере один из коэффициентов отличен от нуля.