Уравнение прямой с угловым коэффициентом. Уравнение прямой вида , где x и y - переменные, а k и b – некоторые действительные числа, называется уравнением прямой с угловым коэффициентом (k – угловой

Уравнение прямой вида , где x и y - переменные, а k и b – некоторые действительные числа, называется уравнением прямой с угловым коэффициентом (k – угловой коэффициент). Уравнения прямой с угловым коэффициентом нам хорошо известны из курса алгебры средней школы. Такой вид уравнения прямой очень удобен для исследования, так как переменная y представляет собой явную функцию аргумента x.

Определение углового коэффициента прямой дается через определение угла наклона прямой к положительному направлению оси Ox.

Определение.

Углом наклона прямой к положительному направлению оси абсцисс в данной прямоугольной декартовой системе координат Oxy называют угол 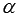, отсчитываемый от положительного направления оси Ох до данной прямой против хода часовой стрелки.

Если прямая параллельна оси абсцисс или совпадает с ней, то угол ее наклона считают равным нулю.

Определение.

Угловой коэффициент прямой есть тангенс угла наклона этой прямой, то есть, .

Если прямая параллельна оси ординат, то угловой коэффициент обращается в бесконечность (в этом случае также говорят, что угловой коэффициент не существует). Другими словами, мы не можем написать уравнение прямой с угловым коэффициентом для прямой, параллельной оси Oy или совпадающей с ней.