 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Индивидуальная домашняя контрольная работа №2
|
|
При выполнении задания используются задачники
1) Беклемишева Л.А., ПетровичА.Ю., ЧубаровИ.А. Сборник задач по аналитической геометрии и линейной алгебре, М., 1987 (при выполнении вариантов 1 -11)
2) Клетеник Д.В. Сборник задач по аналитической геометрии М., 1975 (при выполнении вариантов 12-25).
| В1 | 1.4 | 2.39 | 3.21 | 5.9(2) | 5.39(3) | 6.17(5) | 6.39 | 6.45(2) |
| В2 | 1.14 | 3.4 | 3.22(1) | 5.10(3) | 5.41 | 6.23(2) | 6.32(2) | 6.47(2) |
| ВЗ | 1.15 | 3.6 | 3.22(2) | 5.11 | 5.42 | 6.24 | 6.29 | 6.49 |
| В4 | 2.14(1) | 3.8 | 3.23(1) | 5.12 | 5.50 | 6.18(2) | 6,44(3) | 6.53 |
| В5 | 2.14(2) | 3.10 | 3.23(2) | 5.15 | 5.48 | 6.25(2) | 6.28 | 6.61(2) |
| В6 | 2.14(3) | 3.12 | 3.25(1) | 5.16 | 5.43 | 6.18(4) | 6.33 | 6.64 |
| В7 | 2.26(1) | 3.15 | 3.25(2) | 5.17 | 5.52 | 6.23(4) | 6.35(1) | 6.65 |
| В8 | 2.25 | 3.18 | 3.26(1) | 5.18 | 5.47 | 6.19(2) | 6.27(2) | 6.69 |
| В9 | 2.26(2) | 3.21 | 3.26(2) | 5.20 | 5.40 | 6.20(2) | 6.35(2) | 6.70(1) |
| В10 | 2.35 | 3.20(1) | 3.26(30 | 5.22(3) | 5.37 | 6,21(3) | 6.27(4) | 6.70(2) |
| В11 | 2.36 | 3.20(2) | 3.26(4) | 5.22(5) | 5.36 | 6.22 | 6.44(4) | 6.71(1) |
| В12 | 874(1) | 1163(1) | ||||||
| В.13 | 874(1) | 1063(2) | 1020(2) | |||||
| В.14 | ||||||||
| В.15 | ||||||||
| В.16 | 874(2) | 1020(1) | ||||||
| В.17 | 1019(в) | |||||||
| В.18 | 1063,а | |||||||
| В.19 | 1063,6 | |||||||
| В.20 | 1О83,в | |||||||
| В.21 | ||||||||
| В.22 | 1063(3) | 1019,в | ||||||
| В23 | ||||||||
| В24 | ||||||||
| В25 |
Замечание: по данному заданию предусмотрено собеседование со студентами.
3.5. Примерные варианты контрольной работы по аналитической геометрии
Варианты № 1
1. Даны проекции вектора 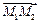 , на оси координат
, на оси координат 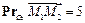 ,
, 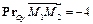 . Зная, что точка
. Зная, что точка 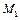 имеет координаты (-2,3), найти координаты точки
имеет координаты (-2,3), найти координаты точки 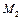 .
.
2. Сила 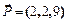 приложена к точке A(4,2,-3). Определить величину и направляющие косинусы момента этой силы относительно точки C(2,4,0).
приложена к точке A(4,2,-3). Определить величину и направляющие косинусы момента этой силы относительно точки C(2,4,0).
3. Составить уравнение плоскости, которая проходит через две точки 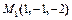 и
и 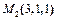 перпендикулярно к плоскости
перпендикулярно к плоскости 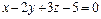 .
.
4. Составить уравнение гиперболы, если известны ее эксцентриситет 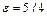 , фокус F(5,0) и уравнение соответствующей директрисы
, фокус F(5,0) и уравнение соответствующей директрисы 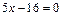 .
.
5. Определить вид поверхности 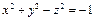 и установить, при каких значениях m плоскость
и установить, при каких значениях m плоскость 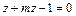 пересекает ее: а) по эллипсу, б) по гиперболе.
пересекает ее: а) по эллипсу, б) по гиперболе.
Вариант №2
1. Даны две точки P(-5,2), Q(3,1). Найти проекцию вектора 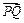 на ось, которая составляет с осью (Ох) угол
на ось, которая составляет с осью (Ох) угол 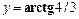 .
.
2. Даны три силы 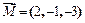 ,
, 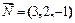 ,
, 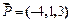 , приложенные к точке С (-1,4, -2). Определить величину и направляющие косинусы момента равнодействующей этих сил относительно точки
, приложенные к точке С (-1,4, -2). Определить величину и направляющие косинусы момента равнодействующей этих сил относительно точки
А (2,3,-1).
3. Составить уравнение прямой, которая проходит через точку М(-1, 2, -3) перпендикулярно вектору 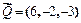 и пересекает прямую
и пересекает прямую 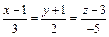 .
.
4. Составить уравнение эллипса, фокусы которого расположены на оси абсцисс, симметрично относительно начала координат, если дана точка 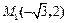 эллипса и расстояние между его директрисами равно 10.
эллипса и расстояние между его директрисами равно 10.
5. Определить вид поверхности 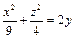 и ее сечения плоскостью
и ее сечения плоскостью 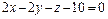 .
.
Вариант №3
1. Даны две точки A(3,-4,-2), B(2, 5,-2). Найти проекцию вектора 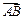 на ось, составляющую с координатными осями Ох и Оу; углы
на ось, составляющую с координатными осями Ох и Оу; углы 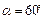 и
и 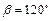 , а с осью Oz - тупой угол
, а с осью Oz - тупой угол 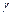 .
.
2. Даны три силы 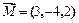 ,
, 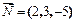 ,
, 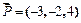 , приложенные к одной точке. Вычислить работу, которую производит равнодействующая этих сил, когда ее точка приложения, двигаясь прямолинейно, перемещается из положения
, приложенные к одной точке. Вычислить работу, которую производит равнодействующая этих сил, когда ее точка приложения, двигаясь прямолинейно, перемещается из положения 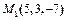 в положение
в положение 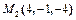 .
.
3. Составить уравнение плоскости, которая проходит через начало координат перпендикулярно двум плоскостям 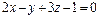 ,
, 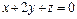 .
.
4. Составить уравнение параболы, если даны ее фокус 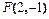 и директриса
и директриса 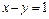 .
.
5. Определить вид поверхности 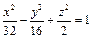 и вид ее сечения плоскостью
и вид ее сечения плоскостью 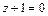 .
.
Дата публикования: 2015-07-22; Прочитано: 393 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
