 |
Главная Случайная страница Контакты | Мы поможем в написании вашей работы! | |
Тематические тесты алгебре и аналитической геометрии
|
|
Матрицы и определители
Тест1.
1. Единичная матрица – это квадратная матрица, у которой
1) все элементы равны 1;
2) все элементы первой строки равны 1;
3) все элементы, не стоящие на главной диагонали, равны 0;
4) все элементы главной диагонали равны 1, остальные равны 0;
5) все элементы либо нули, либо единицы.
2. Продолжите определение:
Треугольной матрицей называется матрица, все элементы которой, стоящие …… равны нулю.
3. Выбрать среди следующих утверждений верные утверждения:
1) любые две матрицы можно сложить;
2) любые две квадратные матрицы можно сложить;
3) любые две матрицы одинаковых размеров можно сложить;
4) любые две квадратные матрицы одного порядка можно сложить;
5) любую матрицу можно умножить на число;
6) при умножении матрицы на число 1 получится единичная матрица;
7) при умножении матрицы на число 0 получится нулевая матрица.
4. Дана матрица, имеющая размеры  . Транспонированная матрица имеет размеры
. Транспонированная матрица имеет размеры
1)  2)
2)  3)
3)  , 4)
, 4) 
5. Даны матрицы 

 . Какие из указанных пар можно сложить:1)
. Какие из указанных пар можно сложить:1)  , 2)
, 2)  , 3)
, 3)  , 4)
, 4)  , 5)
, 5)  , 6)
, 6) 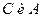 .
.
6. Если матрица А имеет размеры 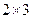 , матрица B – размеры
, матрица B – размеры  , матрица
, матрица
C – размеры  , то матрицы АC и BА имеют размеры
, то матрицы АC и BА имеют размеры
1)  и
и  ; 2)
; 2)  и
и 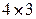 ; 3)
; 3)  и
и  ; 4)
; 4)  и
и  .
.
7. Даны матрицы  и
и  .
.
Какое из указанных произведений нельзя найти:
1)  2)
2)  3)
3)  4)
4)  5)
5) 
8. Пусть даны матрицы


 . Укажите произведения, которые можно найти: 1)
. Укажите произведения, которые можно найти: 1)  , 2)
, 2)  , 3)
, 3)  , 4)
, 4)  , 5)
, 5)  , 6)
, 6)  7)
7) 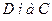 .
.
9. Если  – произвольная матрица и
– произвольная матрица и  – транспонированная к ней матрица, то 1)
– транспонированная к ней матрица, то 1)  .
.
2)  .
.
3)  .
.
4)  .
.
10. Пусть  и
и  существует. Укажите верные утверждения:
существует. Укажите верные утверждения:
1) 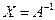 ; 2)
; 2) 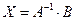 ; 3)
; 3)  ; 4)
; 4)  ; 5)
; 5) 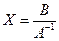 .
.
11. Ранг матрицы – это
1) число ненулевых элементов матрицы;
2) наибольший порядок ее миноров, отличных от нуля;
3) максимальное число линейно независимых строк матрицы;
4) число ненулевых миноров матрицы;
5) величина наибольшего ненулевого минора.
Тест2
1. Для матрицы B, полученной из квадратной матрицы n -го порядка А перестановкой местами i -ой строки и j -ой строки 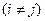
1)  2)
2)  ; 3)
; 3)  4)
4) 
2. Если А – квадратная матрица n -го порядка, то для транспонированной матрицы 
1)  2)
2)  ;
;
3) 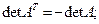 4)
4) 
5)
3. Пусть А квадратная матрица n -го порядка, а матрица B получена из транспонированной матрицы  перестановкой первого и последнего столбцов. Тогда
перестановкой первого и последнего столбцов. Тогда
1)  2)
2) 
3)  4)
4) 
4. Если  , где A – произвольная матрица второго порядка, E – единичная матрица, то
, где A – произвольная матрица второго порядка, E – единичная матрица, то
1)  .
.
2)  .
.
3)  .
.
4)  .
.
5. В квадратной матрице А n -го порядка i -ый столбец заменили на копию j -го столбца, оставив остальные столбцы неизменными. Определитель полученной матрицы равен
1)  2)
2)  3) 0 4)
3) 0 4) 
6. В квадратной матрице А строку умножим на число k (–1< k <0). Для полученной матрицы B:
1)  2)
2)  ; 3)
; 3)  4)
4) 
7. В квадратной матрице А i -ую строку заменили на сумму i -ой и j -ой строк ( . Для полученной матрицы B
. Для полученной матрицы B
1)  ; 2)
; 2)  ; 3)
; 3)  4)
4)  .
.
8. В квадратной матрице А n -го порядка изменили знак каждого элемента i -ой строки на противоположный. Определитель полученной матрицы равен
1)  2)
2)  3)
3)  4)
4) 
9. В квадратной матрице А все элементы первой и последней строки умножили на число k  . Определитель полученной матрицы равен
. Определитель полученной матрицы равен
1)  ; 2)
; 2) 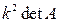 ; 3)
; 3)  ; 4)
; 4)  .
.
10. Для квадратной матрицы А сумма произведения элементов i -ой строки на их алгебраические дополнения равна
1) 0; 2)  3)
3)  4)
4) 
11. Если  – произвольная матрица, а
– произвольная матрица, а  , то
, то
1)  ; 2)
; 2)  ; 3)
; 3)  +1; 4)
+1; 4) 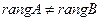 ;
;
5)  .
.
12. Определитель квадратной матрицы равен 0, если
1) элементы одной из строк пропорциональны элементам какого-нибудь столбца;
2) сумма всех элементов матрицы равна 0;
3) элементы, по крайней мере, двух строк пропорциональны;
4) произведение диагональных элементов равно 0.
13. Алгебраическое дополнение элемента  матрицы
матрицы  имеет вид:
имеет вид:
a)  ; b)
; b)  ; c)
; c)  ; d)
; d)  ;
;
14. Сумма произведений элементов какой-нибудь строки в определителе на алгебраические дополнения соответствующих элементов другой строки равна:
1) 1.
2) 0.
3) этому определителю.
4) другому определителю, отличному от 0.
15. Если А – треугольная матрица порядка n, то ее определитель равен
1) 0.
2) 1.
3) произведению диагональных элементов.
4) максимальному диагональному элементу.
Дата публикования: 2015-07-22; Прочитано: 705 | Нарушение авторского права страницы | Мы поможем в написании вашей работы!
