Тестовые задачи и сравнительная оценка алгоритмов

Всюду далее:

- точность решения по аргументам,

- точность решения по функции,

- число обусловленности , которое характеризует степень вытянутости линий уровня в окрестности . (Если 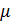велико, то линии уровня сильно вытянуты – функция имеет овражный характер, т.е. резко возрастает по одним направлениям и слабо меняется по другим [4, 5])

- число итераций,

- число вычислений функции,

- число аппроксимаций при наличии отрицательных собственных значений,

- число аппроксимаций при наличии нулевых собственных значений,

- число переходов к направлению отрицательной кривизны,

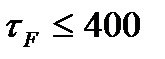() - число "правильных разрядов" , которые хотелось бы получить,

- характеризует степень однородности модельной квадратичной функции.

Задача 1 (функция Розенброка [14, задача 2], =2):

. Функция плохо обусловленная , не выпуклая, c параболическим оврагом, точка далека от точки .

Задача 2 (функция Пауэлла [14, задача 26], = 4):

,

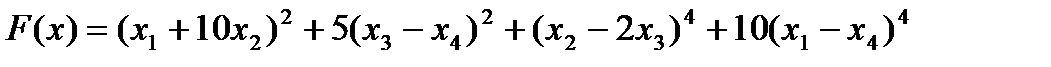. Функция не выпуклая, точка минимума - вырожденная .

Задача 3 (среднеквадратичная аппроксимация экспонентами [8], =4): ,

. Функция не выпуклая, с искривлённым оврагом, обусловленность велика.

Задача 4 (функция Вуда [14], =4):

, .

Задача содержит восемь предельных ограничений для значений, которые могут принимать независимые переменные, и характеризуется наличием неоптимальной стационарной точки при F (x) ≈ 8, обеспечивающей быструю сходимость. Функция имеет несколько локальных минимумов, это обстоятельство может вызвать преждевременное окончание процесса.

Задача 5 (функция Степенная, = 2):

.

В таблицах 1 – 5 приводятся результаты вычислений с помощью двух версий ньютоновского метода безусловной минимизации: «Mnb» и «MnbApp». «MnbApp» отличается от «Mnb» конечно-разностной аппроксимацией первых и вторых производных. Все версии алгоритмов написаны на языке Visual Basic.NET. В основе построения версий алгоритмов и формы представления таблиц 1 – 5 лежат работы [10, 11, 12, 13]. На рисунках 1 – 5 представлены скриншоты программы с результатами вычислений с помощью первой версии ньютоновского метода безусловной минимизации «Mnb».

В таблице 6 приведены результаты вычислений с помощью методов, описанных в монографии Поляка Б.Т. [8], краткое описание которых приводится ниже.

Метод Шора [6, 8, 15] «Шор-1» основан на эвристическом подборе матрицы преобразования пространства. Преобразования сводятся к последовательным растяжениям в специально подбираемых направлениях. Такие методы называют - алгоритмами. Они по структуре близки к квазиньютоновским методам переменной метрики, но основаны не на оценке матрицы вторых производных, а на построении матрицы преобразования, определяющей возврат от некоторых новых координат к исходным координатам.

Метод Дэвидона - Флетчера - Пауэлла «ДФП» [1, 2, 8] и метод Бройдена - Флетчера – Шенно «БФШ» [8] относятся к классу методов переменной метрики, называемых также квазиньютоновскими или градиентными с большим шагом. В этих методах в процессе поиска осуществляется аппроксимация матрицы вторых производных или обратной к ней. Причем для этого используются только первые производные. В методе «ДФП» направление градиента является отклоненным в результате умножения на положительно определенную симметрическую матрицу, обратную матрице вторых производных. На следующем шаге такая матрица представляется в виде суммы предыдущей и двух симметрических матриц ранга один каждая. Метод «БФШ» отличается от метода «ДФП» формулой пересчета положительно определенной симметрической матрицы, обратной матрице вторых производных.

Метод барицентрических координат «Барицентр» [8] относится к классу методов прямого поиска. В их основе лежит анализ определенного набора точек вокруг текущей точки, причем ищется такая точка, в которой значение целевой функции меньше, чем значение в текущей точке. Методы прямого поиска для решения задач оптимизации можно использовать тогда, когда отсутствует какая-либо информация о дифференцируемости целевой функции или для случая прерывистой функции.

Метод Пауэлла «Пауэлл» [3, 8, 14] использует значения функции в определенных точках для аппроксимации функции полиномом второй степени. Таким образом, предполагается, что в ограниченном интервале можно аппроксимировать функцию квадратичным полиномом, а затем использовать построенную аппроксимационную схему для оценивания координаты точки истинного минимума функции.

Разностный аналог градиентного метода «Градиент» [8] относится к классу методов прямого поиска, стратегия которого заключается в использовании значений функции для конечно-разностной аппроксимации первых производных.

Метод «Конград-2» [8] есть версия метода сопряженных направлений, а «Конград-3» является сочетанием метода сопряженных градиентов с методом переменной метрики [8, 9].

Метод «Симплекс» [8, 14] есть версия симплексного метода, идея которого состоит в сравнении значений функции в вершинах симплекса (правильный многогранник, имею­щий вершину) и перемещении в направлении оптимальной точки с помощью итерационной процедуры.

Таблица 1 - Сравнение предлагаемых методов для задачи 1

Метод
«Mnb»		2.5*10-24	1.5*10-12
«Mnb»		2.5*10-24	2*10-14
«Mnb»
«Mnb»
«Mnb»
«Mnb»
«Mnb»
«MnbApp»		8.8*10-20	2.9*10-10						-
«MnbApp»									-

Таблица 2 - Сравнение предлагаемых методов для задачи 2

Метод
«Mnb»		0	0
«MnbApp»									-

Таблица 3 - Сравнение предлагаемых методов для задачи 3

Метод
«MnbApp»		1.2*10-11	4*10-5						-
«MnbApp»		1.1*10-21	5*10-10						-
«MnbApp»		4.2*10-33							-

Таблица 4. - Сравнение предлагаемых методов для задачи 4

Метод
«Mnb»		7.8*10-21	7.6*10-11
«Mnb»		3.9*10-28	2*10-15
«Mnb»
«Mnb»
«Mnb»
«Mnb»
«Mnb»
«MnbApp»		7.7*10-15	9.8*10-8						-
«MnbApp»		3.2*10-22	3*10-11						-
«MnbApp»		1.7*10-26	4*10-14						-

Таблица 5. - Сравнение предлагаемых методов для задачи 5

Метод
«Mnb»		0	0
«Mnb»		0	0
«MnbApp»		6.6*10-8	3*10-2						-

Таблица 6. - Сравнение общеизвестных методов для задач 1-3

Метод
Задача 1
«Градиент»	-		2*10-6	10-9
«Симплекс»	-		-	10-8
«Барицентр»	-		10-9	10-17
«Конград-2»		-	10-5	10-9
«ДФП»		-	10-5	10-9
«БФШ»		-	10-6	10-11
«Шор-1»			10-7	10-15
Задача 2
«Симплекс»	-		-	7*10-8
«Барицентр»	-		10-4	10-18
«Конград-2»		-	10-2	10-4
«ДФП»		-	10-3	10-9
«БФШ»		-	10-3	10-9
«Шор-1»			10-6	10-13
Задача 3
«Конград-2»			10-4	10-13
«Конград-3»			10-8	10-18
«Шор-1»			10-7	6*10-5

Литература

1. Fletcher R., Powell M.J.D. A rapidly convergent descent method for minimization. – Comput. J., 1963.

2. Fletcher R., Reeves C. M. Function minimization by conjugate gradients. – Comput. J., 1964

3. Powell M.J.D. Computer J. 7, 155 (1964); 7, 303 (1965).

4. Гилл Ф., Мюррей У. Численные методы условной оптимизации. Изд.: «Мир». Москва, 1977.

5. Гилл Ф., Мюррей У., Райт М. Практическая оптимизация. Изд.: «Мир». Москва, 1985.

6. Ермольев Ю.М., Шор Н.З. О минимизации недифференцируемых функций. Кибернетика, 1967, № 1, с. 101-102.

7. Лачинов В.М., Поляков А.О. Информодинамика или путь к Миру открытых систем. СПб: Изд-во СПбГТУ, 1999.

8. Поляк Б.Т. Введение в оптимизацию. Изд.: «Наука», Москва. Главная редакция физико-математической литературы, 1983.

9. Поляк Б.Т. Метод сопряженных градиентов в задачах на экстремум. Журнал Вычислительной математики и математической физики, 1969, т. 9, № 4, с. 807-821.

10. Хакимов Б.Б., Маилян А.А., Маилян А.А., Хакимова А.Б. Патент на полезную модель №51252. Система для обработки данных и управления рынка. Зарегистрировано 27 января 2006. Москва.

11. Хакимова А.Б., Хакимов Б.Б. Единый подход к решению задач математического программирования гуманитарной компьютерной клиники. Материалы I международной конференции «Системные, информационные и технические средства и технологии в профессиональной деятельности, образовании, оздоровлении и профилактике». СПб: Изд-во СПбГТУ, 2003

12. Хакимова А.Б., Дикусар В.В., Зеленков Г.А. Увеличение эффективности ньютоновских методов оптимизации. Информдинамический подход. Труды ИСА РАН «Динамика неоднородных систем». Выпуск 14, Том 53. М.: Книжный дом «ЛИБРОКОМ», 2010. ISBN 978-5-397-00676-7

13. Хакимова А.Б., Зеленков Г.А. Увеличение эффективности ньютоновских методов минимизации. Вычисление длины шага. Труды ИСА РАН «Динамика неоднородных систем». Выпуск 14, Том 53. М.: Книжный дом «ЛИБРОКОМ», 2010. ISBN 978-5-397-00676-7

14. Химмельблау Д. Прикладное нелинейное программирование. Перевод с англ. И. М. Быховской и Б.Т. Вавилова. Изд.: «Мир», Москва 1975.

15. Шор Н.З. Методы минимизации недифференцируемых функций и их приложения. Киев: Наукова думка, 1979.